Akutantni trikotnik

Kaj so acutangulus trikotniki?

The Acutangulus trikotniki So tisti, katerih trije notranji koti so akutni koti; to pomeni, da je merilo vsakega od teh kotov manjše od 90 ° stopinj. Ker nimamo pravega kota, imamo, da teorem pitagore ni izpolnjen za to geometrijsko figuro.

Če želimo imeti kakšno vrsto informacij o kateri koli od njegovih strani ali kotov, je treba uporabiti druge teoreme, ki nam omogočajo dostop do teh podatkov. Tisti, ki jih lahko uporabimo, sta teorem dojk in kosinus.

Značilnosti akutantnega trikotnika

Med značilnostmi, ki jih ima ta geometrijska figura, lahko izpostavimo tiste, ki jih daje preprosto dejstvo, da je trikotnik. Med temi moramo:

- Trikotnik je poligon, ki ima tri strani in tri kote.

- Vsota njegovih treh notranjih kotov je enaka 180 °.

- Vsota dveh strani je vedno večja od tretjega.

Kot primer si oglejmo naslednji trikotnik ABC. Na splošno njihove strani identificiramo z malimi črkami in njihovimi koti z kapitalsko črko, tako da imata stran in njun nasprotni kot isto črko.

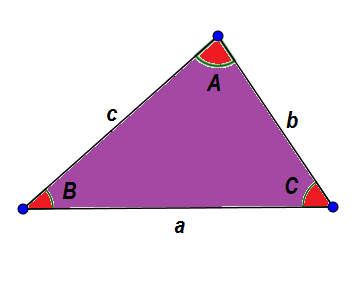
Zaradi že danih značilnosti to vemo:

A + b + c = 180 °

A + b> c, a + c> b in b + c> a

Glavna značilnost, ki razlikuje to vrsto trikotnika od ostalega, je, da so, kot smo že omenili, njegovi notranji koti akutni; to pomeni, da je merilo vsakega njegovega kota manjše od 90 °.

Trikotniki Acutangulus, skupaj z obljudnimi trikotniki (tisti, v katerih ima eden od njegovih zornih kotov, so mera, večji od 90 °), del poševnih trikotnikov. Ta komplet tvorijo trikotniki, ki niso pravokotniki.

Vam lahko služi: kakšni so elementi prispodobe? (Deli)

S tem, da smo del poševnih trikotnikov, moramo rešiti težave, pri katerih Acutangulus Triangles posreduje teorem dojk in kosinusa.

Teorem dojk

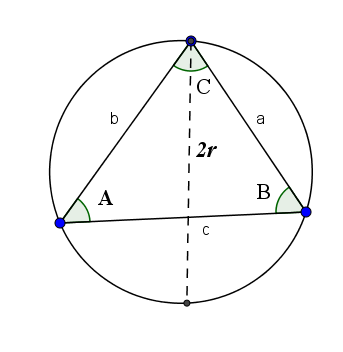
Teorem dojk potrjuje, da je razlog na eni strani s naročjem njegovega nasprotnega kota enak dvakratnemu polmeru kroga, ki ga tvorijo tri točke omenjenega trikotnika. To pomeni:

2r = a/sin (a) = b/sen (b) = c/sena (c)

Teorem Coseno

Po drugi strani nam Cosenov teorem daje te tri enakosti za vsak trikotnik ABC:

do²= b² + c² -2BC*cos (a)

b²= a² + c² -2ac*cos (b)

c²= a² + b² -2ab*cos (c)

Ti teoremi so znani tudi kot zakon sinusa in zakona kosina.

Druga značilnost, ki jo lahko damo akutangulozni trikotniki, je, da sta dva od njih enaka, če izpolnjujeta katero od naslednjih meril:

• Če imajo vse tri strani.
• Če imajo stran in dva kota enaka drug drugemu.
• Če imajo dve strani in enak kot.

Vrste trikotnikov Acutángulos

Trikotnike Acutangulus lahko razvrstimo glede na njihove strani. To bi lahko bilo:

Trikotniki enakostranični akutangulos

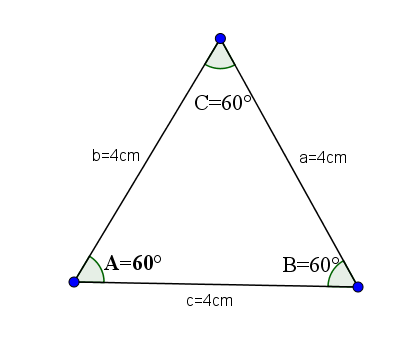
So akutangulozni trikotniki, ki imajo vse svoje enake strani in zato imajo vsi njihovi notranji koti enako vrednost, ki je a = b = c = 60 ° stopinj.

Kot primer, vzemimo naslednji trikotnik, katerih strani A, B in C imajo vrednost 4.

Isosceles acutángulos trikotniki

Ti trikotniki imajo poleg akutnih notranjih kotov značilno, da imajo dve enaki strani in tretji, ki se na splošno jemljejo kot osnova, drugačna.

Primer te vrste trikotnikov je lahko tisti, katerega baza je 3, drugi pa dve strani pa 5. S temi ukrepi bi imel kote, ki nasprotujejo enakim strani z vrednostjo 72,55 °, in nasprotni kot osnove bi bil 34,9 °.

Vam lahko služi: NULL kot: definicija in značilnosti, primeri, vaje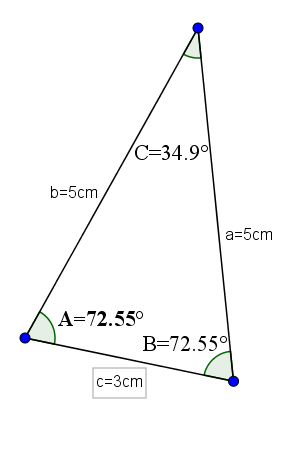

Scalene Acutangulus trikotniki

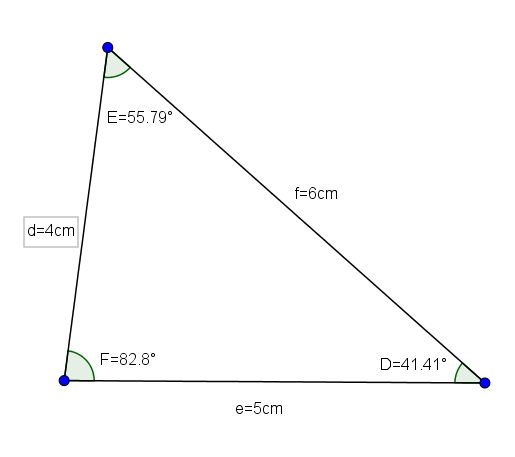
To so trikotniki, ki imajo vse svoje različne strani dve do dve. Zato so vsi njegovi koti, poleg manj kot 90 °.

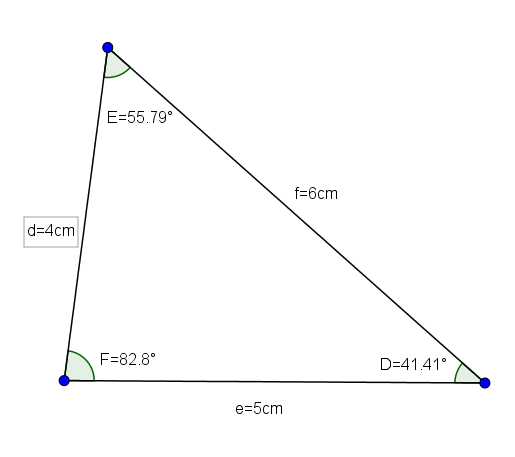
Trikotnik def (katerega ukrepi so d = 4, e = 5 in f = 6, njegovi koti pa so d = 41,41 °, e = 55,79 ° in F = 82,8 °.

Ločljivost trikotnikov Acutangles

Kot smo že povedali, za reševanje težav, pri katerih Acutangulus trikotniki posegajo.

Primer 1

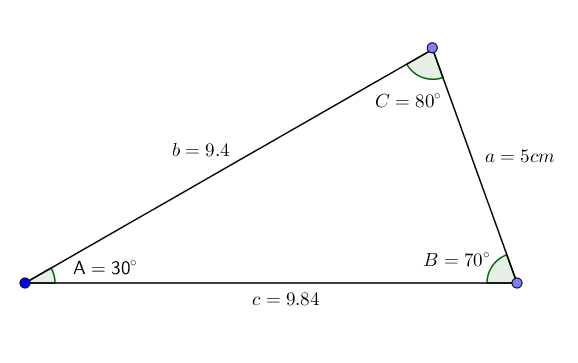
Glede na ABC trikotnik z koti A = 30 °, B = 70 ° in stran A = 5cm, želimo vedeti vrednost kota C in strani B in C.

Prva stvar, ki jo naredimo, je, da uporabimo dejstvo, da je vsota notranjih kotov trikotnika 180 °, da bi dosegli vrednost kota C.

180 ° = A + B + C = 30 ° + 70 ° + C = 100 ° + C

Očistimo C in imamo:

C = 180 ° - 100 ° = 80 °

Kot poznamo tri kote in eno stran, lahko uporabimo teorem dojk za določitev vrednosti preostalih strani. Za teorem moramo:

A/sin (a) = b/sen (b) in a/sen (a) = c/(sin (c)

Očistimo enačbo in moramo:

B = (a*sin (b))/sin (a) ≈ (5*0.940) / (0.5) ≈ 9.4

Zdaj moramo samo izračunati vrednost c. Nadaljujemo analogno kot v prejšnjem primeru:

C = (a*sin (c))/sin (a) ≈ (5*0.984)/(0.5) ≈ 9.84

Tako dobimo vse podatke trikotnika. Kot lahko opazimo, ta trikotnik vstopi v kategorijo skeniranja.

Primer 2

Glede na obrambni trikotnik s stranicami d = 4cm, e = 5cm in f = 6cm, želimo vedeti vrednost kotov omenjenega trikotnika.

V tem primeru bomo uporabili zakon o kosinusu, ki nam pove, da:

Vam lahko služi: vsota kvadratov dveh zaporednih številk

d²= e² + F² - 2efcos (d)

Iz te enačbe lahko razčistimo CO (D), kar ima za posledico:

Cos (d) = ((4)² - (5)² -(6)²)/(-2*5*6) = 0.75

Od tu moramo pristati 41.41 °

Z uporabo teorema Senoma imamo zdaj naslednjo enačbo:

D/(sin (d) = e/(sin (e)

Clealing Sen (E), moramo:

greh (e) = e*sen (d)/d = (5*0.66)/4 ≈ 0.827

Od tu moramo.79 °

Končno je uporaba vsote notranjega kota trikotnika 180 °.8 °.