Tidecágono

Slika 1.- Na levi redni Tridecácágone in na desni valuti 20 kron Češke, s konturo v obliki Bridecagona, vpisane v obod, na eni strani ima lev Bohemije, na drugi pa San Wenceslao, Patron Češke republike, nameščene na konju. Vir: f. Zapata.

Kaj je Tridecágono?

TrideCagon je ravno geometrijska figura družine poligonov, za katero je značilno 13 strani in 13 točk. Drugo ime za ta poligon je Triskaidecágono, Številka, ki izhaja iz grščine.

13 strani so linijski segmenti, ki končno blizu oblikovanja slike. Poligoni, ki so poimenovani glede na količino strani, so bogat vir navdiha za arhitekturo, gradnjo in oblikovanje številnih predmetov, tako umetnost kot utilitarice.

Lastnosti Tridecágona

Tridecágono z drugimi poligoni deli naslednje značilnosti in lastnosti:

-Strani, So linijski segmenti, ki so združeni za oblikovanje figure, ki je v primeru Tridecágono 13. Identificirajo jih z malimi črkami.

-Točke, Tako se imenujejo križišča zaporednih strani in običajno označujeta z velikimi črkami. Tridecágono ima 13 vrst.

-Obseg, enakovredno vsoti strani. Če imajo vse strani enake mere "A", je obod preprosto 13 × A, če pa so stranice neenake, potem obod dodaja vsako dolžino strani.

-Center, To je točka, ki ohranja enako razdaljo tako z vrhovi kot na straneh.

-Diagonala, Linija, ki se pridruži točki drugemu, ki ni mogoče oceniti (zaporedne točke so združene s strani).

-Notranji koti, Nastaneta sta med dvema sosednjima stranicama figure in na notranjem delu poligona, njegova vrhova pa je skupna točka obeh strani.

Vam lahko služi: Miletus tak teorem

-Zunanji koti, So zunaj poligona, med eno stranjo in podaljšanje ene od zaporednih strani do prve.

-Radio, Razdalja razdalja-Vrtix Tridecágona.

-Osrednji kot, To je tisti, katerega točka je središče poligona.

-Apotem, segment, ki se pridruži sredini ene strani s sredino slike in tvori 90 ° s to stranjo.

Redni in nepravilen gromo

Threecaroni so lahko:

-Redno, Ko je mera vseh trinajstih strani enaka in njeni notranji koti merijo enako.

-Nepravilno, Če ima ena ali več strani različne ukrepe.

V primeru rednih Tridecácágone lahko uporabimo naslednje formule:

Notranji kot

Za navaden poligon je formula, ki omogoča izračun vrednosti notranjega kota,:

Kjer n predstavlja število strani, kar je v tem primeru 13. S to vrednostjo je:

I = (11 × 180 °)/13 ≈ 152.3. mesto

Diagonale

Število diagonalov se izračuna po naslednji formuli, celo veljavno, če je poligon nepravilen:

Za n = 13 rezultatov:

D = 13 × 10/2 = 65 diagonalov

Apotem

Vrednost apotema l_Do  Izračuna se z naslednjo formulo, ki je "A" dolžina strani:

L_Do ≅ 2.0286a

Območje

Če je obod p in dolžina apotema l_Do, Območje Tridecágono se izračuna z:

A = (p × l_Do)/2

Formula ostaja odvisno od strani "A":

A = (13a × l_Do)/2

Zamenjava ukrepa_Do Iz prejšnjega razdelka dobimo formulo za območje, ki je odvisna le od dolžine strani:

A = (13a × 2.0286a)/2 ≈ 13.186a²

Vam lahko služi: hipergeometrična porazdelitev: formule, enačbe, model

Vaja

Če je premer 20 mm krone 26 mm, koliko sta stranski in območje Tridecágono registrirano v krogu valute?

Rešitev

Iz slike je pravokotnik trikotnik, katerega kategorije so apotem in polovica dolžine strani, s hipotenusom, ki je enaka polmeru valute, ki je polovica premera. Ker je to vredno 26 mm, je radio r enak 13 mm.

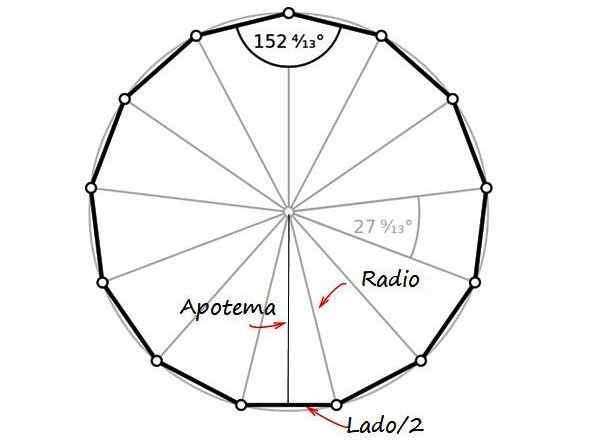Slika 2. Radio, apotema in polovica strani Trindecagona tvorijo pravokotnik trikotnik. Vir: Wikimedia Commons/F. Zapata.

Avtor pitagora teorem:

Ker l_Do ≈ 2.0286a, imate:

R² = (2.0286A)² + (0.5² = 4.3652a²

Stran je:

S to vrednostjo je območje valute:

A ≈ 13.186a² = 13.186 (6.222 mm)² = 510.5 mm²

Bralec je prepuščen primerjavi tega rezultata z območjem, pridobljenim s predpostavko, da je valuta okrožna polmera r = 13 mm.

Kako je Tridecágono?

Navadni Trindecagon je iz poligonov, ki ne priznavajo natančne konstrukcije samo s pravilom in kompasom, torej ni gradilni poligon. Vzpostavljajo jih le, vsaj teoretično, tisti poligoni, katerih število strani vključuje samo glavne dejavnike oblike:

Tako se imenujejo glavne številke Fermat Cousins, Toda številka 13, čeprav je bratranec, nima te oblike.

Vendar lahko narišete navaden Trindecagon, ki je registriran v obodu, vsaka točka ima križišče z njim, ne da bi ga opazili v golem očesu. Za to je potrebno.

Vam lahko služi: obtusagle Trikotnik

Eden od načinov za izgradnjo običajnega Tridecácágone, čeprav ne edini, je risanje potez, kot je prikazano v naslednji animaciji:

Slika 3. Gradnja običajnega tridecagona. Vir: Wikimedia Commons.

In ta druga animacija opisuje tudi, kako narediti približno Tridecágono približno, s pravilom in kompasom:

Slika 4.- Alternativni način za izgradnjo približno rednega tridecagona s pravilom in kompasom. Vir: Wikimedia Commons.

Primeri Tridecágela

Konkaven in konveksni grom

Ko so notranji koti Tridecágono manjši od 180 °, je številka konveksna, če je eden ali več notranjih kotov večji od 180 °, potem je Tridecágono konkavni.

Redni Tridecácágon je izbočen, saj njegovi notranji koti merijo približno 152.3. vsak.

Uporaba Tridecágono v numizmatiki

Češka krona

Numizmatika je znanost kovancev, medalj, vstopnic in čipov. Poligoni na številnih straneh so idealni kot dekorativni elementi pri oblikovanju kovancev, zlasti tistih, ki imajo številne strani, na primer Tridecágono.

Niso vsi kovanci okrogli, vendar poligoni na številnih straneh spominjajo na krožno obliko, več strani, večji je pristop. Zato oblikovalci kovancev na številnih straneh uporabljajo poligone, da v svoj dizajn uvedejo pridih izvirnosti.

S tem namenom se uporabljajo različni poligoni, kot je zgornja valuta, imenovana krona in iz Češke.

Reference

1. Aleksander, d. 2013. Geometrija. 5. Izdaja. Cengage učenje.
2. Risba. Redni poligoni. Okrevano od: risba.com.
3. Hartley, m. Konstruiranje tridecagona. Obnovil od: YouTube.com
4. Wikipedija. Gradbeni poligon. Okrevano od: je.Wikipedija.org.
5. Wikiwand. Tidecagon. Okreval od: wikiwand.com.