Lastnosti, razmerja in formule pravokotnika, primeri

A Pravokotnik trapez Gre za ravno štiri strani, tako da sta dva vzporedna med seboj, imenovana baze In tudi ena od drugih strani je pravokotna na podlagi.

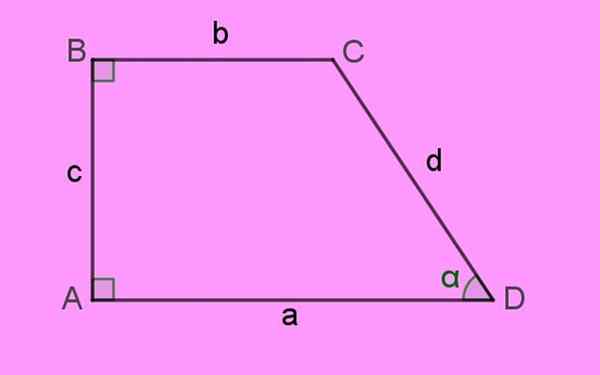
Zaradi tega sta dva notranja kota ravna, torej merita 90 °. Od tod tudi ime "pravokotnika", ki je dana figuri. Naslednja slika pravokotnika trapeze pojasnjuje te značilnosti:

[TOC]

Elementi trapeza

Elementi trapeza so:

-Baze

-Točke

-Višina

-Notranji koti

-Povprečna baza

-Diagonale

Te elemente bomo podrobno opredelili s pomočjo slik 1 in 2:

Slika 1. Trapez pravokotnika, za katerega je značilno dva notranja kota 90 °: A in B. Vir: f. Zapata.

Strani pravokotni trapezoida so označene z malimi črkami A, B, C in D. Vogali figure oz Točke Navedeni so z velikimi črkami. Končno Notranji koti Izraženi so z grškimi črkami.

Po definiciji baze Teh trapezoidov sta strani A in B, ki sta opažena vzporedna in imajo tudi različne dolžine.

Pravokotna stran do obeh podstavkov je stran c na levi strani, ki je višina h trapeza. In končno je stran D, ki tvori akutni kot α s stranjo a.

Vsota Notranji koti četrtletja je 360 ​​°. Zlahka cenimo, da je manjkajoči kot C na sliki 180 - α.

The povprečna baza To je segment, ki se pridružuje sredine strani ne -Paralelnih strani (segment EF na sliki 2).

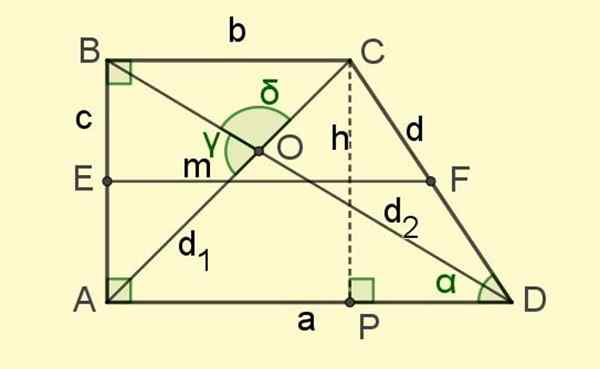Slika 2. Elementi pravokotnika trapeza. Vir: f. Zapata.

In končno obstajajo diagonale D₁ in d₂, Segmenti, ki združujejo nasprotne točke in se sekajo v točki O (glej sliko 2).

Odnosi in formule

Višina H trapeza

H = c

Obod str

To je merilo konture in se izračuna z dodajanjem strani:

Perimeter = a + b + c + d

Stran d Je izražen v višini ali strani c Skozi teorem pitagore:

D = √ (a-b)² + c²

Zamenjava v obodu:

P = a + b + c + √ (a-b)² + c²

Povprečna baza

To so poldele baz:

Srednja baza = (a+b)/2

Včasih najdemo povprečno bazo, izraženo na ta način:

Srednja baza = (glavna baza + manjša baza) /2

Območje

Območje A trapeza je produkt povprečne osnove po višini:

A = (Glavna baza + manjša baza) x višina /2

A = (a+b) c/2

Diagonale, strani in koti

Na sliki 2 se pojavlja več trikotnikov, tako pravokotniki kot tudi ne -preresniki. Tistim, ki imajo prav trikotnike, jih lahko uporabijo teorem pitagore in tisti, ki tega ne storijo, teoreme kosinusa in dojke.

Vam lahko služi: transcendentne številke: kaj so, formule, primeri, vaje

Na ta način obstajajo odnosi med stranicami in med stranicami in notranjimi koti trapezio.

Trikotnik CPA

To je pravokotnik, noge so enake in so vredne B, hipotenuza pa je diagonala D₁, Zato:

d₁² = b² + b² = 2b²

Dab trikotnik

Je tudi pravokotnik, noge so do in c (ali tudi do in h) In hipotenuza je d₂, tako da:

d₂² = a² + c² = a² + h²

Trikotnik CDA

Ker ta trikotnik ni pravokotnik, se nanese kosinus.

Glede na teorem Coseno:

d₁² = a² + d² - 2ad cos α

Trikotnik CDP

Ta trikotnik je pravokotnik in s svojimi stranicami so zgrajeni trigonometrični razlogi kot α:

sin α = h/d

cos α = pd/d

Toda PD = A - B stran, torej:

cos α = (a -b) / d → a - b = d cos α

a = b + d cos α

Imate tudi:

TG α = sin α / cos α = H / (A-B) → H = TG α (A-B)

Trikotnik CDB

V tem trikotniku imamo kot, katerega vrha je v C. Na sliki ni označen, toda na začetku je izkazalo, da je vredno 180 - α. Ta trikotnik ni pravokotnik, zato je mogoče nanesti teorem za kosinus ali teorem dojk.

Zdaj je enostavno dokazati, da:

Sen (180 - α) = sin α

cos (180 - α) = - cos α

Uporaba teorema o Coseno:

d₂² = d² + b² - 2db cos (180 - α) = d² + b² + 2db cos α

Primeri pravokotnikov

Trapezi in zlasti pravokotniki najdemo na številnih straneh, včasih pa ne vedno oprijemljivi. Tu imamo več primerov:

Trapecio kot oblikovalski element

Geometrijske figure je veliko v arhitekturi številnih zgradb, kot je ta cerkev v New Yorku, ki prikazuje strukturo v obliki pravokotnika trapeza.

Tudi trapezalna oblika je pogosta pri načrtovanju zabojnikov, posod, rezil (Rezalnik ali natančno), listi in v grafičnem oblikovanju.

Slika 3. Angel znotraj pravokotnika trapezoida v cerkvi v New Yorku. Vir: David Goehring prek Flickr.

Generator trapeznega vala

Električni signali niso le kvadratni, sinus ali trikotni. Obstajajo tudi trapezoidni signali, ki so uporabni v številnih vezjih. Na sliki 4 je trapezoidni signal, sestavljen iz dveh pravokotnikov. Med njimi tvorijo en sam izoscele trapez.

Vam lahko služi: delitve 8: Kaj so in lahka razlaga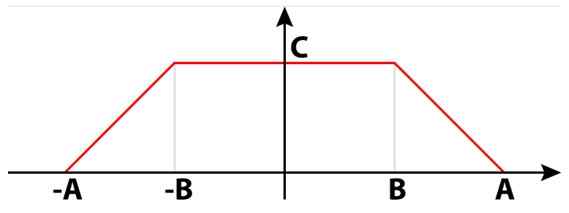Slika 4. Trapezoidni signal. Vir: Wikimedia Commons.

V numeričnem izračunu

Za numerično izračunavanje določenega integrala funkcije F (x) med A in B se pravilo trapeze uporablja za približevanje območja pod grafom F (x). Na naslednji sliki so na levi integralni pristopi z enim pravokotnim trapezoidom.

Boljši pristop je prave figure z več pravokotniki.

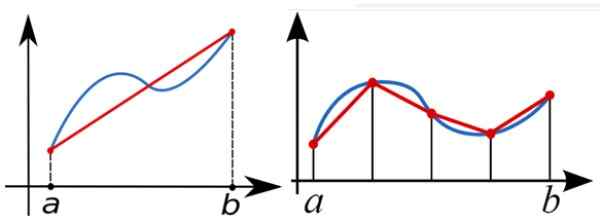Slika 5. Določen integral med A in B ni nič drugega kot območje pod krivuljo F (x) med temi vrednostmi. Pravokotnik trapezoid lahko služi kot prvi pristop k temu območju, toda več kot trapezoidi se uporabljajo, boljši je pristop. Vir: Wikimedia Commons.

Trapezoidni tovorni žarek

Sile niso vedno osredotočene na eno samo točko, saj imajo telesa, na katerih delujejo. Takšen je primer mostu, skozi katerega vozila neprestano krožijo, voda bazena na navpičnih stenah istega ali strehe, na kateri se nabira voda ali sneg.

Zato se sile porazdelijo na enoto dolžine, površine ali volumna, odvisno od telesa, od katerega delujejo.

V primeru snopa ima lahko sila, porazdeljena na enoto dolžine, različne porazdelitve, na primer pri pravokotniku Trapeze, prikazani spodaj:

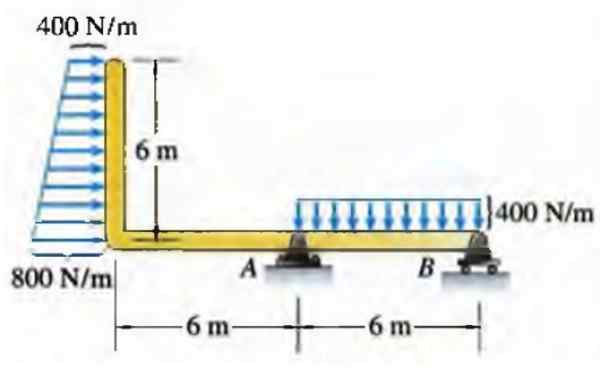Slika 6. Obremenitve na snopu. Vir: Bedford, do. Devetnajst devetdeset šest. Statična. Addison Wesley Interamerican.

V resnici ne vedno distribucije ustrezajo običajnim geometrijskim oblikam, kot je ta, vendar so lahko v mnogih primerih dober pristop.

Kot izobraževalno in učno orodje

Bloki in listi z geometrijskimi oblikami, vključno s trapezoidi, so zelo koristni za otroke, da se že od malih nog seznanijo z očarljivim svetom geometrije.

Slika 7. Bloki s preprostimi geometrijskimi oblikami. Koliko pravokotnikov je skritih v blokih? Vir: Wikimedia Commons.

Rešene vaje

- Vaja 1

V pravokotniku trapez na sliki 1 je največja podlaga vredna 50 cm, najmanjša podlaga pa je enaka 30 cm, znano je tudi, da poševna stran meri 35 cm. Najti:

a) kot α

b) višina

c) obod

d) Srednja baza

e) Območje

f) diagonala

Rešitev

Podatki o izjavi so povzeti na ta način:

A = višja osnova = 50 cm

B = manjša osnova = 30 cm

D = nagnjena stran = 35 cm

Vam lahko služi: osnovne operacije

Če želite najti kot α, obiščemo razdelek Formule in enačbe, da vidimo, kateri najbolje ustreza ponujenim podatkom. Iščeni kot najdemo v več analiziranih trikotnikih, na primer CDP.

Tam imamo to formulo, ki vsebuje neznano in tudi podatke, ki jih poznamo:

cos α = (a-b) / d

Zato:

α = loki [(a-b) / d] = loki [(50-30) / 35] = loki 20/35 = 55.15 °

Rešitev b

Iz enačbe:

sin α = h/d

H:

h = d.greh α = 35 Sen 55.15 ° cm = 28.72 cm

Rešitev c

Obod je vsota strani, in ker je višina enaka strani C, moramo:

C = H = 28.72 cm

Zato:

P = (50 + 30 + 35 + 28.72) cm = 143.72 cm

Rešitev d

Povprečna osnova so poldele baz:

Srednja osnova = (50 + 30 cm)/2 = 40 cm

Rešitev e

Trapezoidno območje je:

A = povprečna osnovna višina x = 40 cm x 28.72 = 1148.8 cm².

Rešitev f

Za diagonalno d₁ To formulo je mogoče uporabiti:

d₁² = b² + b² = 2b²

d₁²= 2 x (30 cm)² = 1800 cm²

d₁ = √1800 cm² = 42.42 cm

In za diagonalno d₂:

d₂² = d² + b² + 2db cos α = (35 cm)² + (30 cm)² + 2 x 35 x 30 cm² Cos 55.15 ° = 3325 cm²

d₂ = √ 3325 cm² = 57.66 cm

To ni edini način za iskanje D₂, Ker obstaja tudi dab trikotnik.

- Vaja 2

Naslednji graf hitrosti, odvisno od mobilnega telefona, ki ima enakomerno pospešeno pravokotno gibanje. Izračunajte razdaljo, ki jo mobilni telefon prevozi v časovnem intervalu med 0.5 in 1.2 sekundi.

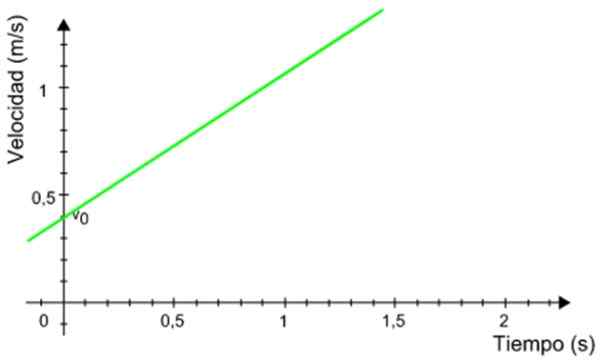Slika 8. Grafična proti času mobilnega telefona z enakomerno pospešenim gibanjem Reknet. Vir: Wikimedia Commons.

Rešitev

Razdalja, ki jo prevozi mobilni telefon, je enakovredna območju pod grafiko.

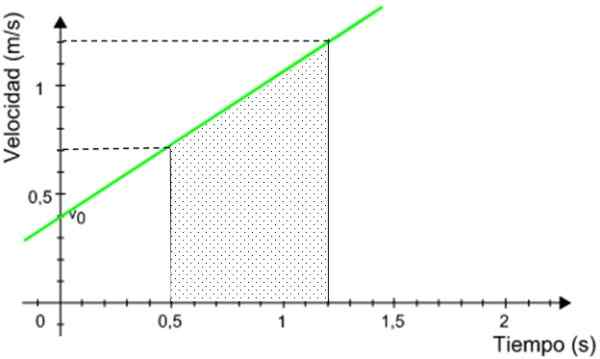Slika 9. Razdalja, ki jo prevozi mobilni telefon, je enakovredna območju pod grafiko. Vir: Spremenjeno s F. Zapata.

Zasenčeno območje je območje pravokotnika trapezoida, ki ga daje:

A = (Glavna baza + manjša baza) x višina /2

A = (1.2 + 0.7) m/s x (1.dvajset.5) s/2 = 0.665 m

Reference

1. Baldor, a. 2004. Ravna in vesoljska geometrija s trigonometrijo. Kulturne publikacije.
2. Bedford, a. Devetnajst devetdeset šest. Statična. Addison Wesley Interamerican.
3. Jr. Geometrija. 2014. Poligoni. Lulu Press, Inc.
4. OnlinemsChool. Pravokotnik trapez. Okrevano od: je.OnlinemsChool.com.
5. Samodejno reševanje problemov z geometrijo. Trapez. Okrevano od: Scuolaetrica.Predmet
6. Wikipedija. Trapecio (geometrija). Okrevano od: je.Wikipedija.org.