Lastnosti, odnosi in formule Trapecio Isosceles, primeri

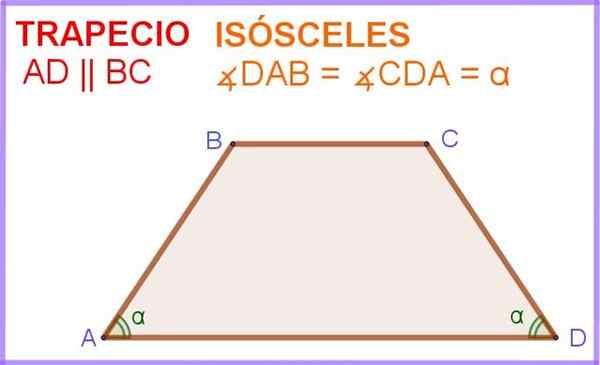
A trapez izosceles To je štirikolesnik, v katerem sta dve strani vzporedni med seboj in tudi dva kota, ki mejita na eno od teh vzporednih strani.

Na sliki 1 imate kvadrilateralno ABCD, v katerem sta stranski AD in BC vzporedni. Poleg tega imata kota ∠dab in ∠adc, ki mejijo na vzporedni stranski oglas. 

Slika 1. Trapezijevi izosceles. Vir: f. Zapata.

Tako je ta kvadrilateralen ali štiristranski poligon dejansko izoscelijski trapez.

V trapezu se imenujejo vzporedne strani baze in neresnične se imenujejo bočna. Druga pomembna značilnost je višina, ki je razdalja, ki ločuje vzporedne strani.

Poleg isosceles trapezoida obstajajo tudi druge vrste trapeza:

-TRapecio Escaleno, ki ima vse svoje različne kote in stranice.

-TPravokotnik rapecio, v katerem ima stran ravne sosednje kote.

Trapezalna oblika je pogosta na različnih področjih oblikovanja, arhitekture, elektronike, izračuna in še veliko več, kot bomo videli kasneje. Od tod pomembnost, da se seznanijo s svojimi lastnostmi.

[TOC]

Lastnosti

Ekskluzivni izosceles trapez

Če je trapez izosceles, potem izpolni naslednje značilne lastnosti:

1.- Strani imajo isti ukrep.

2.- Koti, ki mejijo na baze, so enaki.

3.- Nasprotni koti so dopolnilni.

4.- Diagonale imajo enako dolžino, enaka sta dva segmenta, ki združujeta nasprotne točke.

5.- Kot, ki nastane med osnovami in diagonali, je enak ukrep.

6.- Omejenega obsega je.

Vzajemno, če se trapez sreča s katero koli od prejšnjih lastnosti, potem je to izoscelijski trapez.

Če je v trapezu izosceles eden od kotov ravno (90 °), potem bodo tudi vsi drugi koti, ki tvorijo pravokotnik. To pomeni, da je pravokotnik poseben primer isosceles trapezoida.

Slika 2. Zabojniki za koruzne palomite in šolske mize so oblikovane kot izoscele. Vir: pxfuel (levo)/McDowell Craig skozi Flickr. (prav)

Za vse trapez

Naslednji niz lastnosti velja za vsak trapez:

7.- The mediana Trapeza je to segment, ki se pridruži središča njenih neparalnih strani, vzporedno s katero koli bazo.

8.- Dolžina mediana je enaka polsemumu (vsota, deljena z 2) dolžine njegovih baz.

9.- Mediana trapeza reže svoje diagonale na sredini.

10.- Diagonale trapeza se sekajo na točki, ki jih razdeli na dva odseka, sorazmerno s količniki baz.

enajst.- Vsota kvadratov diagonale trapeza je enaka vsoti kvadratov stranskih strani in dvojnega izdelka njegovih baz.

Lahko vam služi: koliko tisoč se prilega v desetino?

12.- Segment, ki se pridruži srednjim diagonalnim točkam.

13.- Koti, ki mejijo na strani, so dopolnilni.

14.- Trapez ima registriran obseg, če in samo, če je vsota njegovih baz enaka vsoti njegovih strani.

petnajst.- Če ima trapez registriran obseg, potem so koti z vrhom v središču omenjenega oboda in strani, ki potekajo skozi konce iste strani, ravni koti.

Odnosi in formule

Naslednji niz odnosov in formul se nanaša na sliko 3, kjer poleg izosceles trapezoida že omenjene druge pomembne segmente, kot so diagonale, višina in medij.

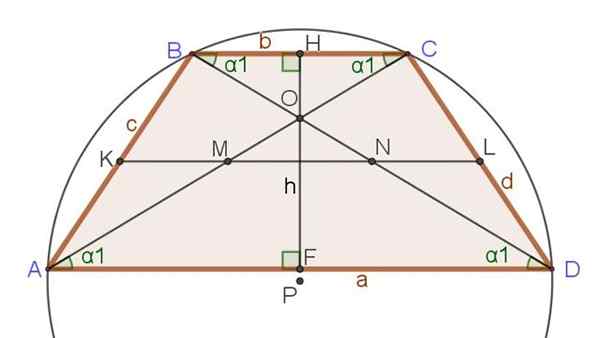Slika 3. Mediana, diagonale, višina in obod, prepisani v trapezu izosceles. Vir: f. Zapata.

Ekskluzivni odnosi Isosceles Trapecio

1.- Ab = dc = c = d

2.- ∡dab = ∡cda in ∡abc = ∡bcd

3.- ∡dab + ∡bcd = 180 ° in ∡cda + ∡abc = 180 °

4.- Bd = ac

5.- ∡CAD = ∡BDA = ∡cbd = ∡BCA = α₁

6.- A, B, C in D spadajo v opisan obod.

Odnosi za kateri koli trapez

7. Če je Ak = kb in dl = lc ⇒ kl || Oglas in kl || Pr

8.- Kl = (ad + bc)/2

9.- Am = mc = ac/2 in dn = nb = db/2

10.- Ao/oc = ad/bc y do/ob = ad/bc

enajst.- AC² + Db² = Ab² + DC² + 2⋅ADVBC

12.- Mn = (oglas - BC)/2

13.- ∡dab + ∡abc = 180 ° in ∡cda + ∡bcd = 180 °

14.- Če je AD + BC = AB + DC ⇒ ∃ R, kaj Equidista AD, BC, AB in DC

petnajst.- Če ∃ r, kaj enakosta AD, BC, AB in DC, potem:

∡bra = ∡drc = 90 °

Trapezoidni odnosi izosceles z registriranim obodom

Če je v izosceles trapezoidu vsota baz je enaka dvojni strani, potem je tu registrirani obod.

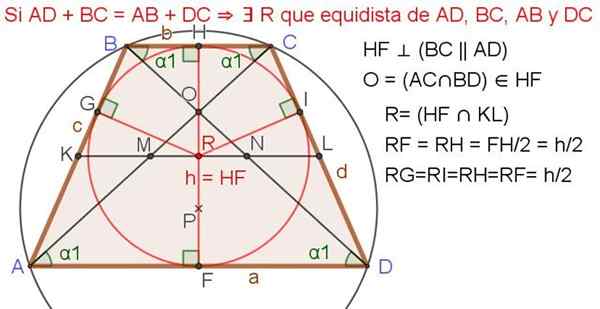Slika 4. Trapez z registriranim obodom. Vir: f. Zapata.

Naslednje lastnosti veljajo, ko ima trapezoid izosceles registriran obseg (glej sliko 4 zgoraj):

16.- Kl = ab = dc = (ad + bc)/2

17.- Diagonale so razrezane pod pravim kotom: AC ⊥ BD

18.- Višina je enaka srednji: hf = kl, to je h = m.

19.- Kvadrat višine je enak produktu baz: H² = Bc⋅AD

dvajset.- V teh specifičnih pogojih je območje trapeza enako kvadratu višine ali produktu baz: območje = H² = Bc⋅AD.

Formule za določitev ene strani, znane druge in kot

Znana ena osnova, stran in kot, drugo osnovo je mogoče določiti z:

a = b + 2c cos α

B = a - 2c cos α

Če je dolžina baz znana kot znana in kot, je dolžina obeh strani:

Lahko vam služi: fermat mejo: kaj je sestavljeno in rešene vaje

C = (a - b) / (2 cos α)

Določitev na eni strani, znana ostala in diagonala

A = (D₁² - c²)/ B;

B = (D₁² - c²)/ do 

C = √ (d₁² - A⋅B)

Kjer d₁ To je dolžina diagonalov.

Osnova od višine, območja in druge baze

a = (2 a)/h - b

b = (2 a)/h - a

Znane nazaj v bazah, območju in kotu

C = (2a) /[(a + b) sin α]

Znana bočna mediana, območje in kot

C = a / (m.greh α)

Znana višina strani

H = √ [4 c² - (A - B)²]

Znana višina kot in dve strani

H = tg α⋅ (a - b)/2 = c . greh α

Znane diagonale vse strani ali dve strani in kot

d₁ = √ (c²+ a b)

d₁ = √ (a²+ c² - 2 a c cos α)

d₁ = √ (b² + c²- 2 B C cos β)

Isosceles trikotnik obod 

P = a + b + 2c

Trapezoidno območje izosceles

Za izračun območja je več formul, odvisno od znanih podatkov. Naslednje je najbolj znano, odvisno od baz in višine:

A = h⋅ (a + b)/2

In te druge je mogoče uporabiti tudi:

-Če so znane strani

A = [(a +b)/4] √ [4c² - (A - B)²]

-Ko imate dve strani in kot

A = (b + c cos α) c sena α = (a - c cos α) c sena α

-Če je polmer registriranega oboda znan in je kot

A = 4 r² / Sin α = 4 r² / Greh β

-Ko so znane baze in kot

A = A⋅B / SIN α = A⋅B / SEN β 

-Če je trapez mogoče registrirati obseg

A = C⋅√ (A⋅B) = m⋅√ (a⋅B) = r⋅ (a + b)/2

-Poznali diagonale in kot, ki se tvorijo med seboj

A = (D₁²/2) sen γ = (d₁² / 2) Sen δ 

-Ko imate stran, mediano in kot

A = mc.greh α = mc.Sen β

Obkrožen obodni radio

Samo izosceles trapezoidi imajo omejen obseg. Če je znana glavna podlaga, stran c in diagonala d₁, Potem je polmer r oboda, ki gre skozi štiri točke trapeza,:

R = a⋅c⋅d₁ / 4√ [p (p -a) (p -c) (p -d₁)

Kjer je p = (a + c + d₁) / 2

Primeri uporabe izosceles trapezoida

Trapezoid izosceles se pojavlja na področju oblikovanja, kot je prikazano na sliki 2. In tukaj imamo nekaj dodatnih primerov:

V arhitekturi in gradnji

Starodavni Inkas je poznal trapezoid izoscele in ga uporabljal kot gradbeni element v tem oknu Cuzco, Peru:

Slika 5 . Okno s trapezoidno obliko Coricancha, Cuzco. Vir: Wikimedia Commons.

In tu se v klicu spet pojavi trapezoid Trapezoidni list, Pogosto uporabljen material v konstrukciji:

Slika 6. Trapezna kovinska plošča začasno ščiti okna stavbe. Vir: Wikimedia Commons.

V oblikovanju

Že smo videli, da se isosceles trapezoid pojavlja v vsakdanjih predmetih, vključujoča hrana, kot je ta čokoladna bar:

Slika 7. Čokoladna palica, katere obrazi so oblikovani kot izoscele. Vir: Pxfuel.

Rešene vaje

- Vaja 1

Trapezoid izosceles temelji na 9 cm, osnova manj kot 3 cm in njene diagonale po 8 cm. Izračunati:

Lahko vam služi: splošna enačba parabole (primeri in vaje)

a) stran

b) višina

c) obod

d) ärea

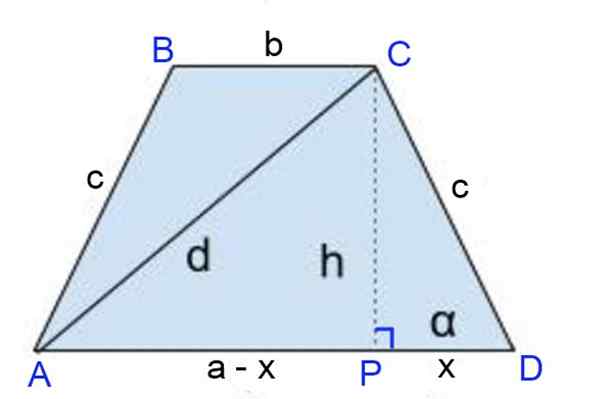Slika 8. Shema za vajo 1. Vir: f. Zapata

Rešitev

Višina CP = H je narisana, kjer vzhod višine definira segmente:

Pd = x = (a-b)/2 in 

Ap = a - x = a - a/2 + b/2 = (a + b)/2.

Skozi teorem pitagore do trikotnika pravokotnika DPC:

c² = h² + (A - B)² /4

In tudi do trikotnika pravokotnika APC:

d² = h² + Ap² = h² + (A+B)² /4

Končno se odšteje član, druga enačba prvega in poenostavi:

d² - c² = ¼ [(a+b)² - (A-B)²] = ¼ [(a+b+a-b) (a+b-a+b)]

d² - c² = ¼ [2a 2b] = a b

c²= d² - A b ⇒ c = √ (d² - a b) = √ (8² - 9⋅3) = √37 = 6,08 cm

Rešitev b

h² = d² - (A+B)² /4 = 8² - (12² / 2² ) = 8² - 6² = 28

H = 2 √7 = 5,29 cm

Rešitev c

Perimeter = A + B + 2 C = 9 + 3 + 2⋅6,083 = 24.166 cm

Rešitev d

Območje = H (A+B)/2 = 5,29 (12)/2 = 31,74 cm

- Vaja 2

Obstaja trapez izosceles, katerega največja osnova je dvakrat manjša, njegova najmanjša podlaga pa je enaka višini, ki je 6 cm. Določiti:

a) strani strani

b) obod

c) Območje

d) koti

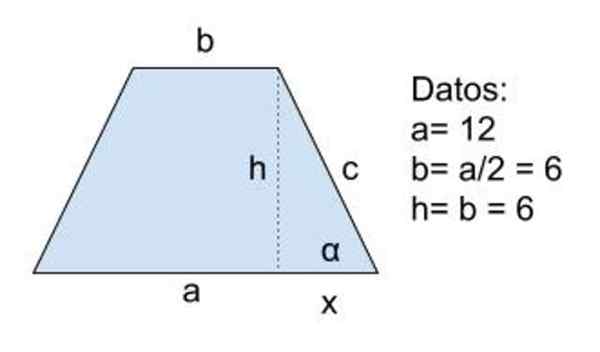Slika 8. Shema za vajo 2. Vir: f. Zapata

Rešitev

Podatki: a = 12, b = a/2 = 6 in h = b = 6

Nadaljujemo na ta način: višina H je narisana in teorem pitagore se uporablja za trikotnik hipotenuze "C" in Catetos H in X:

c² = h²+Xc²

Nato morate izračunati vrednost višine iz podatkov (H = B) in Cateto X: 

a = b + 2 x ⇒ x = (a-b)/2

Zamenjava prejšnjih izrazov imate:

c² = b²+(A-B)²/2²

Zdaj so uvedene in poenostavljene številčne vrednosti:

c² = 62+ (12-6) 2/4

c² = 62 (1+¼) = 62 (5/4)

Pridobivanje:

C = 3√5 = 6,71 cm

Rešitev b

Obod p = a + b + 2 c

P = 12 + 6 + 6√5 = 6 (8 + √5) = 61,42 cm

Rešitev c

Območje, ki temelji na višini in dolžini baz, je:

A = H⋅ (A + B)/2 = 6⋅ (12 + 6)/2 = 54 cm²

Rešitev d

Kot α, ki tvori stran z glavno osnovo, dobimo s trigonometrijo:

Tan (α) = h / x = 6/3 = 2

α = arctan (2) = 63,44 °

Drugi kot, ki tvori stran z manjšo osnovo, je β, ki je dopolnil α:

β = 180 ° - α = 180 ° - 63,44 ° = 116,56 °

Reference

1. In. Do. 2003. Elementi geometrije: z vajami in geometrijo kompasa. Univerza v Medellinu.
2. Campos, f. 2014. Matematika 2. Uredniška skupina Patria.
3. Osvobojen, k. 2007. Odkrijte poligone. Benchmark Education Company.
4. Hendrik, v. 2013. Splošni poligoni. Birkhäuser.
5. Iger. Matematika Prvi semester Tacaná. Iger.
6. Jr. Geometrija. 2014. Poligoni. Lulu Press, Inc.
7. Miller, Heeren in Hornsby. 2006. Matematika: sklepanje in aplikacije. 10.  Izdaja. Pearson Education.
8. Patiño, m. 2006. Matematika 5. Uredništvo Progreso.
9. Wikipedija. Trapez. Okrevano od: je.Wikipedija.com