Lastnosti, formule in enačbe Escaleno trapezio, primeri

A trapez Scalene Gre za štirikolesni poligon, od katerih sta dva vzporedna med seboj in s štirimi notranjimi koti različnih ukrepov.

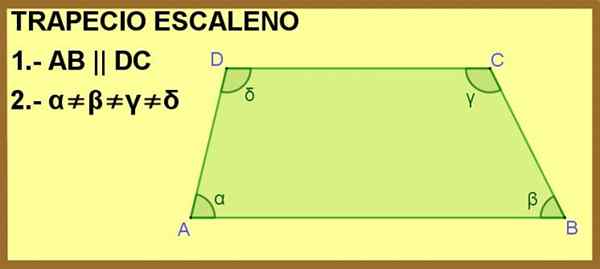
Prikazan je kvadrilateralen ABCD, kjer sta strani AB in DC vzporedni med seboj. S tem je dovolj, da postane trapez, poleg tega pa so notranje kote α, β, γ in δ različni, zato je trapezoid Escalano.

Slika 1. Quadrilateralni ABCD je trapez za stanje 1 in Scalene za stanje 2. Vir: f. Zapata.

[TOC]

Elementi Scaleno Trapact

Pod najbolj značilnimi elementi:

-Baze in stran: Vzporedne strani trapezoida so njegove podlage in dve neparalni strani sta strani.

V trapeziju Scale so baze različnih dolžin in strani tudi. Vendar ima lahko trapezoid Scalena stran enake dolžine kot podlaga.

-Mediana: Segment se pridruži sredinskim točkam strani.

-Diagonala: Diagonala trapeza je segment, ki se pridruži dve nasprotni točki. Trapez, tako kot vsak štirikotnik, ima dve diagonali. V trapezio Scale so različne dolžine.

Drugi trapezoidi

Poleg Escaleno Trapezio obstajajo tudi drugi posebni trapezoidi: pravokotnik trapezoid in izosceles trapezoid.

Trapez je pravokotnik, ko je eden od njegovih kotov ravno, medtem ko ima trapezio izoscele svoje stranice enake dolžine.

Trapezalna oblika ima številne aplikacije na ravni oblikovanja in industrije, na primer v konfiguraciji kril letala, oblika vsakodnevnih predmetov, kot so mize, varnostne kopije stolov, posode, denarnice, tekstilni odtisi in še več.

Slika 2. Trapezna oblika je pogosta v konfiguraciji zrakoplovov Alar. Vir: Wikimedia Commons.

Lastnosti

Nato so naštete lastnosti plezalnega trapeza, od katerih so številne obsežne za druge vrste trapezoida. V nadaljevanju, ko govorite o "Trapezio", bo lastnost uporabna za kakršne koli vrste, vključno s Scalene.

1. Mediana trapezoida, torej segment, ki združuje srednje točke njegovih neparalnih strani, je vzporeden s katero koli bazo.

2.- Mediana trapezoida ima dolžino, ki je pol -som njegovih baz in na sredini reže svoje diagonale.

3.- Diagonale trapeza se sekajo na točki, ki jih razdeli na dva odseka, ki sta sorazmerna z razmerjem baz.

4.- Vsota kvadratov diagonale trapeza je enaka vsoti kvadratov stranskih strani in dvojnega izdelka njegovih baz.

5.- Segment, ki se pridruži srednjim diagonalnim točkam.

Vam lahko služi: injektivna funkcija: iz česa je sestavljena, kaj je in primeri

6.- Koti, ki mejijo na strani, so dopolnilni.

7.- V trapezi Scale je dolžina njegovih diagonalov drugačna.

8.- Trapez ima registriran obseg le, če je vsota njegovih baz enaka vsoti njegovih strani.

9.- Če ima trapez registriran obseg, potem je kot z vrhom v središču omenjenega oboda in stranice, ki prehajajo skozi konce stranske trapeze, naravnost.

10.- Trapez Escaleno nima omejenega obsega, edina vrsta trapeze.

Formule in enačbe

Naslednji odnosi plezalnega trapeza se nanašajo na naslednjo sliko.

1.- Če ae = ed in bf = fc → ef || AB in EF || DC.

2.- EF = (AB + DC)/2, to je: M = (A + C)/2.

3.- Di = ib = d₁ /2 in ag = gc = d₂ /2.

4.- Dj / jb = (c / a) podobno cj / ja = (c / a).

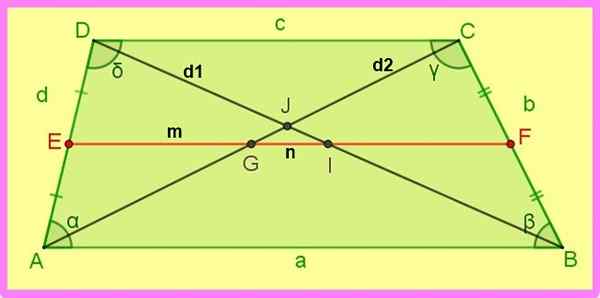Slika 3. Mediana in diagonale trapezoida skale. Vir: f. Zapata.

5.- Db² + AC² = Oglas² + Pr² + 2 AB ∙ DC 

Enako:

d₁² + d₂² = d² + b² + 2 a ∙ c

6.- Gi = (ab - dc)/2

To pomeni:

n = (a - c)/2

7.- α + Δ = 180⁰ in β + γ = 180⁰

8.- Če α ≠ β ≠ γ γ Δ, potem d1 ≠ d2.

9.- Slika 4 prikazuje skalni trapez, ki ima registriran obseg, v tem primeru je izpolnjeno:

A + C = D + B

10.- V trapezu ABCD Escalene z registriranim centrom centra ali pa je izpolnjeno tudi naslednje:

∡aod = ∡boc = 90⁰

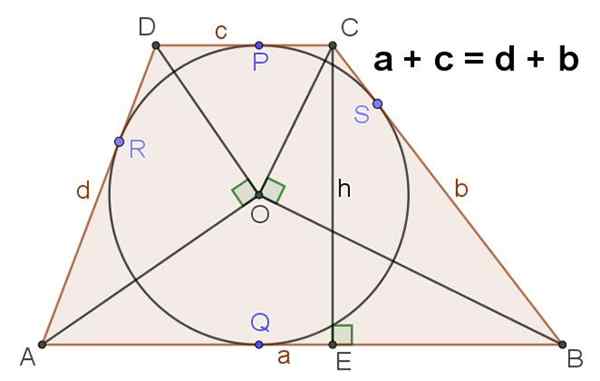Slika 4. Če je v trapezu preverjeno, da je vsota njegovih baz enaka vsoti strani. Vir: f. Zapata.

Višina

Višina trapeza je opredeljena kot segment, ki sega od točke osnove pravokotno do nasprotne osnove (ali njenega podaljška).

Vse višine trapeza imajo enak ukrep h, zato se večino časa višina besede nanaša na njegovo meritev. Skratka, višina je razdalja ali ločitev med bazami.

Višina H je mogoče določiti, če je znana dolžina strani in enega od kotov, ki mejijo na stran:

H = D sin (α) = D sin (γ) = b sin (β) = b sin (δ)

Mediana

M Mediana mera trapezoida so poldele baz:

M = (a + b)/2

Diagonale

d₁ = √ [a² + d² - 2 ∙ a ∙ d ∙ cos (α)]

d₂= √ [a² + b² - 2 ∙ a ∙ b ∙ cos (β)]

Izračunamo ga lahko tudi, če je znana le dolžina trapezoida:

d₁ = √ [b² + A ∙ c - a (b² - d²)/(a - c)]

d₂ = √ [d² + A ∙ c - a (d² - b²)/(a - c)]

Obseg

Obod je skupna dolžina konture, torej vsota vseh njegovih strani:

Vam lahko služi: diskretna naključna spremenljivka

P = a + b + c + d

Območje

Področje trapeza je poldele njegovih baz, pomnoženih z njegovo višino:

A = h ∙ (a + b)/2

Izračunamo ga lahko tudi, če sta znana srednja M in višina:

A = m ∙ h

V primeru, da je znana le dolžina trapezoidnih strani, lahko območje določimo s Herónovo formulo za trapezoid:

A = [(A+C)/| A-C |] ∙ √ [(S-A) (S-C) (S-A-D) (S-A-B)]]

Kjer je S polperimeter: s = (a+b+c+d)/2.

Drugi odnosi za plezanje

Rez mediane z diagonali in vzporednico, ki gre skozi presečišče diagonalov, povzroči druge odnose.

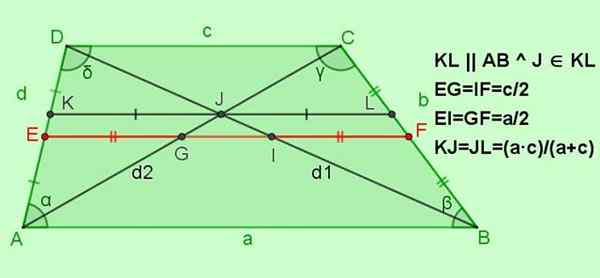Slika 5. Drugi odnosi za plezanje. Vir: f. Zapata.

-Odnosi za mediano EF

Ef = (a+c)/2; Npr = if = c/2; Ei = gf = a/2

-Odnosi za vzporedni segment do baz KL in to prehaja skozi točko Križišče j diagonale

DA KL || Ab || DC z j ∈ Kl, potem kj = jl = (a ∙ c)/(a+c)

Konstrukcija trapezija Scalene s pravilom in kompasom

Glede na podlage dolžin do in c, biti a> c in s strani dolžin b in d, biti b> d, Nadaljujemo po teh korakih (glej sliko 6):

1.- S pravilom je narisan segment največjega AB.

2.- Iz SE in na AB je točka P označena tako, da je AP = C.

3.- S kompasom s C in Radio D Center se nariše lok.

4.- Je v središču B z radiom B risanje loka, ki razlaga lok, sestavljen v prejšnjem koraku. Kličemo, da točka križišča.

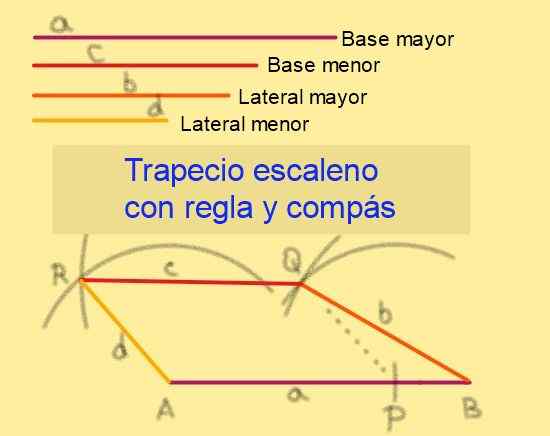Slika 6. Gradnja Escaleno Trapecio glede na svoje strani. Vir: f. Zapata.

5.- S središčem pri risanju polmera lok d.

6.- S središčem, v katerem lahko narišete lok polmera, ki je prestregel lok, sestavljen v prejšnjem koraku. Poklicali se bo na rezalno točko.

7.- Segmenti BQ, QR in RA so sestavljeni s pravilom.

8.- Quadrilateralni ABQR je skalni trapez, saj je APQR paralelogram, kar zagotavlja, da AB || Qr.

Primer

Naslednje dolžine so podane v cm: 7, 3, 4 in 6.

a) Ugotovite, ali lahko z njimi sestavite trapez skale, ki lahko omeji na obod.

b) Poiščite obod, območje, dolžino diagonalov in višino omenjene trapeze ter polmer registriranega oboda.

- Rešitev

Uporaba segmentov dolžine 7 in 3 kot bazah in dolžine 4 in 6 kot stranskih straneh je mogoče zgraditi trapezoid Scalene s postopkom, opisanim v prejšnjem razdelku.

Preveriti moramo, ali ima registriran obseg, vendar se spomnimo nepremičnine (9):

Vam lahko služi: šesterokotna prizma

Trapez ima registriran obseg le, če je vsota njegovih baz enaka vsoti njegovih strani.

To res vidimo:

7 + 3 = 4 + 6 = 10

Potem je izpolnjen pogoj vpisanega oboda.

- Rešitev b

Obseg

Obod P dobimo z dodajanjem strani. Ker se baze znašajo 10 in tudi strani, je obod:

P = 20 cm

Območje

Za določitev območja se uporablja le na njegovih straneh se uporablja razmerje:

A = [(A+C)/| A-C |] ∙ √ [(S-A) (S-C) (S-A-D) (S-A-B)]]

Kjer je S polperimeter:

S = (a+b+c+d)/2.

V našem primeru je polperimeter vreden s = 10 cm. Po zamenjavi ustreznih vrednosti:

A = 7 cm; b = 6 cm; C = 3 cm; D = 4 cm

Je ostalo:

= [10/4] √ [(3) (7) (-1) (-3)] = (5/2) √63 = 19,84 cm².

Višina

Višina H je povezana z območjem A do naslednjega izraza:

A = (a+c) ∙ h/2, kjer lahko višino dobimo z odmikom:

H = 2a / (a+c) = 2 * 19,84 / 10 = 3,968 cm.

Registriran obodni radio

Polmer registriranega oboda je vreden polovice višine:

R = h/2 = 1,984 cm

Diagonale

Končno obstaja dolžina diagonalov:

d₁ = √ [b² + A ∙ c - a (b² - d²)/(a - c)]

d₂ = √ [d² + A ∙ c - a (d² - b²)/(a - c)]

Pravilno nadomeščanje vrednosti je:

d₁ = √ [6² + 7 ∙ 3 - 7 (6² - 4²)/(7 - 3)] = √ (36+21-7 (20)/4) = √ (22)

d₂ = √ [4² + 7 ∙ 3 - 7 (4² - 6²)/(7-3)] = √ (16+21-7 (-20)/4) = √ (72)

To je: D₁ = 4,69 cm in d₂ = 8,49 cm

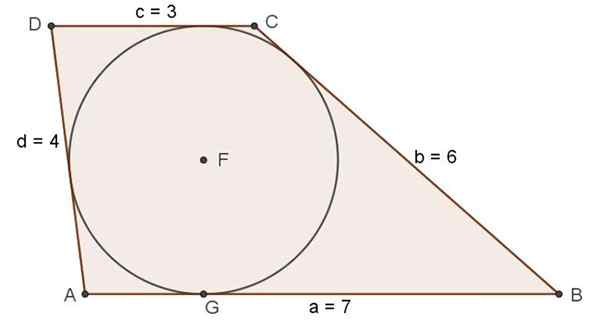Slika 7. Scalene trapezio, ki ustreza stanju obstoja registriranega oboda. Vir: f. Zapata.

Vaja rešena

Določite notranje kote osnovnega trapezoida AB = A = 7, CD = C = 3 in stranski Bc = B = 6, da = D = 4.

Rešitev

Za določitev kotov se lahko uporabi kosinusni teorem. Na primer, kot ∠a = α je določen iz trikotnika Abd z Ab = A = 7, Bd = D2 = 8,49 in DA = D = 4.

Teorem za kosinus, ki se nanaša na ta trikotnik, ostaja takšen:

d₂² = a² + d² - 2 ∙ a ∙ d ∙ cos (α), to je:

72 = 49+16-56 ∙ COS (α).

Pri čiščenju dobimo kosinus kota α:

Cos (α) = -1/8

To pomeni, da je α = arccos (-1/8) = 97.18⁰.

Na enak način dobimo druge kote, saj so njihove vrednote:

β = 41,41⁰; γ = 138,59⁰ in končno Δ = 82,82⁰.

Reference

1. C. In. Do. (2003). Elementi geometrije: z vajami in geometrijo kompasa. Univerza v Medellinu.
2. Campos, f., Cerecedo, f. J. (2014). Matematika 2. Uredniška skupina Patria.
3. Osvobojen, k. (2007). Odkrijte poligone. Benchmark Education Company.
4. Hendrik, v. (2013). Splošni poligoni. Birkhäuser.
5. Iger. (s.F.). Matematika Prvi semester Tacaná. Iger.
6. Jr. Geometrija. (2014). Poligoni. Lulu Press, Inc.
7. Miller, Heeren in Hornsby. (2006). Matematika: sklepanje in aplikacije (deseta izdaja). Pearson Education.
8. Patiño, m. (2006). Matematika 5. Uredništvo Progreso.
9. Wikipedija. Trapez. Okrevano od: je.Wikipedija.com