Laplace Transform

Kaj je Laplaceova preobrazba?

The Laplace Transform V zadnjih letih je bil velik pomen v inženirstvu, matematiki, fiziki, med drugimi znanstvenimi področji, saj poleg teoretičnega zelo zanimivega za teoretično preprost način za reševanje diferencialnih enačb, ki jih preoblikujejo v algebrske enačbe.

Prvotno Laplaceovo preobrazbo je v svoji študiji o teoriji verjetnosti predstavil Pierre-Simon Laplace (1745-1827), načeloma pa je bil obravnavan kot matematični predmet zgolj teoretičnega interesa.

Trenutne aplikacije nastanejo, ko so različni matematiki poskušali uradno utemeljiti "operativnim pravilom", ki jih uporablja Oliver Heaviside (1850-1925) pri preučevanju enačb elektromagnetne teorije.

Opredelitev Laplacea Transform

Naj bo F določena funkcija za t ≥ 0. Laplace Transform je opredeljen na naslednji način:

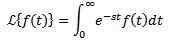
Pravi se, da Laplaceov preobrazba obstaja, če se prejšnji integral zbliža, sicer se reče, da Laplaceova preobrazba ne obstaja.

Na splošno označimo funkcijo, ki je želena preoblikovati drobne črke in kapitalska črka ustreza njegovi preobrazbi. Na ta način bomo imeli:

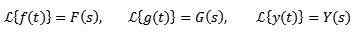
Primeri

Razmislite o konstantni funkciji f (t) = 1. Moramo preoblikovati:

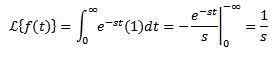
Pod pogojem, da se integral zbliža, to je pod pogojem, da je s> 0. Sicer s < 0, la integral diverge.

Naj g (t) = t. Njegovo Laplaceovo preobrazbo daje:

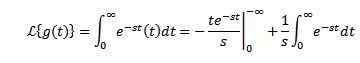
Pri integraciji po delih in to vedo^-ST Nagiba se na 0, ko se T nagiba k neskončnosti in s> 0, skupaj s prejšnjim primerom moramo:

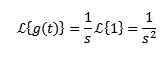
Transformal lahko ali ne obstaja, na primer za funkcijo f (t) = 1/t, integral, ki določa njegovo Laplaceovo preobrazbo.

Zadostni pogoji za zagotovitev, da Laplacea transformacije funkcije F obstaja, je, da je F v delih za t ≥ 0 neprekinjen in je eksponentnega vrstnega reda.

Govori se, da je funkcija v delih za t ≥ 0 neprekinjena, ko je za kateri koli interval [a, b] z a> 0 končno število točk t_k, Kjer ima F diskontinuitete in je neprekinjen v vsakem podintervalu [t_K-1,t_k].

Po drugi strani se reče, da je eksponentna funkcija c, če obstajajo resnične konstante m> 0, c in t> 0, tako da:

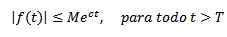
Kot primeri moramo f (t) = t² Je eksponentno, saj | t²| < e^3T Za vse t> 0.

Uradno imamo naslednji izrek:

Teorem (zadostni pogoji za obstoj)

Če je F neprekinjena funkcija za t> 0 in eksponentno C, potem obstaja Laplaceov transformacija za S> c.

Pomembno je poudariti, da je to pogoj zadostnosti, to je, da bi lahko obstajala, da obstaja funkcija, ki ne izpolnjuje teh pogojev, vendar njegova Laplasova preobrazba obstaja.

Primer tega je funkcija f (t) = t^-1/2 kar v delih ni neprekinjeno za t ≥ 0, vendar njegova Laplasova preobrazba obstaja.

Laplace transformacija nekaterih osnovnih funkcij

Naslednja tabela prikazuje Laplaceove preobrazbe najpogostejših funkcij.

Vam lahko služi: cele številke

Zgodovina Laplacea

Laplace Transform dolguje ime Pierre-Simon Laplacea, matematika in francoskega astronoma in teoretika, ki se je rodil leta 1749 in umrl leta 1827. Njegova slava je bila takšna, da je bil znan kot Newton v Franciji.

Leta 1744 je Leonard Euler (1707-1783) svoje študije posvetil integralom z obliko

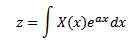
Kot rešitve navadnih diferencialnih enačb, vendar hitro opustijo to raziskavo. Kasneje je Joseph Louis Lagrange (1736-1813), ki je veliko občudoval Eulerja, tudi raziskal to vrsto integrala in jih povezal s teorijo verjetnosti.

1782, Laplace

Leta 1782 je Laplace začel študirati te integrale kot rešitve za diferencialne enačbe in po zgodovinarjih se je leta 1785 odločil, da bo preoblikoval težavo, ki je pozneje rodila Laplasove preobrazbe, kot jih danes razumejo.

Ko je bil uveden na področju teorije verjetnosti, je bil za znanstvenike trenutnega malo zanimiv in je bil obravnavan le kot matematični predmet samo teoretičnega interesa.

Heavside Oliver

Bilo je sredi devetnajstega stoletja, ko je angleški inženir Oliver Heavside odkril, da je mogoče diferencialne operaterje obravnavati kot algebrske spremenljivke, s čimer je dala svojo sodobno uporabo Laplaceom transformacijam.

Oliver Heaviside je bil fizik, angleški električni in matematični inženir, ki se je rodil leta 1850 v Londonu in umrl leta 1925. Medtem ko poskuša rešiti težave diferencialnih enačb, ki se uporabljajo za teorijo vibracij, in z uporabo študij Laplacea je začela oblikovati sodobne aplikacije Lapla Transforms.

Rezultati, ki jih izpostavlja težje širjenje.

Vendar pa je uporabnost dela Heavside pri reševanju fizičnih enačb povzročila, da so njihove metode priljubljene med fiziki in inženirji.

Kljub tem neuspehom in po nekaj desetletjih neuspešnih poskusov bi lahko na začetku 20. stoletja strogo utemeljilo operativna pravila, ki jih je določil Heaviside.

Ti poskusi so se izplačali zahvaljujoč prizadevanjem različnih matematikov, kot so Bromwich, Carson, Van der Pol.

Laplace transformacijske lastnosti

Med lastnostmi Laplace Transform izstopa naslednje:

Linearnost

Naj bosta C1 in C2 Constant in F (t) in G (t), katerih preobrazbe Laplace so F (s) oziroma G (s), potem mora:

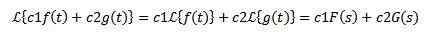
Zaradi te lastnosti pravijo, da je Laplace Transform linearni operater.

Primer:

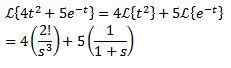
Prvi teorem za prevod

Če se zgodi, da:

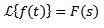
In 'A' je vsaka resnična številka, potem pa:

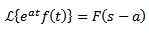
Primer:

Ko se Laplace de cos preoblikuje (2t) = s/(s^2 + 4), potem:

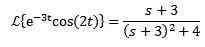
Drugi prevod teorema

Ja

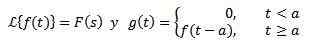
Tako

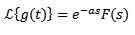
Primer:

Če je f (t) = t^3, potem f (s) = 6/s^4. In zato preobrazba 

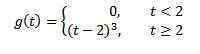
je g (s) = 6e^-2s/s^4

Sprememba obsega

Ja

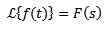
In 'a' je resnično drugačen od nič

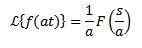
Primer:

Ker je transformacija f (t) = sen (t) f (s) = 1/(s^2 + 1)

Vam lahko služi: razvit zapis: kaj je, primeri in vaje

Laplace se je spremenil iz derivatov

Če f, f ', f ", ..., f^(N) So neprekinjene za t ≥ 0 in so eksponentne in f^(N)(t) je v delih za t ≥ 0 neprekinjeno

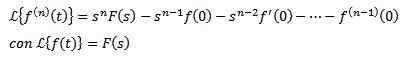
Integralna Laplace Transform

Ja

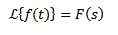
Tako

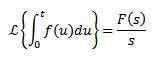
Množenje s tⁿ

Če moramo

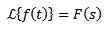
Tako

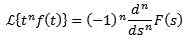
Divizija t

Če moramo

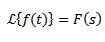
Tako

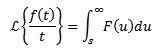
Periodične funkcije

Naj bo f periodična funkcija z obdobjem t> 0, torej f (t +t) = f (t), potem

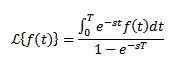
Vedenje f (s), ko se s nagiba k neskončnosti

Če je F neprekinjen v delih in eksponentnih vrsnih in

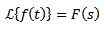
Tako

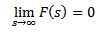
Inverzno preoblikovano

Ko uporabimo transformacijo Laplacea na funkcijo f (t), dobimo f (s), ki predstavlja omenjeno transformacijo. Na enak način lahko rečemo, da je f (t) preobrazba inverznega laplana f (s) in je napisana kot

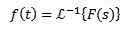
Vemo, da sta Laplace transformacije f (t) = 1 in g (t) = t f (s) = 1/s in g (s) = 1/s² zato moramo

Nekateri običajni preoblikovani Laplace so naslednje

Poleg tega je obratna transformacija LaPlace linearna, torej je izpolnjena

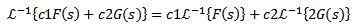
Vaja

Najti

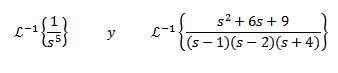
Za rešitev te vaje se moramo ujemati s funkcijo F (S) z nekaj prejšnje tabele. V tem primeru, če vzamemo n + 1 = 5 in uporabimo lastnost linearnosti povratne transformacije, pomnožimo in razdelimo po 4! Dobiti

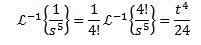
Za drugo inverzno preobrazbo uporabimo delne ulomke za prepisovanje funkcije f (s) in nato lastnost linearnosti, pri čemer pridobimo

Kot je razvidno iz teh primerov, je običajno, da se funkcija F (s), ki je ovrednotena. Za te primere je, kot je bilo ugotovljeno, dovolj, da funkcijo prepišete, dokler ne doseže ustrezne oblike.

Laplace Transform Applications

Diferencialne enačbe

Glavna aplikacija, ki jo ima Laplace Transforms, je reševanje diferencialnih enačb.

Z uporabo lastnosti transformacije izpeljanja je jasno, da

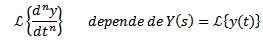
In od izpeljane N-1, ovrednotene pri t = 0.

Ta lastnost naredi preoblikovanje.

Naslednji primeri prikazujejo, kako uporabiti Laplace Transform za reševanje diferencialnih enačb.

Primer 1

Glede na naslednjo težavo začetne vrednosti

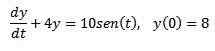
Uporabite Laplace Transform za iskanje rešitve.

Za vsakega člana diferencialne enačbe uporabimo transformacijo Laplacea

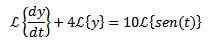
Za lastnost preobrazbe derivata, ki jo imamo

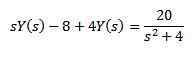
Pri razvoju vsega izraza in čiščenja in (e)

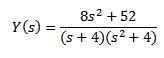
Z delnimi ulomki za prepisovanje desne strani enačbe dobimo

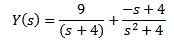
Končno je naš cilj najti funkcijo in (t), ki izpolnjuje diferencialno enačbo. Uporaba inverzne laplace Transform, ki jo ima za posledico

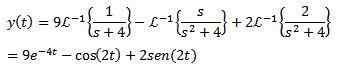
Primer 2

Rešiti

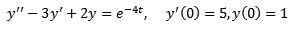
Kot v prejšnjem primeru uporabimo preoblikovano na obeh straneh enačbe in ločeno terminsko.

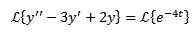
Na ta način imamo kot rezultat

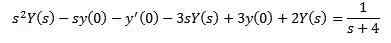
Zamenjava z začetnimi vrednostmi in čiščenjem in (S)

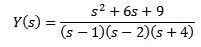
Z uporabo preprostih frakcij lahko napišemo, kako sledi enačba

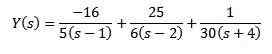
In uporaba obratne preobrazbe Laplacea kot rezultat

V teh primerih bi lahko dosegli napačen zaključek, da ta metoda ni veliko boljša od tradicionalnih metod za reševanje diferencialnih enačb.

Vam lahko služi: delež

Prednosti, ki jih ponuja transformacija Laplacea, je, da ni potrebna.

Poleg tega pri reševanju težav z začetno vrednostjo s to metodo od začetka uporabljamo začetne pogoje, zato ni treba izvesti drugih izračunov za iskanje določene rešitve.

Sistemi diferencialnih enačb

Laplace Transform se lahko uporabi tudi za iskanje rešitev hkratnih navadnih diferencialnih enačb, kot je prikazano v naslednjem primeru.

Primer

Rešiti

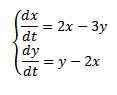
Z začetnimi pogoji x (0) = 8 e y (0) = 3.

Če moramo

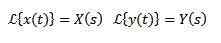
Tako

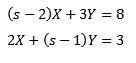
Reševanje nam daje rezultat

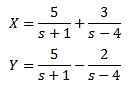
In pri uporabi obratne preobrazbe Laplacea imamo

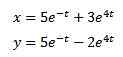
Mehanika in električna vezja

Laplace Transform je zelo pomemben pri fiziki, v glavnem ima aplikacije za mehaniko in električna vezja.

Preprosto električno vezje je sestavljeno iz naslednjih elementov:

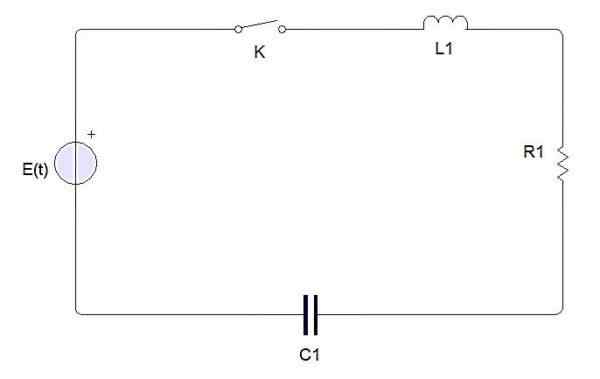Elementi električnega tokokroga

Stikalo, baterija ali vir, induktor, upor in kondenzator. Ko je stikalo zaprto, električni tok, ki ga označuje I (t). Obremenitev kondenzatorja je označena s Q (t).

Kirchhoffov drugi zakon mora biti napetost, ki jo proizvaja Fuente E do zaprtega vezja, enaka vsoti vsakega od napetosti.

Električni tok i (t) je povezan z nalaganjem q (t) v kondenzatorju skozi i = dq/dt. Po drugi strani je padec napetosti v vsakem od elementov opredeljen na naslednji način:

Padec napetosti v uporu je IR = R (dq/dt)

Padec napetosti v induktorju je l (di/dt) = l (d²Q/dt²)

Padec napetosti v kondenzatorju je Q/C

S temi podatki in uporabo Kirchhoffovega drugega zakona v preprostem preprostem vezju dobimo diferencialno enačbo drugega reda, ki opisuje sistem in nam omogoča, da določimo vrednost Q (T).

Primer

Induktor, kondenzator in upor so povezani z baterijo E, kot je prikazano na sliki. Induktor je 2 Henries, kondenzator 0,02 Farads in 16 OnHmios upornost. Trenutno t = 0 zapre vezje. Poiščite obremenitev in tok kadar koli t> 0, če je E = 300 voltov.

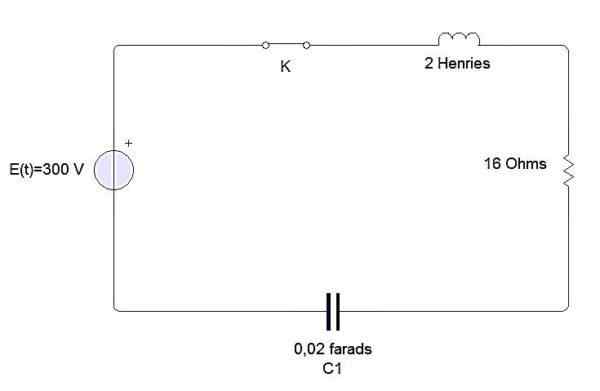
Imamo, da je diferencialna enačba, ki opisuje to vezje:

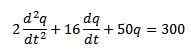
Kjer so začetni pogoji q (0) = 0, i (0) = 0 = q '(0).

Z uporabo transformacije Laplace to dobimo

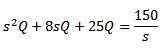
In čiščenje q (t)

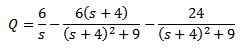
Nato uporaba inverzne transformacije Laplacea, ki jo imamo

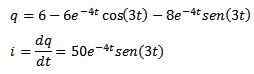
Reference

1. G.Holbrook, j. (1987). Laplace Transform za inženirje elektronike. Limusa.
2. Ruiz, l. M., & Hernandez, m. Str. (2006). Diferencialne in preoblikovane enačbe Laplacea z aplikacijami. Uredništvo UPV.
3. Simmons, g. F. (1993). Diferencialne enačbe z zgodovinskimi aplikacijami in opombami. McGraw-Hill.
4. Spiegel, m. R. (1991). Laplace se je spremenil. McGraw-Hill.
5. Zill, d. G., & Cullen, m. R. (2008). Diferencialne enačbe z vrednostmi vrednostnih papirjev na meji. Cengage učenje urejevalnikov, s.Do.