Toroid ali Toro Dona

Pojasnjujemo, kaj je bik ali bik, njegove značilnosti, volumen, površina, aplikacije in prikažejo več primerov

Kaj je toroid?

On Toroid Gre za tridimenzionalno geometrijsko telo v obliki obročev, prstana, prstana, krofa ali krofa, od tod tudi ime "Toro dona", ki pripada razredu imenovanih predmetov, imenovanih predmetov Revolucijske trdne snovi.

Toroid nastane z vrtenjem zaprte ravne figure, okoli črte, ki pripada isti ravnini slike, vendar ga ne prestreže, kot je prikazano spodaj:

Bik, ki je revolucijska površina, ki jo dobimo z vrtenjem zaprte ravne figure (kot oboda) okoli fiksne osi. Vir: Wikimedia Commons

Glavna značilnost toroida je, da ima, čeprav je zaprta površina, luknjo. To pomeni, da lahko dve točki njegove površine povežemo z segmentom, ki je zunaj predmeta.

Druga značilnost toroida je, da gre za tridimenzionalno figuro brez totov. Ta značilnost jo deli z drugimi volumetričnimi telesi, kot je sfera, toda čeprav je krogla konveksna površina, je bik hkrati konkaven in konveksn.

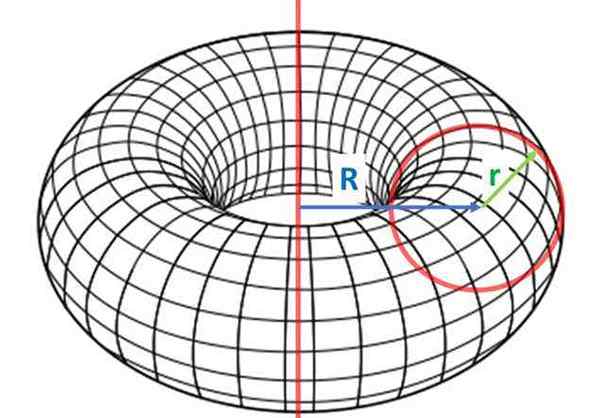
Med biki, bik Je najpogostejši in ga dobimo iz vrtenja radijskega kroga r, Glede osi razdalje R prvega. Radio R (v malih črko) je znan kot manjši polmer, R (kapital).

Volumen toroida

Bik nastane z vrtenjem zaprte ploščate površine Do okoli osi vrtenja, ki je ne reže. Označevanje z R Razdalja od osi do središča ravne figure je prostornina revolucijskega bika:

Vam lahko služi: inverzne trigonometrične funkcije: vrednost, derivati, primeri, vaje

V = 2πr⋅ a 

Ta rezultat se dobi pri uporabi Pappusov teorem Za količino trdne revolucije, ki navaja, da se volumen katere koli trdne revolucije dobimo tako, da pomnožimo območje figure, ki ga poruši obod, ki ga tvori vrtenje centroida (ali središče gravitacije ) vrtene figure, okoli osi vrtenja.

Zvezek bika

Bik je toroid, ki ga ustvarja radijski krog r. Če je razdalja osi vrtenja do središča vrtenega kroga R, je potem potrebno, da bi bik volumen:

V = (2πr) ⋅ (πr²) = 2π²R³

Površina bika

Bodite preprosto povezani ravni figuri Do in kontura L. Če se takšna številka zasuka okoli osi, ki je vsebovana v isti ravnini slike, vendar je to ne prečka, potem je ustvarjena površina območje:

S = 2πr⋅ l

Je razdalja od osi do središča gravitacije ali središča, na sliki Generatrix.

Ta rezultat je posledica Pappusov teorem Za površino revolucijske trdne snovi.

Površina bika

Krožni presek -sekcijski bik radia R (male črke) in radijski župan R (velike črke) je poseben bik, imenovan Toro.

Kot je kontura l kroga polmera r 2πr, Potem je območje površine omenjenega bika:

S = (2πr) ⋅ (2πr) = (4π²) (R⋅ r)

Toroidne aplikacije

Zaradi geometrijskih značilnosti ima bik nešteto praktičnih in kulturnih aplikacij. Za začetek so obročki ali obroči toroidni deli, ki imajo različne uporabe:

Vam lahko služi: minimalni kvadratki

Kulturno

• Okrasna ali kozmetična uporaba, ko je obroč nameščen na prst ali ko je prebadanje nameščen v uho.
• V nos volov je nameščen obroč, ki ga služi, da ga zaveže in nadzoruje.
• Ko je obroč ali obroč nameščen v levi roki na prstani način in material.

V mehaniki

Zunaj okrasnega, kozmetičnega in kulturnega konteksta ima bik veliko praktičnih aplikacij. V mehaniki se toroid uporablja kot zadrževalni obroč ležaja v konici osi vozila. 

Tudi ležaji motornih vozil sestavljajo en ali dva obroča v obliki bika z različnimi oblikami prereza, na katerih valjajo jeklenke ali krogle, z namenom zmanjšanja trenja v osi.

V električni energiji

V električnih aplikacijah je tudi toroid izjemnega pomena, saj imajo feromagnetna jedra induktorjev, elektromagerjev in transformatorjev pogosto obliko bika in na njih kabel v obliki tuljave.

Tokamak

Obstaja vrsta nadzorovanega fuzijskega reaktorja v obliki toroida ali krofa, ki ga imenuje rusko ime: tOkamak. Pri tej vrsti jedrskega fuzijskega reaktorja imata posoda in tuljave, ki proizvajajo magnetno polje plazemske zaprte.

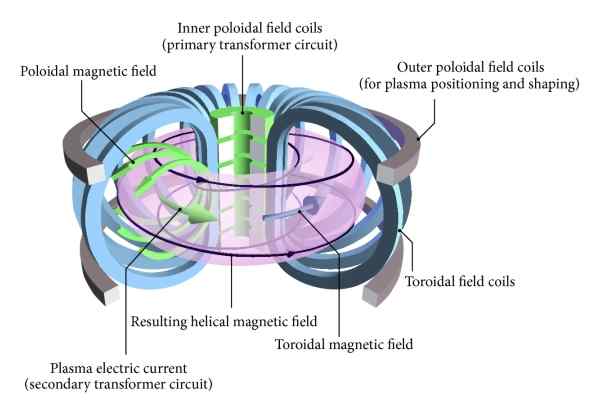Slika shematično prikazuje nadzorovan jedrski fuzijski reaktor v toroidni obliki, ki je znan kot "Tokamak". Pri tej vrsti reaktorja tako plazma, tuljave in magnetno polje zaprte imajo toroidno konfiguracijo. Vir: Wikimedia Commons

Primeri

Površina bika kvadratnega odseka (po formuli)

V tem primeru se šteje za bik kvadratnega odseka, kot je prikazano na naslednji sliki:

Vam lahko služi: Scaleno Triangle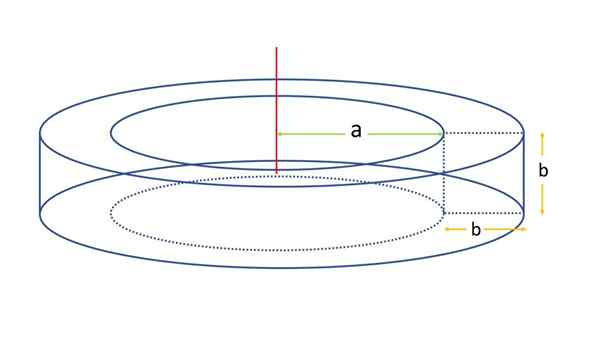 Kvadratni odsek Toroid. Vir: f. Zapata

Površina bo določena s pomočjo površinske formule za splošnega bika. V ta namen je treba vedeti razdaljo osi vrtenja do središča kvadrata, ki je z uporabo prejšnje nomenklature R:

R = a + b/2

Prav tako je treba vedeti obod L Slika Generatrix, ki je kot v tem primeru kvadrat na strani b, Njegova kontura bo dolga:

L = 4⋅B

Nato se uporabi površinska formula bika:

S = 2πr⋅l

Zamenjava R in L za ustrezne izraze, odvisno od ukrepov A in B kvadratnega bika, je:

S = 2π (a + b/2) ⋅4⋅B = 8π (a + b/2) ⋅B

Kvadratna površina toroida (vsota obrazov)

Kvadratni bik prejšnje figure je sestavljen iz štirih obrazov: zgornji in spodnji sta ploščata, notranjost in zunanjost pa valjasta.

Če upoštevamo to, je mogoče izračunati njegovo površino z dodajanjem površine štirih obrazov.

Zgornji in spodnji obraz ima območje, ki je enako območju zunanjega kroga polmera (A+B) manj kot notranjega kroga radia do, ki jih imajo kot rezultat:

S_s= S_Yo= π [(a+b)² - b²] = π⋅ [a²+ 2ab]

Notranji cilindrični obraz ima območje:

S₁= 2πab

In zunanji cilindrični obraz ima območje:

S₂= 2π (a+b) b = 2πab+2πb²

Tako da bo skupna površina toroida vsota_s+S_Yo+S₁+S₂:

A = 2π⋅ [a²+ 2ab]+2πab+2πab+2πb².