Vrste funkcij in njihovih grafov

Obstajajo raznoliki Vrste funkcij ki se uporabljajo za modeliranje problemov v vejah znanja, kot so naravoslovje, administracija, gospodarstvo in družbene vede. Matematično gledano je funkcija razmerje med dvema ali več spremenljivkami.

Velikokrat so med seboj povezani nekateri predmeti ali količine. Ti zneski so predstavljeni s spremenljivkami. Na primer, obstajata dve povezani spremenljivki, ki pripadata dvema nizama A in B, ne nujno številčna, čeprav sta večino časa-.

Če se šteje za funkcijo, mora to razmerje izpolnjevati dva pogoja: prvi je, da so vsi elementi začetnega niza sodelovanja, drugi pa, da je vsak element omenjenega nabora povezan samo z enim od elementov Set B.

Spremenljivke se običajno imenujejo s črkami x in in, z x kot neodvisna spremenljivka in in kot odvisna spremenljivka. Seveda jih lahko pokličemo na kakršen koli drug način in izberete ime spremenljivke v skladu z velikostjo, ki jo predstavlja.

Razmerje med obema je označeno s pismom F -ali še ena črka abecede in je predstavljena na več načinov, kot so nabor naročenih parov, graf, besedni izraz ali algebrska formula:

• f (x) = x + 1
• Prebivalstvo p določenega mesta v določenem časovnem intervalu t.
• H (x) = (1,3); (2,4); (3,5); (4.6)

Za funkcije je značilno, da imajo domena in domet ali pot. Domena je niz vrednosti, ki jih spremenljivka x Lahko vzamete, medtem ko je obseg nabor vrednosti, ki pridobi odvisno funkcijo ali spremenljivko in.

Razvrstitev funkcij

Funkcije je mogoče razvrstiti v 5 velikih kategorij, kot se odraža v naslednji shemi, v kateri je vsaka skupina označena z rimsko številko in barvo. Od leve proti desni se funkcije razvrstijo po:

• I) njegova oblika.
• Ii) simetrija.
• Iii) način izražanja spremenljivke.
• Iv) njena kontinuiteta in monotonost.
• V) način, kako so elementi domene povezani z elementi območja.

Glavna merila za klasifikacijo za funkcije. Vir: f. Zapata.

Zdaj sledite kratek opis vsake vrste funkcij z njihovimi primeri.

I) funkcije v skladu z njegovo obliko

Yo.1) Algebrske funkcije

So med najbolj uporabljenimi funkcijami na številnih znanosti, zato so najbolj znane. Za njih je značilno, da imajo kot pravilo dopisovanja algebrski izraz.

Algebrske funkcije so razdeljene na naslednje vrste:

• Yo.1.a) polinom ali polinom.
• Yo.1.b) racionalno.
• Yo.1.c) neracionalno.
• Yo.1.d) po odsekih.

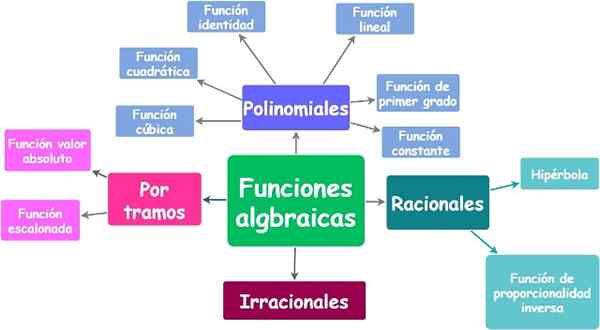Algebrske funkcije in njihove vrste. Vir: f. Zapata.

Yo.1.a) polinomne ali polinomne funkcije

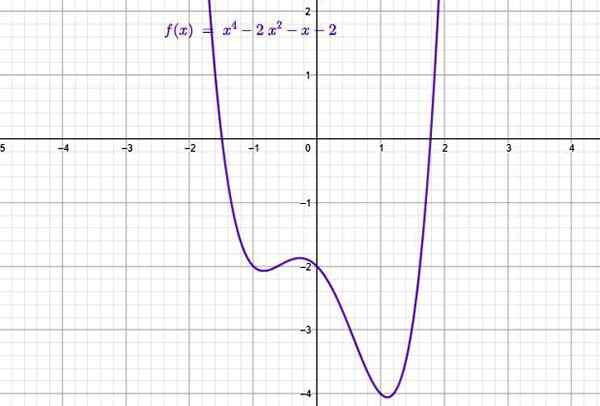Primer funkcije polinomnega tipa. Vir: f. Zapata skozi Geogebro.

Sestavljajo jih vsote izrazov, katerih splošna oblika je:

P (x) = a_nxⁿ + do _N-1x^N-1 +… Do₁x + a₀

Kjer koeficienti_n, do _N-1… Do₁, do₀ So resnične številke in n je celo število. Domena polinomnih funkcij je nabor realnih številk in so tudi neprekinjene funkcije v celotni domeni.

Na zgornji sliki je graf naslednje polinomne funkcije vrstnega reda 4:

f (x) = x⁴ - 2x² - x -2

Med polinomnimi funkcijami se razlikujejo nekateri posebni primeri glede na vrednosti koeficientov. Vredno je razmisliti o previdno, saj so zelo koristne v več situacijah:

i) konstantna funkcija

Obstaja stalna funkcija, kadar so vsi koeficienti preklicani, razen₀:

f (x) = a₀ = k

Graf konstantne funkcije je ravna črta vzporedna z vodoravno os, kot so črte:

• f (x) = 2
• g (x) = π
• H (x) = -3/2

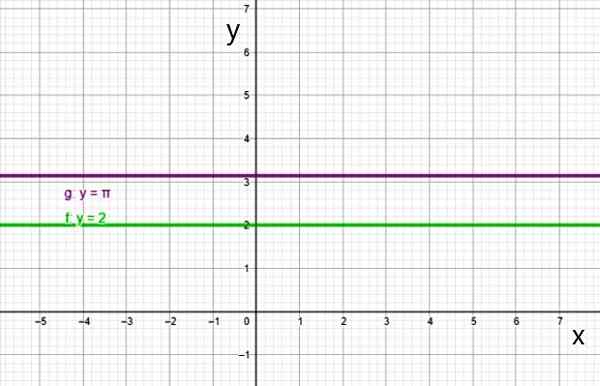Dva primera konstantne funkcije. Vir: f. Zapata.

Ii) funkcija prve stopnje

Prva funkcija ali povezana funkcija je tista, katere graf je ravna črta. To je poseben primer polinomne funkcije, kjer so vsi koeficienti urejenosti₁ že₀. Daje ga:

f (x) = a₁x + a₀

Vrednost a₁ To je naklon črte, ki daje mero naklona in₀ Je rez črte z navpično osi. Oba lahko vzameta pozitivne ali negativne vrednosti.

Primeri funkcije prve stopnje so naslednji:

• G (x) = 2x -1
• H (x) = -6x +5/2

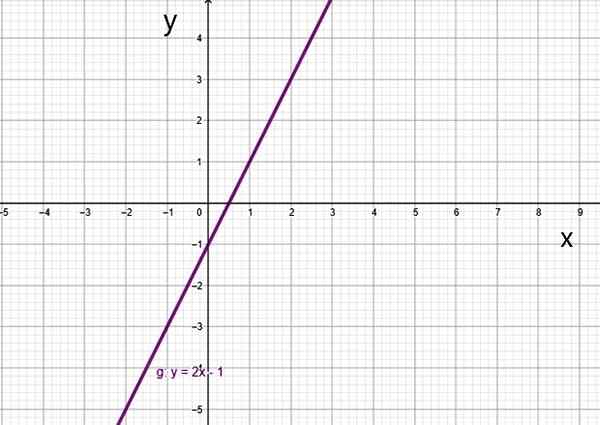Funkcija prve stopnje f (x) = 2x-1. Vir: f. Zapata.

Obstaja poseben primer, ki je linearna funkcija.

Lahko vam služi: Ukrepi za osrednje tendence za združene podatke: formule, vaje

iii) linearna funkcija

Ko koeficient₀ Je 0, funkcija vedno poteka skozi izvor in se izraža s f (x) = a₁X, klicanje Linealna funkcija, Kako si:

• f (x) = 5x
• G (x) = -7x

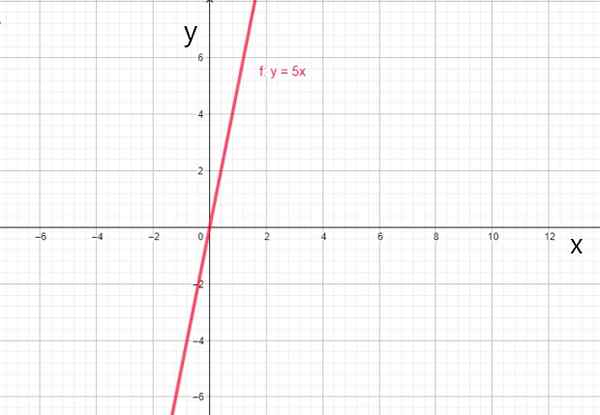Linearna funkcija f (x) = 5x. Vir: f. Zapata.

iv) Funkcija identitete

Je poseben primer linearne funkcije, v kateri₁ = 1:

f (x) = x

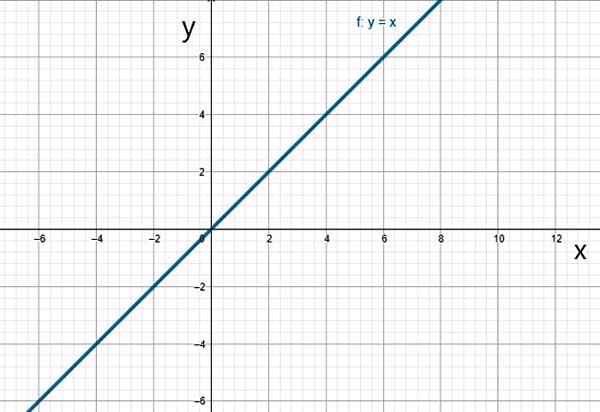Funkcija identitete. Vir: f. Zapata.

v) kvadratna funkcija

Ima splošno obliko:

f (x) = a₂x² +do₁x + a₀

Z₂  ≠ 0.

Njegov graf je prispodoba, katere osna ali simetrična os je vzporedna z osi ordinatov. Vedno seka navpično osi v koordinatni točki x = 0, y = a₀. Kar zadeva križišča z vodoravno osi, ima lahko do največ 2.

Primeri kvadratnih funkcij so:

• f (x) = x² - 3x - 4
• G (x) = 4x²
• H (x) = x²-1

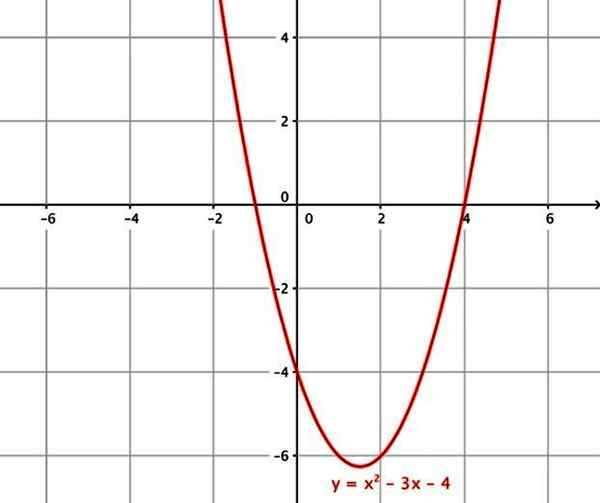Kvadratna funkcija. Vir: Wikimedia Commons.

vi) kubična funkcija

Kot že ime pove, kubična funkcija vsebuje moč 3:

f (x) = a₃x³ + do₂x² + do₁x + a₀

Koeficient a₃ Vedno se razlikuje od 0, kot v teh primerih:

• f (x) = x³
• G (x) = 5x³ - 2
• H (x) = -3x³ + 4x² + 10x + 1

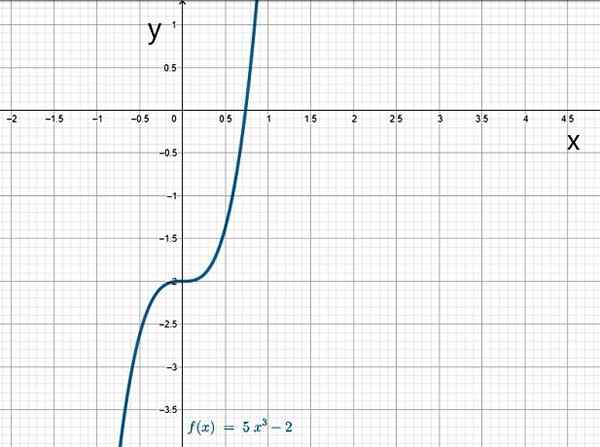Kubična funkcija. Vir: f. Zapata.

Yo.1.b) racionalne funkcije

Racionalne funkcije imajo obrazec:

 Kjer sta p (x) in q (x) nepopustljivi polinomi, to je, da nimajo skupnega dejavnika in v vsakem primeru Q (x) ≠ 0.

Iz domene racionalnih funkcij so vse vrednosti, ki razveljavijo imenovalec q (x), torej njegove korenine, medtem ko vrednosti vrednosti vrednosti in ki določajo vodoravne asimptote.

Asymptote je črta, na katero se približuje funkcija, tako na levi kot na desni, zgoraj ali spodaj, vendar nikoli ne prečka. Takšne črte so lahko navpične, vodoravne ali nagnjene.

Primeri racionalnih funkcij so:

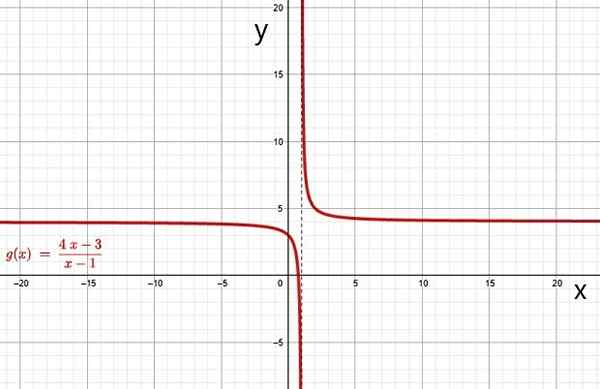Racionalna funkcija. Vir: f. Zapata skozi Geogebro.

i) hiperbola

Graf racionalne funkcije je hiperbola, kadar ima polinom v imenovalcu Q (x) 1. razred. Graf funkcij f (x) in g (x) zgornjih primerov sta hiperbola, enostavno ga je mogoče preveriti prek brezplačne spletne grafične programske opreme, kot je geogebra.

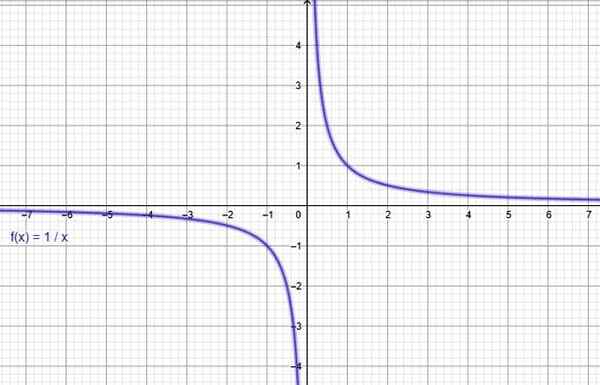Funkcija y = 1/x. Vir: f. Zapata skozi Geogebro.

Ii) funkcija inverzne proporcionalnosti

Je funkcija oblike:

Kjer je C resnično število, ki se razlikuje od 0. Njegova domena je nabor resničnih številk, razen 0.

Yo.1.c) iracionalne funkcije

So tisti, katerih neodvisna spremenljivka je pod radikalnim znakom. Njegova splošna oblika je:

Nekatere od teh funkcij so lahko:

• 
• 

Domena teh funkcij je določena na naslednji način:

-Če so korenine indeksa navora, mora biti subradični znesek f (x) vedno 0 ali pozitiven.

-Kadar so korenine čudne, je F (x) lahko pozitiven ali negativen. Zato so v tem primeru domena funkcije realne številke.

Na primer domena:

Je nabor realnih števil, tako da je X-3 večji ali enak 0. V tem primeru mora biti X večji ali enak 3. Zato je domena te funkcije niz vrednosti intervala [3, ∞+).

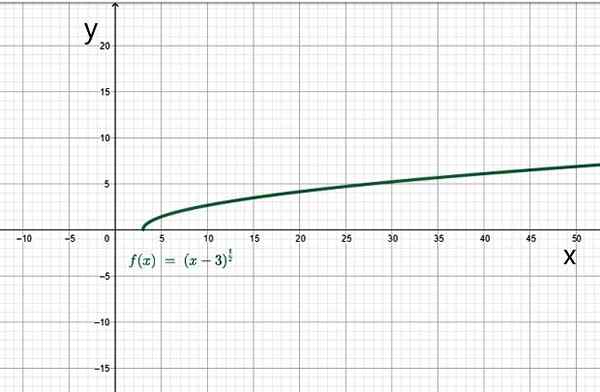 Primer iracionalne funkcije. Vir: f. Zapata.

Yo.1.d) funkcije na koščke ali po odsekih

Funkcija v delih, po razdelkih ali delih je tista, ki za različne vrednosti domene zahteva več kot eno formulo. Tu je nekaj primerov vaše prijave:

-Cene za pošiljanje paketov po pošti, odvisno od teže ali glasnosti, izvora in cilja istega.

-Stopnje za storitve, na primer telefonijo in elektriko.

-Prodaja vstopnic za muzeje ali zabaviščne parke, odvisno od starosti.

V matematični obliki je lahko funkcija v delih na primer:

Domena funkcije v delih je odvisna od njegove definicije. V prejšnjem primeru je domena nabor, ki ga tvori: (-∞, -1) ∪ [1,+∞).

Funkcija absolutne vrednosti. Vir: f. Zapata skozi Geogebro.

Ii) funkcija Escalonada

Graf te funkcije po odsekih je sestavljen iz korakov, na primer lestve ali je lahko različnih višin, odvisno od načina definiranja funkcije.

Lahko vam služi: Hipparco of Nicea: Biografija in prispevki za znanost

Za to je izbran končni interval [a, b], ki vsebuje določeno končno število prekinitev, imenovano x_Yo < x₁ < x₂ <… . x_n  In izbran je odprt interval (x_Yo , x_i+1) Dati konstanto vrednosti s_Yo, S skoki na točkah x_Yo. Vrednost S_Yo To je višina zadevnega koraka.

Primer zamaknjene funkcije je celoten del, ki prevzame katero koli število in ga povezuje z naslednjim celotnim celotnim celotnim ali privzetim ali privzetim. Sledi celoten del:

[x] = (večje celo število ≤ x)

V skladu s to funkcijo je celoten del 2.5 je:

[2.5] = (večje celo število ≤ 2.5) = 2

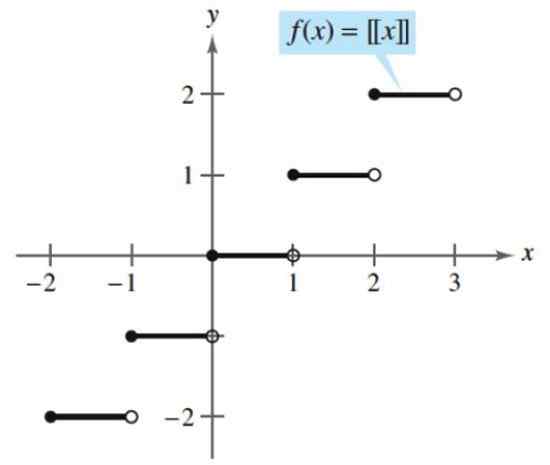Celoten del. Vir: Larson, r. Izračun z analitično geometrijo. McGraw-Hill.

Yo.2) transcendentne funkcije

Ne -algebrske funkcije se imenujejo transcendentni. Eksponentne, logaritmične in trigonometrične funkcije so transcendentne funkcije.

V njih spremenljivka x Je del argumenta funkcije ali kot del eksponenta ali indeksa nekega korena:

• f (x) = log (x+1)
• H (x) = -0.2⋅8^-3x

Transcendentne funkcije imajo veliko aplikacij, na primer pri preučevanju vibracij in valov, porazdelitve verjetnosti, modeliranju valov, rasti raznolikega populacije, radioaktivnih razpada, obrestnih mer in številnih drugih. 

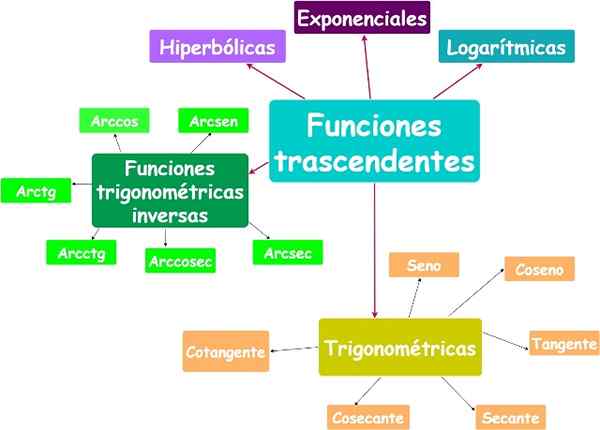Glavne transcendentne funkcije. Vir: f. Zapata.

Yo.2.a) eksponentna funkcija 

Eksponentna funkcija je opredeljena z:

f (x) = a^x

Kjer je a osnova, ki je vedno pozitivno število 1, in spremenljivka, resnično število, se pojavi v eksponentu. Na splošno je napisana eksponentna funkcija:

f (x) = a⋅A^Bx

Tu sta A in B resnični koeficienti. Sledijo funkcije te vrste:

• f (x) = 5e^x
• H (x) = 4. 10^5x
• g (t) = 8e^-2T

Baza in, kje in To je število Eulerja 2.71828 ... se pogosto pojavlja v težavah znanosti in inženiringa, pa tudi statistike. Ko se funkcija imenuje ta osnova Naravna eksponentna funkcija.

Domena eksponentne funkcije je niz realnih števil, medtem ko je obseg pozitivne številke.

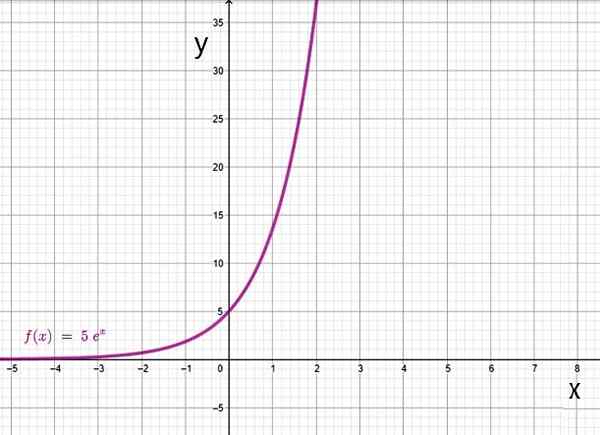Eksponentna funkcija, ki temelji na. Vir: f. Zapata skozi Geogebro.

Yo.2.b) Funkcija logaritma

Funkcija logaritma, ki temelji na svojem delu do To je obratna funkcija eksponentne funkcije, ki temelji na do. Ja:

dnevnik_do x = y

Tako:

x = aⁱⁿ

Zlasti, če je osnova logaritma številka E, se funkcija imenuje Funkcija neperijskega logaritma In je označen kot ln. Funkcije te vrste so:

• f (x) = ln x
• g (x) = log (x+1)
• H (t) = 1 - dnevnik x²

Domena funkcije logaritma, ne glede na osnovo, so pozitivne realne številke, ne vključno z 0. To pomeni, da ni logaritmov negativnih številk ali 0.

Vendar je lahko logaritem 0 ali negativen: logaritem številke med 0 in 1 je negativen in doseže svoj del_do 1 = 0.

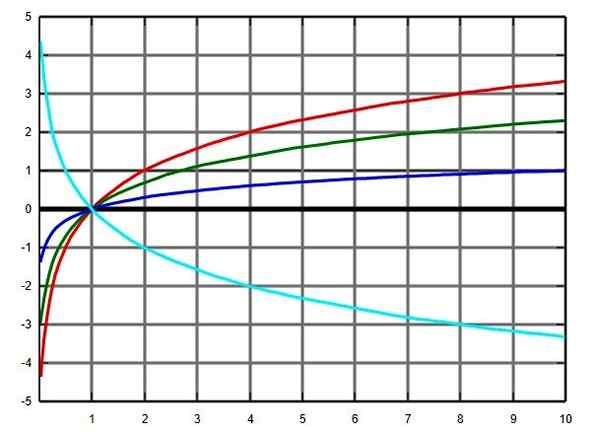Graf funkcije logaritma v več podlagah: podstavek 2 v rdeči, zeleni E, modri bazi in turkizni na podlagi 0.5. Vir: Wikimedia Commons.

Yo.2.c) Trigonometrične funkcije

To so tisti, ki prihajajo iz trigonometričnih razlogov: sinus, kosinus, tangent, sušenje, harmoniranje in soglasje kota x. Označeni so kot:

Sen X, Cos X, TG X, Sec X, Harm X in Cotg X

To so periodične funkcije, kar pomeni, da je njegova oblika ponavljajoča, zato so zelo koristne za opis naravnih pojavov, kot so signali, nihanja, krožno gibanje in premiki nihanja, za katere je značilna ponavljanje.

Primeri trigonometričnih funkcij so:

• f (x) = sin x
• G (t) = 5⋅cos (ωt + π)
• H (x) = tg (x/2)

Spremenljivka x je izražena v radianih.

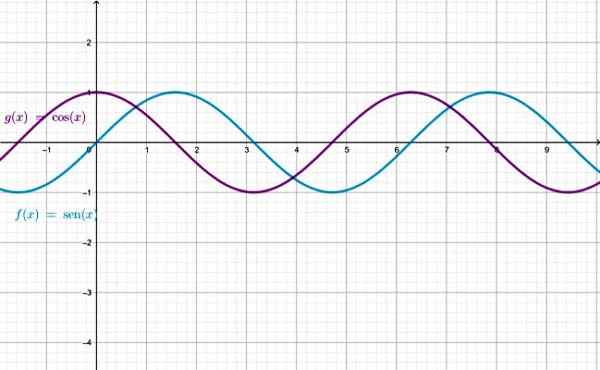Graf funkcij Sen X in Cos X, upoštevajte, da sta enaka, le da je ena razseljena glede na drugo. Vir: f. Zapata skozi Geogebro.

Obvladovanje funkcij sena x in cos x je nabor resničnih številk. Za preostale funkcije obstajajo vrednosti X, za katere funkcija ni definirana:

-Funkcija TG X ne obstaja, kadar je x = ± π /2, ± 5π /2 ... to je, vse nenavadne večkratne množice π /2.

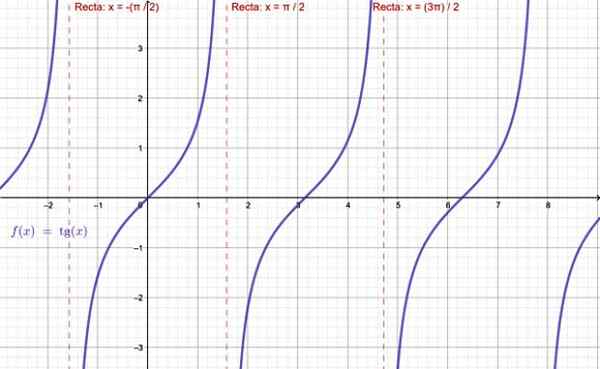Grafiranje tangentne funkcije. Vir: f. Zapata skozi Geogebro.

-Kar zadeva f (x) = cotg x, ta funkcija ni definirana za celotne množice π: ± π, ± 2π, ± 3π ..

Vam lahko služi: zakon znakov

-Funkcija y = sec x ni veljavna, kadar cos x = 0, ki izključuje x = ± π /2, ± 5π /2… njene domene.

-Končno za f (x) = škoda x.

Yo.2.d) hiperbolične funkcije

Hiperbolične funkcije so posebne kombinacije eksponentnih in^x in e^-x In imenujejo jih kot naroč, Coseno .. .hiperbolična. Tako kot pri trigonometričnih funkcijah, imenovanih tudi "krožni", je tudi 6 hiperboličnih funkcij:

-Hiperbolični sinus Senh x:

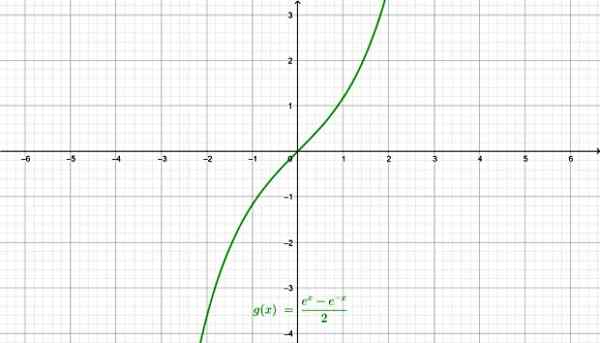Funkcija hiperboličnega sinusa. Vir: f. Zapata skozi Geogebro.

-Hiperbolični kosinus COSH X:

 -Hiperbolična tangenta tanh x:

 -Hiperbolično kombajn CSCH X:

 -Hiperbolični sekat Sec X:

-Hiperbolični kotangent COTH X:

Prilagodljiv kabel, narejen iz enotnega in visečega materiala med dvema točkama, ima obliko krivulje Katenar, ki je izražen kot hiperbolični kosinus:

Yo.2.e) Inverzne trigonometrične funkcije

Ustrezajo obratnim trigonometričnim funkcijam. Na primer, kakšen bi bil kot (lok), katerega naroč je vreden 0.5?

Odgovor je Arc Sen 0.5, ki se glasi »ločni sinus 0.5 ”, in ta kot je 30 °, čeprav načeloma to ne bi bil edini kot, katerega naročje je vredno 0.5, saj je funkcija sen x periodična. Kar se zgodi, je, da če se funkcija Sen X izvaja v celotni domeni, ne bi imela obratne, zato funkcije Arcoseno ni bilo mogoče določiti. Težava je rešena tako, da vse omejimo na kote med -π/2 in +π/2.

To je mogoče izraziti na naslednji način:

Če je lok sen x = θ, to pomeni, da greh θ = x

Z -π/2 ≤ θ ≤ π/2.

Druga zapis, ki se uporablja za lok sen x, je f (x) = greh^-1 x. Graf je prikazan spodaj:

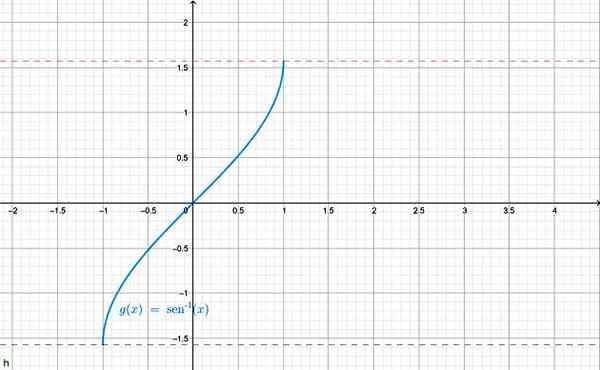Arcsen X Function Graphics. Vir: f. Zapata skozi Geogebro.

Za druge trigonometrične funkcije je mogoče določiti tudi obratno, na primer: lok cos x = θ in s tem. Za vsakega je rang pravilno omejen, da je obratna ustrezna trigonometrična funkcija.

Ii) funkcije v skladu z njegovo simetrijo

Ii.1) Par

Če je za vse x, ki pripada domeni f (x), izpolnjeno:

f (x) = f (-x)

Govori se, da je funkcija enakomerna kot tista, ki sledijo:

• f (x) = x² - 3
• g (x) = cos x
• 

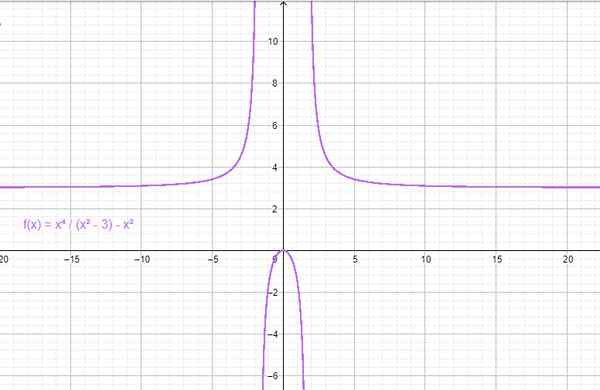  Primer funkcije para. Vir: f. Zapata skozi Geogebro.

Na primer, delam x = 1 in f (x) = x² - 3 je pridobljeno:

f (1) = 1² - 3 = -2.

In če x = -1, potem:

f (-1) = (-1)² - 3 = -2.

Oba rezultata sta enaka.

Tudi funkcije imajo simetrijo okoli navpične osi, kot je razvidno iz prejšnje slike.

Ii.2) Neparna funkcija

Po drugi strani pa, da:

f (-x) = -f (x)

Funkcija je čudna.

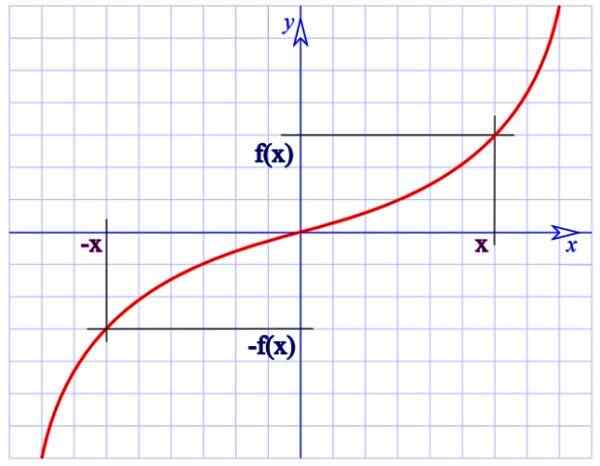Nenavadna funkcija. Vir: Wikimedia Commons.

Na primer funkcija f (x) = 1/x zgornje figure je neparna, saj:

f (-x) = -1/x

In

-f (x) = -1/x

Druga pomembna funkcija Impar je f (x) = sin x.

Upoštevajte, da imajo ned.

Iii) delovanje v skladu z izrazom spremenljivke

Iii.1) Izrecne funkcije

Izraženi so neposredno v smislu odvisne spremenljivke, kot je y = f (x). Na primer:

• f (x) = x³

Iii.2) Implicitne funkcije

V implicitnih funkcijah se nobena od spremenljivk ne zdi jasna. Izraženi so kot f (x, y) = 0, na primer:

• x² + in² -3xy = 0
• xy = - x²+ X-5

Funkcije, opisane v tem članku, so eksplicitne funkcije.

Iv) funkcije v skladu z vašo grafiko

Glede na njihov graf so lahko funkcije neprekinjene ali prekinjene. Neprekinjene funkcije je mogoče zaslediti, ne da bi prekinili možgansko kap, na drugi strani pa diskontinuirane funkcije predstavljajo skoki. Na naslednji sliki je funkcija prekinjena pri x = a:

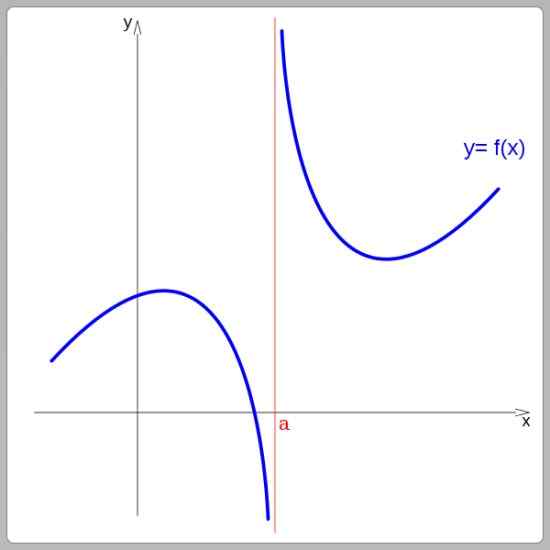Funkcija prekinitve pri x = a. Vir: Wikimedia Commons.

Primeri neprekinjenih funkcij so linearna funkcija, kvadratna funkcija ter sinusne in kosinusne funkcije. In med diskontinuiranimi funkcijami sta zamaknjena funkcija in tangentna funkcija.

V) Funkcije glede na razmerje med elementi domene in območjem

V.1) Injektivna funkcija

Funkcija je Injektivno Kadar v začetnem ali domeni ni dveh različnih elementov, ki imata isto sliko v nastavitvi prihoda.

Recimo, da imajo resnične funkcije na primer, če ni drugače določeno:

f (x) = 5x -2

Vsa vrednost x, ki pripada domeni f (x), ki je niz ℛ resničnih številk, ima edinstveno, tudi resnično sliko. Po drugi strani pa v tej drugi funkciji:

g (x) = x²

V domeni obstajajo različni elementi, ki imajo isto sliko, na primer x₁= 2 in x₂= -2:

G (2) = g (-2) = 4.

Način za prepoznavanje injektivne funkcije iz njegovega grafa je risanje vodoravne črte, če jo razrežemo na krivuljo v več kot eni točki.

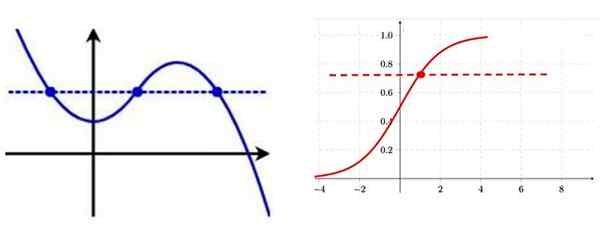Na levi funkciji UN injektivne funkcije upoštevajte, da je več točk grafa z isto navpično koordinato. Na desni injektivni funkciji ima na vsaki točki krivulje določeno "Y" koordinato. Vir: f. Zapata.

V.2) Prekomerna funkcija

V Obitne funkcije, Vsi elementi nabora prihodov so podoba nekega elementa začetnega niza. Primer prekomerne funkcije je enak f (x) = 5x -2, vendar g (x) = x² Ni, saj so vrednosti, vzete G (x), le pozitivne resnične in 0.

Vendar bi lahko domeno na novo definirali tako, da je bil G (x) prekomerni, če se na primer spremeni v vse pozitivne resnične plus 0. 

V.3) Bijektivna funkcija

Končno se imenuje funkcija, ki je hkrati injektivna in prekomerna Bijective. Primeri bijektivnih funkcij so: povezana funkcija, eksponentna funkcija in funkcija logaritma.

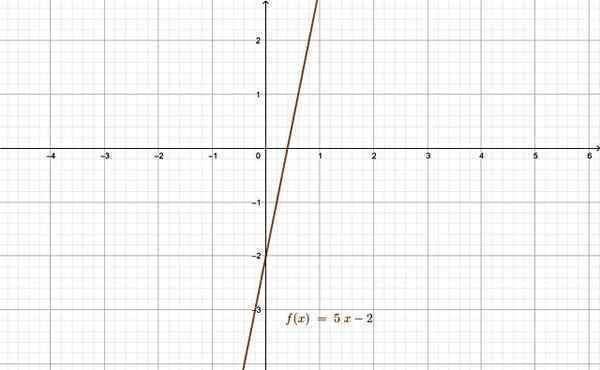Povezana funkcija je dober primer bijjektivne funkcije. Vir: f. Zapata skozi Geogebro.

Reference

1. Cona e-math. Vrste funkcij. Okreval od: emathzone.com.
2. Hoffman, J.G. Izbira vprašanj matematike. Ed. Sphinx.
3. Matematika je zabavna. Commons deluje referenca. Okreval od: MathisFun.com.
4. Requena, b. Formule vesolja. Vrste funkcij. Okrevano od: univerzeformulas.com.
5. Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.