Varignon teorem

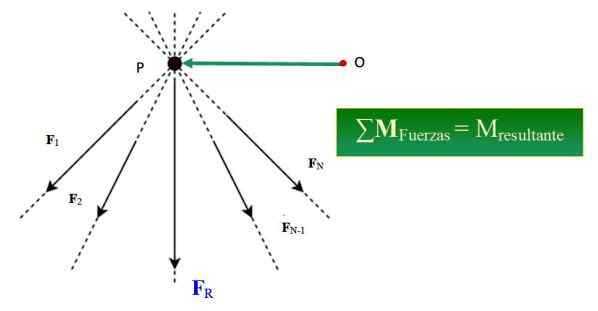
Slika 1.- Varignonov teorem potrjuje, da je vsota trenutka sil okoli določene točke enakovredna času rezultata glede na to točko. Vir: Wikimedia Commons/F. Zapata.

Kaj je Varignonov teorem?

Varignonov teorem v mehaniki navaja, da je vsota trenutkov, ki jih ustvari sistem sočasnih sil glede na določeno točko, enaka trenutku nastale sile glede na isto točko.

Zaradi tega je ta izrek znan tudi kot Začetek trenutkov.

Medtem ko je bil prvi, ki je navedel Nizozemca Simon Stevin (1548-1620), ustvarjalec hidrostatičnega paradoksa, francoskega matematika Pierra Varignon (1654-1722) je bil tisti, ki mu je pozneje dal svojo dokončno obliko.

Primer, kako deluje Varignonov teorem v mehaniki, je naslednji: predpostavimo, da preprost sistem dveh koplanarov in sočasnih sil deluje na točko F₁ in F₂, (Označeno s krepko za svoj vektorski značaj). Te sile povzročajo mrežo ali posledično silo, imenovano F_R.

Vsaka sila izvaja navor ali trenutek glede na točko ali, ki ga izračuna vektorski produkt med vektorjem položaja r_Op in matrica F, kje r_Op Usmerjena je iz ali do točke soglasja P:

M_O1 = r_Op × F₁

M_O2 = r_Op × F₂

Glede na F_R = F₁ + F₂, tako:

M_Tudi = r_Op × F₁ + r_Op × F₂ = M_O1 + M_O2

Ampak kako r_Op To je pogost dejavnik, ki uporablja distribucijsko lastnost za navzkrižni izdelek:

M_Tudi = r_Op × (F₁ + F₂) = r_Op × F_R                

Zato je vsota trenutkov ali navorov vsake sile glede na točko ali je enakovredna času nastale sile glede na isto točko.

Izjava in demonstracija

Biti sistem n sočasnih sil, ki jih oblikuje F₁, F₂, F₃.. F_N, katerih linije delovanja so namenjene točki P (glej sliko 1), trenutek tega sistema sil M_Tudi, Glede točke ali je podana:

Vam lahko služi: nestabilno ravnovesje: koncept in primeri

M_Tudi = r_Op × F₁ + r_Op × F₂ + r_Op × F₃ +.. r_Op × F_N = r_Op × (F₁ + F₂ + F₃ +.. F_N)

Demonstracija

Za prikaz teorema je narejena distribucijska lastnost vektorskega izdelka med vektorji.

Biti sile F₁, F₂, F₃.. F_N Uporablja se za točke na₁, Do₂, Do₃… Do_N in sočasno v točki P. Nastali trenutek tega sistema glede na točko ali imenovano M_Tudi, To je vsota trenutkov vsake sile glede na to točko:

M_Tudi = ∑ r_Oai × F_Yo

Kadar vsota gre od i = 1 do i = n, saj je N sil. Ker so to sočasne sile in ker je vektorski izdelek med vzporednimi vektorji ničen, se zgodi, da:

r_Pai × F_Yo = 0

Z ničelnim vektorjem, označenim kot 0.

Trenutek ene od sil v zvezi z O, na primer sila F_Yo Uporablja se v a_Yo, Napisano je tako:

M_{slišal sem} = r_Oai × F_Yo

Vektor položaja r_Oai  Lahko se izrazi kot vsota položaja dveh vektorjev:

r_Oai = r_Op + r_Pai

Na ta način trenutek glede ali sile F_Yo je:

M_{slišal sem} = (r_Op + r_Pai) × F_Yo = (r_Op × F_Yo) + (r_Pai × F_Yo)

Toda zadnji izraz je ničen, kot je razloženo zgoraj, ker r_Pai je na liniji delovanja F_Yo, Zato:

M_{slišal sem} = r_Op × F_Yo

Vemo, da je trenutek sistema v zvezi s točko ali je vsota vseh posameznih trenutkov vsake sile glede na to točko, potem:

M_Tudi = ∑ M_{slišal sem} = ∑ r_Op × F_Yo

Kot r_Op Konstantno je iz vsote:

M_Tudi = r_Op × (∑ F_Yo)

Toda ∑ F_Yo To je preprosto posledična mreža ali sila F_R, Zato je takoj sklenjeno, da:

Vam lahko služi: leyden steklenica: deli, delovanje, poskusi

M_Tudi = r_Op × F_R

Primer

Varignonov teorem olajša izračun trenutka sile F Glede točke ali strukture, prikazane na sliki, če je sila razčlenjena na njegove pravokotne komponente in se izračuna trenutek vsakega od njih:

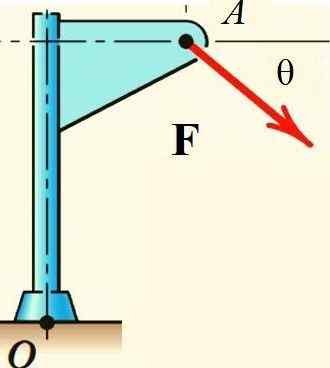Slika 2.- Varignonov teorem velja za izračun trenutka sile okoli oz. Vir: f. Zapata.

Aplikacije iz teorema Varignon

Ko je znana sila, ki izhaja iz sistema, lahko uporabimo Varignonov izrek.

Če je sistem sestavljen iz sil na isti ravnini in točke glede na to, v katero želite izračunati trenutek, ki pripada tej ravnini, je nastali trenutek pravokoten.

Na primer, če so vse sile v ravnini xy, je trenutek usmerjen na osi z.

V tem primeru Varignonov teorem omogoča izračun trenutka, ki je posledica sistema skozi seštevanje. Zelo je uporaben v primeru sistema treh dimenzionalnih sil, za katerega smer nastalega trenutka ni znana a priori.

Za reševanje teh vaj je priročno.

Vaja rešena

Z Varignonovim teoremom izračunajte trenutek sile F okoli točke ali prikazano na sliki, če je velikost F 725 n.

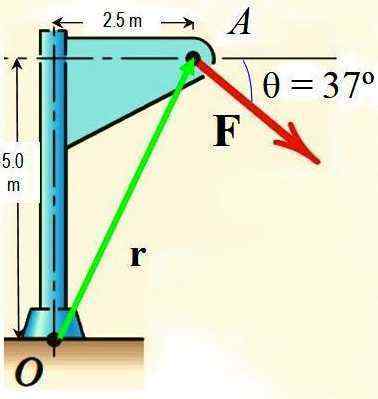Slika 3.- Slika za reševanje vaje. Vir: f. Zapata.

Rešitev

Za uporabo Varignonovega teorema se razpade sila F v dveh komponentah, katerih trenutki naokoli ali so izračunani in dodani, da dobimo nastali trenutek.

Vam lahko služi: togo telo

F_x = 725 N ∙ cos 37 º = 579.0 n

F_in = - 725 N ∙ Sen 37 º = −436.3 n

Podobno je vektor položaja r usmerjena iz ali v A ima komponente:

r_x = 2.5m

r_in = 5.0 m

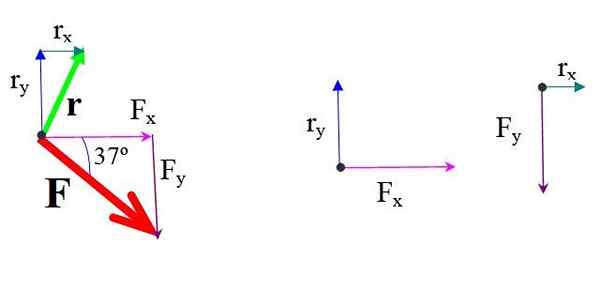Slika 4.- Komponente sile in položaja. Vir: f. Zapata.

Trenutek vsake komponente sile glede na ali se pomnoži silo in pravokotno razdaljo.

Obe sili ponavadi vrtita strukturo v isti smeri, kar je v tem primeru smisel za oceno, ki je poljubno dodeljen pozitivni znak:

M_Vol = F_x∙ r_in ∙ greh 90 ° = 579.0 N ∙ 5.0 m = 2895 n ∙ m

M_Oy = F_in∙ r_x ∙ Sin (−90 °) = −436.3 N ∙ 2.5 m ∙ (−1) = 1090.8 n ∙ m

Nastali trenutek glede ali je:

M_Tudi = M_Vol + M_Oy = 3985.8 n ∙ m pravokotno na ravnino in v navoru.

Reference

1. Bedford, 2000. Do. Mehanika za inženiring: statična. Addison Wesley. 
2. Pivo, f. 2010. Statična. McGraw Hill. 9na. Izdaja.
3. Hibbeler, R. 1992. Mehanika za inženirje. 6. Izdaja. CECSA.
4. HK Engineering. Varignon teorem. Obnovil od: YouTube.com.
5. Wikipedija. Varignonov teorem (mehanika). Pridobljeno iz: v.Wikipedija.org.