Zeleni teorem, demonstracije, aplikacije in vaje

On Zeleni teorem Gre. Vključene funkcije morajo biti označene kot vektorska in določena polja znotraj poti c.

Na primer, izraz integralne črte je lahko zelo zapleten za reševanje; Vendar pa pri izvajanju Green -ovega teorema dvojni integrali postanejo precej osnovni. Vedno je pomembno spoštovati pozitiven občutek poti, to se nanaša na smer igle ure.

Green's Teorem je poseben primer Stokesovega teorema, kjer se projekcija vektorske funkcije izvaja v ravnini XY.

[TOC]

Opredelitev

Green -ov izraz Green -ovega teorema je naslednji:

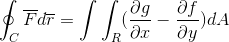
V prvem mandatu opazimo črto integral, ki jo definira usmeritev "c", iz produkta skalarja med vektorsko funkcijo "f" in funkcijo vektorja "r".

C: To je definirana usmeritev, na kateri bo vektorska funkcija projicirana, dokler bo definirana za to ravnino.

F: Vektorska funkcija, kjer je vsaka njena komponenta opredeljena s funkcijo kot taka (F, G).

O: To je vektorska tangenta v regiji R, na katerem je definiran integral. V tem primeru deluje z diferenciacijo tega vektorja.

V drugem mandatu vidimo, da je Green razvil teorem, kjer opazimo dvojni integral, opredeljen v regiji r razlike v delnih derivatih G in F, glede na X oziroma. Za diferencial na območju, ki ni nič drugega kot produkt obeh dveh dimenzijskih razlik (DX.dy).

Ta teorem je popolnoma uporaben za vesoljske in površinske integrale.

Demonstracija

Če želite na preprost način pokazati Green -ov teorem, bo ta naloga razčlenjena na 2 dela. Najprej bomo domnevali, da ima vektorska funkcija samo definicijo v versoru Yo. Medtem ko funkcija "G", ki ustreza versoru J bo enak nič.

Vam lahko služi: koliko stotin se prilega desetini? (Primeri)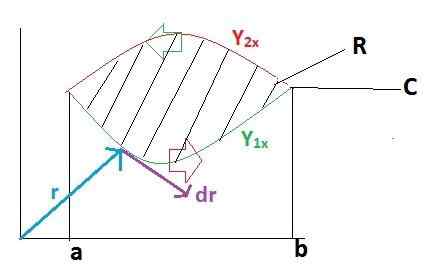Avtor

F = f (x, y)Yo + G (x, y)J = f (x, y)Yo + 0

R = xYo + inJ

Dr = dxYo + DyJ

Najprej razvijemo črto integral nad potjo C, za katero je bila usmeritev sektorizirana v dveh odsekih, ki gredo najprej od A do B in po B do A.

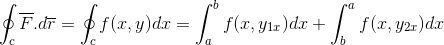
Uporablja se opredelitev temeljnega teorema izračuna za definiran integral.

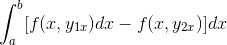
Izraz je preurejen v enem samem integralu, je skupno negativnemu in vrstni red faktorjev je obrnjen.

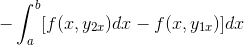
Z podrobnim opazovanjem tega izraza postane očitno, da je pri uporabi meril primitivne funkcije v prisotnosti integrala izraza, ki izhaja iz F glede na in. Ocenjeno v parametrih

[in_1x , in_2x]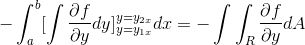

Zdaj je dovolj, da domnevamo, da je vektorska funkcija zabavna definirana samo za G (x, y)J. Kjer je deloval na način, ki je homologiran v prejšnji primer, dobimo:

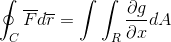
Končno se vzameta dve demonstraciji in se pridružita v primeru, ko vektorska funkcija prevzame vrednosti za oba verzorja. Na ta način je prikazan kot črta integral po definiranju in obravnavanem kot eno -dimenzionalni usmeritvi, ki ga je mogoče v celoti razviti za ravnino in prostor.

F = f (x, y)Yo + G (x, y)J

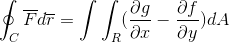
Na ta način je prikazan Green's Teorem.

Prijave

Uporaba zelenega teorema so široka v vejah fizike in matematike. Te segajo na katero koli aplikacijo ali uporabo, ki jo lahko damo integraciji linij.

Mehansko delo, ki ga opravlja sila F skozi pot C, lahko razvije linijski integral, ki je izražen kot dvojni integral območja skozi Green -ov izrek.

Vam lahko služi: petegonalna prizma: značilnosti, deli, točki, robovi, volumen

Inercijski trenutki številnih teles, ki so bili podvrženi zunanjim silam na različnih točkah uporabe, se odzivajo tudi na razvijajoče se integrale z Greenovim teoremom.

To ima več funkcionalnosti v študijah odpornosti materialov med uporabo. Kjer je mogoče zunanje vrednosti količinsko določiti in upoštevati pred izdelavo različnih elementov.

Na splošno Green -ov teorem olajša razumevanje in opredelitev območij, na katerih so vektorske funkcije opredeljene glede na regijo v skladu s potjo.

Zgodovina

Objavljeno je bilo leta 1828 v delu Matematična analiza teorij električne energije in magnetizma, napisal britanski matematik George Green. Raziskuje precej odločilne odseke pri uporabi izračuna v fiziki, kot so koncept potenciala, funkcije zelene in aplikacije njegovega avtoorema z naslovom.

George Green je svojo študentsko kariero formaliziral pri 40 letih, doslej popolnoma samought matematiko. Po študiju na univerzi v Cambridgeu se njegovo raziskovanje nadaljuje in prispeva na področju akustike, optike in hidrodinamike, ki še danes veljajo.

Odnos z drugimi teoremi

Green's Teorem je poseben primer in izhaja iz dveh drugih zelo pomembnih teoremov v veji za izračun. To so Kelvin-Stokesov teorem in teorem o razhajanju ali Gausskiju.

Začenši od katerega koli od obeh teoremov, lahko pridete do Green -ovega teorema. Za razvoj teh demonstracij so potrebne določene opredelitve in predloge.

Vaje

- Naslednja vaja prikazuje, kako spremeniti linijo integral v dvojni integral glede na regijo r.

Prvotni izraz je naslednji:

Vam lahko služi: koliko je vreden x?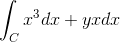

In ga je treba oceniti v trikotni regiji, ki se pridruži točkam (0, 0), (1, 0), (0, 1), označeno s C. V tem primeru bo upoštevan pozitiven občutek preobrata.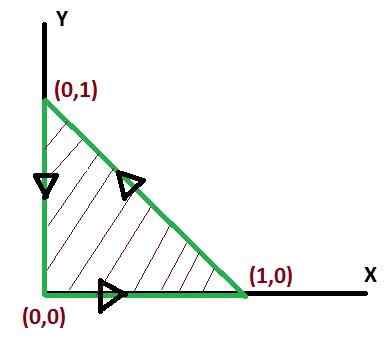

Od ko

f (x, y) = x³                      g (x, y) = yx

df/dy = 0 dg/dx = y

Pomembno je določiti funkcije, ki sestavljajo meje regije C, da lahko sestavite diferencialni izdelek, ki bo popolnoma zajel regijo.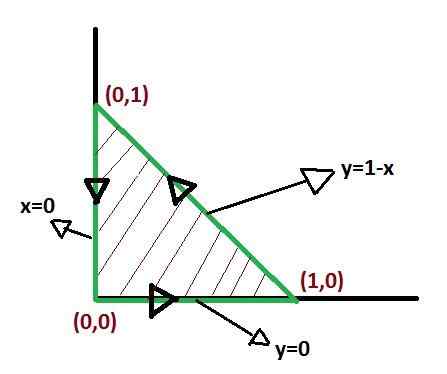

Pri uporabi Green -ovega teorema ni edinstvenega načina določanja omejitev integracije. Obstajajo pa obrazci, kjer so integrali po definiranju lahko enostavnejši. Na tak način, da si optimizacija omejitev integracije zasluži pozornost.

V tem primeru se šteje ta izraz: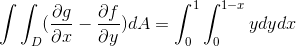

Kje pri reševanju integralov dobimo:

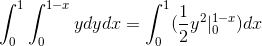
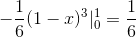
Ta vrednost v kubičnih enotah ustreza regiji pod vektorsko funkcijo in na trikotni regiji, ki jo določa c.

V primeru linije Integral brez izvajanja zelene metode bi bilo treba parametrizirati funkcije v vsakem odseku regije. To pomeni, da naredite 3 parametrizirane integrale za ločljivost. To je zadosten dokaz o učinkovitosti, ki jo je Robert Green prispeval s svojim izrek k izračunu.

Reference

1. Uvod v mehaniko Continum. W Michael Lai, David H. Rubin, Erhard Krempl, David Rubin Butterworth-Heinemann, 23. julij. 2009
2. Večvarni računanje. James Stewart. Cengage Learning, 22 marca. 2011
3. Neformalna zgodovina Green -ovega teorema in z njimi povezanih idej. James Joseph Cross. Oddelek za matematiko, Univerza v Melbournu, 1975
4. Toplotno vedenje z uporabo zelenja. Kevin d. Cole, James V. Beck, a. Haji-sheikh, Bahman Luckuhi. Taylor & Francis, 16. julij. 2010
5. Uporaba Green -ovega teorema za ekstremizacijo linearnih integralov. Obrambni informacijski informacijski center, 1961