Euclid teorem

Kaj je Euclidov teorem?

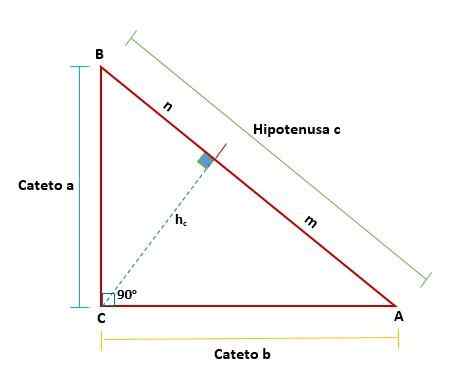
On Euclid teorem Prikazuje lastnosti desnega trikotnika, tako da nariše črto, ki jo razdeli na dva nova pravokotnika, ki sta podobna drug drugemu in sta posledično podobna prvotnemu trikotniku; Torej, obstaja razmerje sorazmernosti.

Euclides je bil eden največjih matematikov in geometrov starosti, ki so naredili več demonstracij pomembnih teoremov. Eden glavnih je tisti, ki nosi njegovo ime, ki je imel široko uporabo.

To je bilo tako, ker s tem teoremom geometrijske odnose, ki obstajajo v pravokotniku Trikotnik, pojasnjuje, kje so to povezane z njihovimi projekcijami v hipotenuzi.

Formule in demonstracije

Euclid teorem predlaga, da v vsakem desnem trikotniku, ko je narisana črta - kar predstavlja na višini, ki ustreza vrhovi desnega kota glede na hipotenuzo - iz originalnih trikotnikov iz originala tvorita dva pravokotnika.

Ti trikotniki bodo podobni drug drugemu in bodo podobni tudi prvotnemu trikotniku, kar pomeni, da so njihove podobne strani sorazmerne med seboj:

Koti treh trikotnikov so skladni; To pomeni, da ko se vrti na 180 stopinj na vrhu, kot na drugi sovpada kot. To pomeni, da bodo vsi enaki.

Na ta način lahko preverite tudi podobnost, ki obstaja med tremi trikotniki, za enakost njegovih kotov. Od podobnosti trikotnikov Euclid določa delež teh iz dveh teoremov:

• Teorem o višini.
• Izrek Catetosa.

Ta teorem ima široko aplikacijo. V starih časih je bil uporabljen za izračun višin ali razdalj, kar predstavlja velik napredek za trigonometrijo.

Vam lahko služi: izračun pristopov z uporabo diferencialov

Trenutno se uporablja na različnih področjih, ki temeljijo na matematiki, kot so inženiring, fizika, kemija in astronomija, med drugimi območji.

Teorem o višini

Ta teorem ugotovi, da je v katerem koli pravokotniškem trikotniku višina, ki je bila narisana iz pravega kota glede na hipotenuzo.

To pomeni, da bo kvadrat višine enak množenju projiciranih nog, ki tvorijo hipotenuzo:

h_c² = m _* n

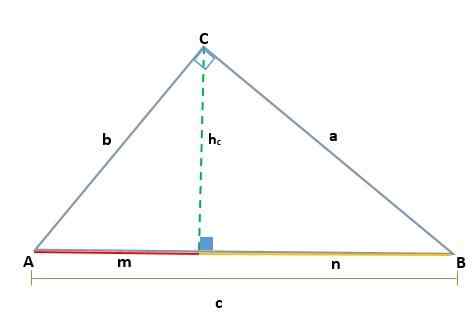
Demonstracija

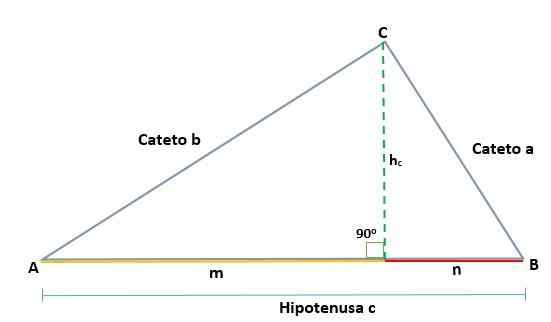
Glede na ABC trikotnik, ki je pravokotnik v Vertex C, se ustvarita dva podobna pravokotnika, ADC in BCD; Zato so njihove ustrezne strani sorazmerne:

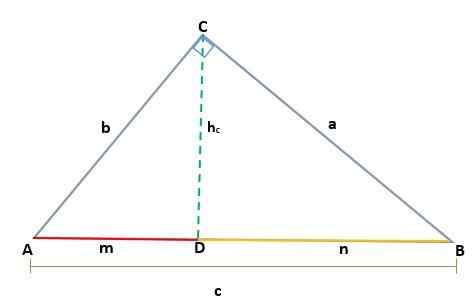
Na tak način, kot je višina h_c Ustreza segmentu CD -ja, ustreza hipotenuzi AB = C, zato morate:

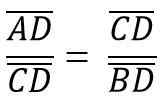
To pa ustreza:

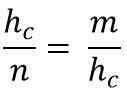
Čiščenje hipotenuze (h_c), Za pomnožitev obeh članov enakosti morate:

h_{C *} h_{C =} m _* n

h_c² = m _* n

Tako je vrednost hipotenuze podana z:

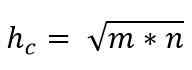
Izrek Catetosa

Ta teorem ugotovi, da bo v vsakem desnem trikotniku ukrep vsakega kateta geometrijsko proporcionalno povprečje (kvadrat vsakega cateto) med mero hipotenuze (celotno) in projekcijo vsake na njem:

b² = c _* m

do² = c_* n

Demonstracija

Glede na ABC trikotnik, ki je pravokotnik v Vertex C, tako da je njegova hipotenuza c, pri risanju višine (h) so določene projekcije kategorij A in B, ki sta segmenta M in N Hipotenuza.

Tako višina, narisana na trikotniku pravokotnika ABC, ustvari dva podobna pravokotnika, ADC in BCD, tako da so ustrezne strani sorazmerne, kot je ta:

Vam lahko služi: hiperbolični paraboloid: definicija, lastnosti in primeri

Db = n, kar je projekcija CB cateto na hipotenuzi.

Ad = m, kar je projekcija AC Cateto na hipotenuzi.

Nato je hipotenza C določena z vsoto nog njegovih projekcij:

C = M + N

Zaradi podobnosti trikotnikov ADC in BCD morate:

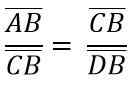
Zgoraj je enako kot:

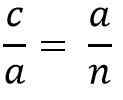
Če želite očistiti "A", da pomnožimo dva člana enakosti, morate:

do _* a = c _* n

do² = c _* n

Tako je vrednost Cateto "A" podana z:

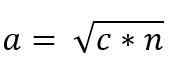
Podobno morate zaradi podobnosti trikotnikov ACB in ADC:

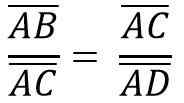
Zgoraj je enako:

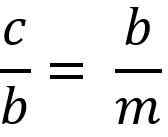
Če želite čistiti "B" kateto Za pomnožitev obeh članov enakosti, morate:

b _* b = c _* m

b² = c _* m

Tako je vrednost Cateto "B" podana z:

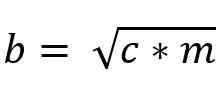
Razmerje med teoremi Euclid

Teoremi glede na višino in kategorije so med seboj povezani, ker se merilo obeh izvaja glede na hipotenuzo pravokotnika trikotnika.

Skozi razmerje med teoremi Euclid je mogoče najti tudi vrednost višine; To je mogoče z odstranjevanjem vrednosti m in n teorema kategorije in se nadomestijo v teoremu. Na ta način se izpolnjuje, da je višina enaka množenju nog, razdeljena s hipotenuzo:

b² = c _* m

M = b² ÷ c

do² = c _* n

n = a² ÷ c

V višini je teorem M in N zamenjan:

h_c² = m _* n

h_c² = (b² ÷ c) _* (do² ÷ c)

h_c = (b² _* do²) ÷ c

Rešene vaje

Primer 1

Glede na trikotnik ABC, pravokotnik v a, določite mero AC in AD, če AB = 30 cm in BD = 18 cm

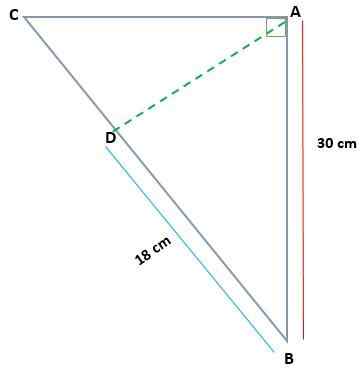
Rešitev

V tem primeru obstajajo ukrepi ene od načrtovanih nog (BD) in enega od tark prvotnega trikotnika (AB). Tako lahko uporabite teorem kategorije in poiščete vrednost BC Cateto.

Vam lahko služi: pravilo dopisovanja funkcije

Ab² = Bd _* Pr

(30)² = 18 _* Pr

900 = 18 _* Pr

BC = 900 ÷ 18

BC = 50 cm

Vrednost CD Cateto je mogoče najti, vedoč, da je BC = 50:

CD = BC - BD

CD = 50 - 18 = 32 cm

Zdaj je mogoče določiti vrednost AC Cateto in ponovno uporabiti teorem kategorije:

AC² = CD _* Bd

AC² = 32 _* petdeset

AC² = 160

AC = √1600 = 40 cm

Za določitev vrednosti višine (AD) velja teorem o višini, saj sta vrednosti načrtovanih kategorij CD in BD znani:

Oglas² = 32 _* 18

Oglas² = 576

AD = √576

AD = 24 cm

Primer 2

Določite vrednost višine (h) MNL trikotnika, pravokotnik v N, pri čemer poznate ukrepe segmentov:

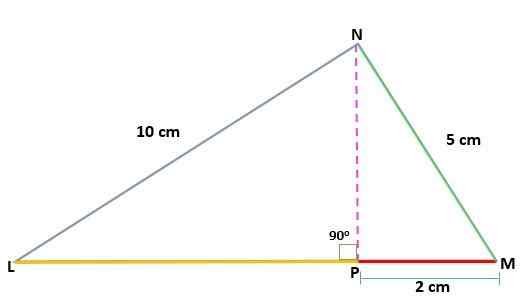
Nl = 10 cm

Mn = 5 cm

Pm = 2 cm

Rešitev

Na hipotenuzi (PM) imate merilo ene od načrtovanih nog, pa tudi ukrepe prvotnih kategorij trikotnika. Tako lahko uporabite teorem kategorije in poiščete vrednost drugega projiciranega Cateto (LN):

Nl² = Pm _* Lm

(10)² = 5 _* Lm

100 = 5 _* Lm

Pl = 100 ÷ 5 = 20

Ker je vrednost kategorij in hipotenuze že znana, je mogoče skozi razmerje med teoremi višine in kategorije določiti vrednost višine:

Nl = 10

Mn = 5

Lm = 20

H = (b² _* do²) ÷ c.

H = (10² _* 5²)  ÷ (dvajset)

H = (100 _* 25) ÷ (dvajset)

H = 2500 ÷ dvajset

H = 125 cm.