Chebyshov teorem, to je aplikacije in primeri

On Chebyshov teorem (ali neenakost Chebyshova) je eden najpomembnejših klasičnih rezultatov teorije verjetnosti. Omogoča oceno verjetnosti dogodka, opisanega v smislu naključne spremenljivke X, tako da nam zagotavlja raven, ki ni odvisna od porazdelitve naključne spremenljivke, ampak od variance x.

Teorem se imenuje v čast ruske matematike.

Ta neenakost ali tiste, ki se zaradi njihovih značilnosti imenujejo neenakost Chebyshova, se uporablja predvsem za približevanje verjetnosti s pomočjo izračuna ravni.

Kaj je Chebyshov teorem?

V preučitvi teorije verjetnosti se zgodi, da če je znana porazdelitev funkcije naključne spremenljivke x zneske obstajajo. Vendar vzajemna ni nujno resnična.

To pomeni, da poznavanje E (x) in var (x) ne more nujno pridobiti porazdelitvene funkcije x, zato je količin, kot je p (| x |> k), za nekatere k> 0 zelo težko dobiti. Toda zahvaljujoč Chebyshovi neenakosti je mogoče oceniti verjetnost naključne spremenljivke.

Chebyshov teorem nam pove, da če imamo naključno spremenljivko x na vzorčnem prostoru s funkcijo verjetnosti p, in če je k> 0, potem:

Vam lahko služi: akutantni trikotnik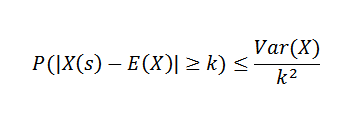

Aplikacije in primeri

Med številnimi aplikacijami, ki jih ima Chebyshov teorem, je mogoče omeniti naslednje:

1. Mejna verjetnost

To je najpogostejša aplikacija in se uporablja za dajanje zgornje ravni za p (| x-e (x) | ≥K), kjer je k> 0, le z varianco in upanjem naključne spremenljivke x, ne da bi vedel funkcijo verjetnosti.

Primer 1

Recimo, da je število izdelkov, izdelanih v podjetju za en teden, naključna spremenljivka s povprečjem 50.

Če je znano, da je odstopanje v tednu proizvodnje enaka 25, kaj lahko rečemo o verjetnosti, da se ta teden proizvodnja razlikuje za več kot 10 do povprečja?

Rešitev

Če uporabimo Chebyshovo neenakost, moramo:

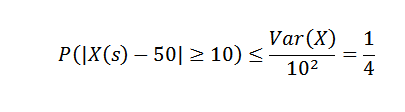
Iz tega lahko ugotovimo, da je verjetnost, da v tednu proizvodnje število postavk presega več kot 10 do povprečja, največ 1/4.

2. Demonstracija mejnih teoremov

Chebyshova neenakost ima pomembno vlogo pri prikazu najpomembnejših teoremov o omejitvah. Kot primer imamo naslednje:

Šibek zakon velikega števila

Ta zakon določa, da je dal nasledstvo x1, x2, ..., xn, ... neodvisnih naključnih spremenljivk z enako povprečno porazdelitev e (xi) = μ in variance var (x) = σ², in znani povprečni vzorec:

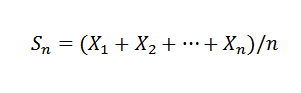
Torej za k> 0 moraš:

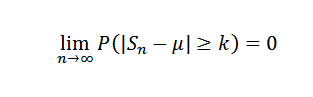
Ali enakovredno:

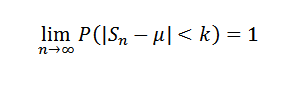
Demonstracija

Najprej opazimo naslednje:

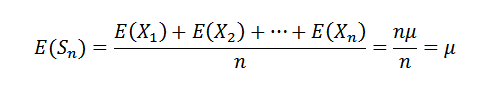
Ker so x1, x2, ..., xn neodvisni, sledi:

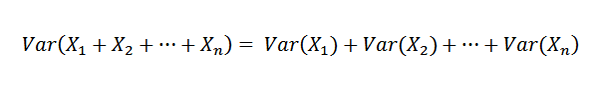
Zato je mogoče potrditi naslednje:

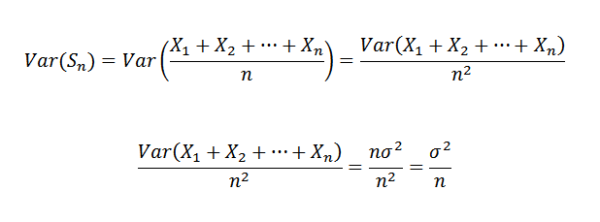
Nato morate s Chebyshovim izrek:

Lahko vam služi: trigonometrične funkcije: Osnovne, v kartezijanski ravnini, primeri, vadba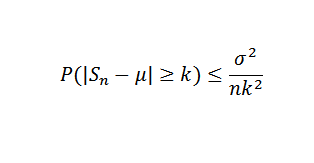

Končno je izrek posledica dejstva, da je desna meja enaka, ko se N nagiba k neskončnosti.

Treba je opozoriti, da je bil ta test opravljen samo za primer, v katerem je odstopanje XI; Se pravi, da se ne razlikuje. Tako opažamo, da je teorem vedno resničen, če obstaja E (xi).

Chebyshov mejni teorem

Če x1, x2, ..., xn, ... je nasledstvo neodvisnih naključnih spremenljivk, tako da obstaja nekaj C0:

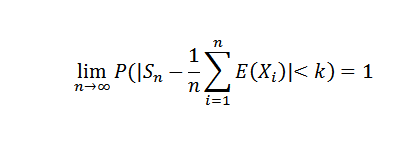
Demonstracija

Ker je nasledstvo odstopanj enakomerno omejeno, imamo ta var (sn) ≤ c/n, za vse naravne n. Ampak to vemo:

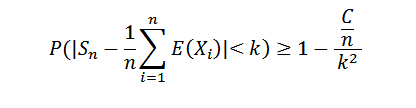
Naredi n do neskončnosti, je naslednje:

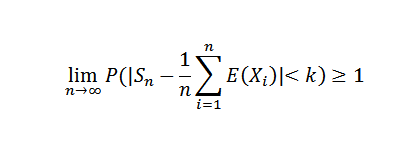
Ker verjetnost ne more preseči vrednosti 1, se dobi želeni rezultat. Zaradi tega izrek lahko omenimo poseben primer Bernoullija.

Če se poskus ponovi neodvisno z dvema možnima rezultatima (neuspeh in uspehom), kjer je P verjetnost uspeha v vsakem poskusu in X je naključna spremenljivka, ki predstavlja število pridobljenih uspehov, potem morate za vsako k> 0:

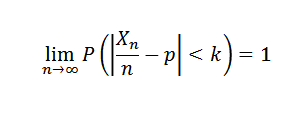
3. Velikost vzorca

Glede na odstopanje nam neenakost Chebyshova omogoča, da najdemo velikost vzorca, ki zadostuje za zagotovitev, da je verjetnost, da se pojavi | sn-μ |> = K povprečje.

Natančno, naj bo to x1, x2, ... xn Vzorec neodvisnih naključnih spremenljivk velikosti n in predpostavimo, da je E (xi) = μ in njegova varianta σ². Torej, zaradi neenakosti Chebyshova morate:

Vam lahko služi: Eulerjeva številka ali številka E: koliko v redu, lastnosti, aplikacije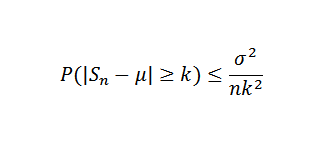

Zdaj naj bo Δ> 0 popravljen. Moramo:

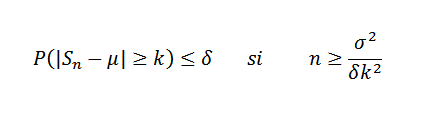
Primer

Recimo, da so x1, x2, ... xn vzorec neodvisnih naključnih spremenljivk z Bernoullijevo porazdelitvijo, tako da vzamejo vrednost 1 z verjetnostjo p = 0.5.

Kakšna bi morala biti velikost vzorca, da se zagotovi, da je verjetnost, da je razlika med aritmetično srednjo vrednostjo in njegovo pričakovano vrednostjo (ki presega več kot 0,1), manjša ali enaka 0.,01?

Rešitev

Moramo (x) = μ = p = 0,5 in kaj var (x) = σ²= P (1-p) = 0,25. Za neenakost Chebyshova moramo za katero koli k> 0:

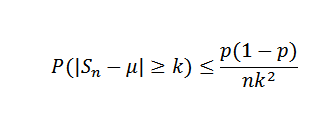
Zdaj jemljete k = 0,1 in Δ = 0,01, morate:

Na ta način je ugotovljeno, da je potrebna velikost vzorca vsaj 2500, da se zagotovi, da je verjetnost dogodka | Sn - 0,5 |> = 0,1 manjša od 0,01.

Neenakosti tipa Chebyshov

Obstajajo različne neenakosti, povezane z neenakostjo Chebyshova. Ena najbolj znanih je Markova neenakost:

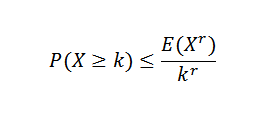
V tem izrazu x je ne -negativna naključna spremenljivka s k, r> 0.

Markova neenakost lahko ima različne oblike. Na primer bodisi in negativna naključna spremenljivka (torej p (y> = 0) = 1) in predpostavimo, da E (y) = μ obstaja. Predpostavimo tudi, da (e (y))^r= μ_r Obstaja za nekaj celoštevilčnega r> 1. Tako:

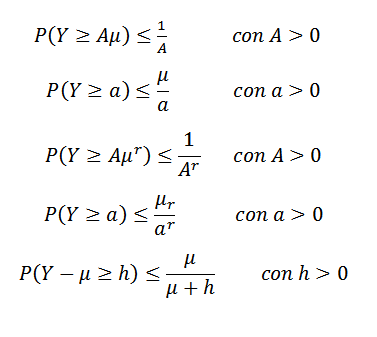
Druga neenakost je Gauss, ki nam pove, da je dala enomidalno x naključno spremenljivko z modo na nič, nato za K> 0,