Teorija značilnosti naborov, elementov, primeri, vaje

The teorija nastavitve To je veja logične matematike, ki je odgovorna za preučevanje odnosov med subjekti, imenovanimi nabori. Za sklope so značilne zbirke predmetov iste narave. Ti predmeti so elementi nabora in so lahko: številke, črke, geometrijske figure, besede, ki predstavljajo predmete, predmete in druge.

Konec 19. stoletja je bil Georg Cantor, ki je predlagal niz sklopov. Medtem ko so drugi pomembni matematiki v dvajsetem stoletju naredili formalizacijo: Gottlob Frege, Ernst Zermelo, Bertrand Russell, Adolf Fraenkel.

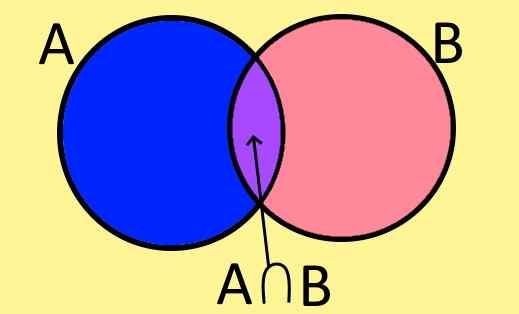
Slika 1. Vennov diagram sklopov A, B in njihovega križišča A⋂ B. (Lastna izdelava).

Vennovi diagrami so grafični način predstavljanja niza in je sestavljen iz zaprte ravne figure, znotraj katere so elementi kompleta.

Na primer, na sliki 1 prikazujeta dva sklopa A in B, ki imata skupne elemente, elemente, ki so skupni A in B. Ti tvorijo nov komplet, imenovan križišče A in B, ki je napisan simbolično na naslednji način:

A ∩ B

[TOC]

Značilnosti

Set je primitiven koncept, saj je v geometriji koncept točke, ravne ali ravne. Ni boljšega načina za izražanje koncepta, kot da bi opozorili na primere: 

Komplet in oblikovan z barvami zastavice Španije. Ta način izražanja nabora se imenuje z razumevanjem. Isti niz in zapisan po podaljšanju je:

E = rdeča, rumena

V tem primeru sta rdeča in rumena elementi kompleta in. Treba je opozoriti, da so elementi navedeni med tipkami in se ne ponavljajo. V primeru španske zastave so tri črte barv (rdeča, rumena, rdeča), od katerih se dva ponovita, vendar se elementi ne ponavljajo, ko je nabor izražen.

Predpostavimo, da je nastavljen v prvih treh vokalnih črk:

V = a, e, i

Moč V, ki jo označuje P (v), je niz vseh sklopov, ki jih je mogoče oblikovati z elementi V:

P (v) = a, e, i, a, e, a, i, e, i, a, e, i

Vrste sklopov

Končni komplet

Je komplet, v katerem so njegovi elementi številni. Primeri končnih nizov so črke španske abecede, samoglasniki španščine, planetov sončnega sistema. Število elementov končnega niza se imenuje njegova kardinalnost.

Neskončni komplet

Neskončni ansambel, vsi, ki števila njegovih elementov niso nesporni, saj ne glede na to, kako veliko je število njegovih elementov, je vedno mogoče najti več elementov.

Neskončni primer je nabor naravnih števil N, ki je obsežno izražen na naslednji način:

Vam lahko služi: Coplanares Točke: enačba, primer in rešene vaje

N = 1, 2, 3, 4, 5, .. . je očitno neskončen nabor, saj ni pomembno, kako veliko je lahko naravno število, naslednje lahko v neskončnem postopku vedno najde. Očitno je kardinalnost neskončnega niza ∞.

Prazen komplet

Je niz, ki ne vsebuje nobenega elementa. Prazen komplet V označuje Ø ali s parom tipk brez elementov v notranjosti:

V = = Ø.

Prazen niz je edinstven, zato mora biti napačno reči "prazen niz", pravilen obrazec pa je reči "prazen niz".

Med lastnostmi praznega niza je, da gre za podskupino katerega koli nabora:

Ø ⊂ a

Poleg tega, če je niz podskupine praznega niza, bo ta niz nujno praznina:

A ⊂ Ø ⇔ a = Ø

Enotni komplet

Imenuje se enoten niz poljubnega niza, ki vsebuje en sam element. Na primer, nabor naravnih satelitov Zemlje je enota, katerega edini element je luna. Nastavitev B celih števil, manjših od 2 in večje od nič, ima samo element 1, zato je enota.

Binarni komplet

Set je binarni, če ima samo dva elementa. Na primer nastavite x, tako da je x resnično število x^2 = 2 = 2. Ta komplet po razširitvi je napisan tako:

X = -√2, +√2

Univerzalni komplet

Univerzalni niz je komplet, ki vsebuje druge sklope iste vrste ali narave. Na primer, univerzalni niz naravnih števil je nabor resničnih številk. Toda realne številke so tudi univerzalne celotne številke in racionalne številke.

Temeljni elementi

- Odnosi med sklopi

V sklopih lahko vzpostavite več vrst odnosov med njimi in njihovimi elementi. Če imata dva sklopa A in B popolnoma enake elemente, je med njimi enakovredno razmerje označeno na naslednji način:

Do = B

Če vsi elementi niza, ki pripadajo kompletu B, vendar ne vsi elementi B pripadajo A, potem je med temi nabornimi razmerja, ki je označen na naslednji način:

A ⊂ b, vendar b ⊄ a

Prejšnji izraz se glasi: A je podskupina B, vendar B ni podskupina a.

Če navedemo, da nekateri ali nekateri elementi pripadajo nizu, se uporablja simbol pripadnosti ∈, na primer, da rečemo, da je X element ali elementi na niz A napisan simbolično na naslednji način:

x ∈ A

Da Element in ne pripada temu, da je ta odnos napisan tako:

in ∉ a

Pripadno razmerje je podano med elementi niza in niz, z edino izjemo moči, ki je zbirka ali niz vseh možnih sklopov, ki jih je mogoče oblikovati z elementi omenjenega seta.

Vam lahko služi: faktorizacija

Predpostavimo v = a, e, i, tvoja moč je p (v) = a, e, i, a, e, a, i, e, i, a, e, i, v tem primeru nabor V postane element nabora p (v) in ga je mogoče zapisati:

V ∈ P (v)

- Lastnosti vključitve

Prva lastnost vključenosti določa, da je vsak sklop vsebovan sam po sebi ali z drugimi besedami, ki je podvrsta samega sebe:

A ⊂ a

Druga lastnost vključitve je tranzitivnost: če je A podvrsta B in B po vrsti, je podskupina C, potem je A podskupina C. Simbolično je odnos tranzitivnosti napisano tako:

(A ⊂ b) ^ (b ⊂ c) => a ⊂ c

Spodaj je Vennov diagram, ki ustreza tranzitivnosti vključenosti:

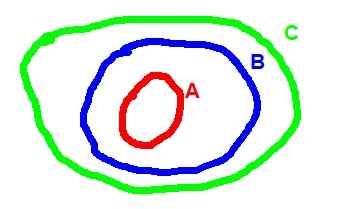Slika 2. (A ⊂ b) ^ (b ⊂ c) => a ⊂ c

- Operacije med nizi

Križišče

Križišče je operacija med dvema nizoma, ki ima za posledico nov niz, ki pripada istemu univerzalnemu nizu prvih dveh. V tem smislu je zaprta operacija.

Simbolično je operacija križišča oblikovana na naslednji način:

A⋂b = x / x∈A ^ x∈B

Primer je naslednji: nastavite črke A v besedi "elementi" in nastavite B črk besede "ponavljajoče se", križišče med A in B je napisano tako:

A⋂b = e, l, m, n, t, s ⋂ r, e, p, t, i, d, o, s = e, t, s . Univerzalni sklop A, B in tudi A⋂B je nabor črk španske abecede.

Zvezo

Zveza dveh nizov je niz, ki ga tvorijo elementi, ki so skupni obema nizoma, in nemočani elementi obeh nizov. Operacija Unije med nizi je izražena simbolično na naslednji način:

A∪b = x/x∈A v x∈B

Razlika

Delovanje vsaj niza je označeno z A-B. A-B je nov komplet, ki ga tvorijo vsi elementi, ki so v A in ki ne pripadajo B. Simbol je napisan takole:

A - b = x/ x ∈ A ^ x ∉ b

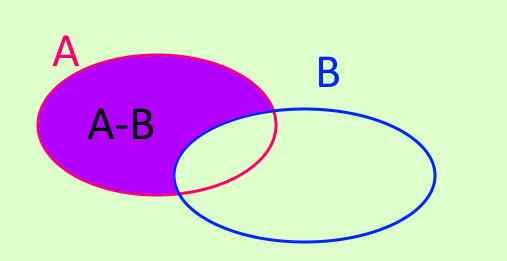Slika 3. A - b = x/ x ∈ A ^ x ∉ b

Simetrična razlika

Simetrična razlika je operacija med dvema nizoma, kjer je nastali niz sestavljen iz elementov, ki niso skupni obema nizoma. Simetrična razlika simbolično je predstavljena na naslednji način:

A⊕b = x/ x∈ (a-b) ^ x∈ (b-a)

Primeri

Primer 1

Vennov diagram je grafični način za predstavljanje nizov. Na primer, nastavite C črk nabora besed je predstavljeno na naslednji način:

Primer 2

Spodaj je prikazan skozi Vennove diagrame, da je niz samoglasnikov v besedi "nastavi" podskupina nabora črk besede "nastavitev".

Vam lahko služi: vzorčenje kvot: metoda, prednosti, slabosti, primeri

Primer 3

Set Ñ Iz črk španske abecede je končni niz, ta komplet po razširitvi je napisan tako:

Ñ = A, B, C, D, E, F, G, H, I, J, K, L, M, N, ñ, O, P, Q, R, S, T, U, V, V, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, X, Y, Z in ITS Kardinalnost je 27.

Primer 4

Set V Od samoglasnikov v španščini je podskupina kompleta:

V ⊂ Ñ Zato je končni komplet.

Končni komplet V Iztegnjen način je napisan tako: V = a, e, i, o, u in njegova kardinalnost je 5.

Primer 5

Glede na sklope A = 2, 4, 6, 8 in B = 1, 2, 4, 7, 9 Določite A-B in B-A. 

A - B so elementi, ki jih niso v B:

A - b = 6, 8

B - A so elementi B, ki niso v A:

B - a = 1, 7, 9

Rešene vaje

Vaja 1

Simbolično napišite in tudi s podaljšanjem cvetnega lita naravnega števila celo nižji od 10.

Rešitev: P = x∈ N / x < 10 ^ x mod 2 = 0

P = 2, 4, 6, 8

Vaja 2

Predpostavimo, da je celota, ki jo tvorijo naravne številke, ki so dejavniki 210. Določite oba sklopa po razširitvi in ​​ugotovite, kakšen odnos je med obema sklopoma.

Rešitev: Če želite določiti elemente nastavitve A, morate začeti z iskanjem dejavnikov naravne številke 210:

210 = 2 * 3 * 5 * 7

Nato je napisan napisan:

A = 2, 3, 5, 7

Nadaljujemo s set B, ki je bratranci, manjši od 9. 1 ni bratranec, ker ne ustreza definiciji bratranca: "Številka je bratranec, če in samo, če ima natanko dva delitve 1 in samo številko". 2 je enakomerna in hkrati je bratranec, ker izpolnjuje definicijo bratranca, ostali bratranci, manjši od 9, so 3, 5 in 7. Torej je ta komplet B:

B = 2, 3, 5, 7

Zato sta oba sklopa enaka: a = B.

Vaja 3

Določite niz, katerega elementi x so različni od x.

Rešitev: C = x / x ≠ x

Kot kateri koli element je tudi število ali objekt enak samemu sebi, tudi set c ne more biti drug kot prazen niz:

C = Ø

Vaja 4

Biti niz n naravnih števil in z nabor celih številk. Določite n ⋂ z y n ∪ z.

Rešitev: 

N ⋂ z = x ∈ Z / x ≤ 0 = (-obžaločen, 0]

N ∪ z = z, ker n ⊂ z.

Reference

1. Garo, m. (2014). Matematika: kvadratne enačbe: Kako reševanje kvadratne enačbe. Marilù Garo.
2. Haeussler, npr. F., & Paul, r. S. (2003). Matematika za upravo in ekonomijo. Pearson Education.
3. Jiménez, J., Rodríguez, m., Estrada, r. (2005). Matematika 1 sep. Prag.
4. Dragoceno, c. T. (2005). Tečaj matematike 3o. Uredništvo Progreso.
5. Matematika 10 (2018). "Primeri končnih nizov". Pridobljeno iz: matematika10.mreža
6. Wikipedija. Teorija nastavitve. Okrevano od: je.Wikipedija.com