Primeri, pravila in vaje za kvadratne nasledstva

The Kvadratne nasledstva, V matematičnem smislu so sestavljene iz zaporedja števil, ki sledijo določenemu aritmetičnemu pravilu. Zanimivo je vedeti to pravilo, da določite kateri koli od pogojev nasledstva.

Eden od načinov za to je določiti razliko med dvema zaporednima izrazi in preveriti, ali se dobiva vrednost vedno ponovi. Ko je tako, se reče, da je redno nasledstvo.

Numerične naslednje so način organiziranja zaporedja številk. Vir: Pixabay.com

Če pa se ne ponovi, potem lahko poskusite preučiti razlika med razlikami In poglejte, ali je ta vrednost konstantna. Če je tako, potem je Kvadratno nasledstvo. 

[TOC]

Primeri rednih in kvadratnih nasledstva

Naslednji primeri pomagajo razjasniti, kaj je bilo do zdaj razloženo:

Primer rednega nasledstva

Biti nasledstvo s = 4, 7, 10, 13, 16, ...

Ta nasledstvo, ki ga označuje S, je neskončen številčni niz, v tem primeru celotnih številk.

Vidimo, da gre za redno nasledstvo, saj se vsak izraz dobi z dodajanjem 3 k prejšnji izraz ali element:

4

4 +3 = 7

7+3 = 10

10+3 = 13

13+3 = 16

Z drugimi besedami: to nasledstvo je redno, ker razlika med naslednjim izrazom in prejšnjim daje fiksno vrednost. V primeru, če je ta vrednost 3.

Prav tako se imenujejo tudi redni nasledji, pridobljeni z dodajanjem fiksnega zneska, imenovani se Aritmetični napredek. In na razliko - konstantno - med zaporednimi izrazi se imenuje razlog In označena je kot r.

Primer neregularnega in kvadratnega nasledstva

Glej zdaj naslednje nasledstvo:

S = 2, 6, 12, 20, 30, .. .

Ko se izračunajo zaporedne razlike, dobimo naslednje vrednosti:

Vam lahko služi: naključne izbire z ali brez zamenjave

6-2 = 4

12-6 = 6

20-12 = 8

30-20 = 10

Njihove razlike niso stalne, zato lahko rečemo, da gre za neregularno nasledstvo.

Če pa upoštevamo nabor razlik, obstaja še eno nasledstvo, ki bo označeno kot S_Razlika:

S_Razlika = 4, 6, 8, 10, .. .

To novo nasledstvo je redno nasledstvo, Ker se vsak izraz dobi z dodajanjem fiksne vrednosti r = 2 v prejšnjo. Zato lahko trdimo, da je S Kvadratno nasledstvo.

Splošno pravilo za gradnjo kvadratnega nasledstva

Obstaja splošna formula za gradnjo kvadratnega nasledstva:

T_n = A ∙ n² + B ∙ n +c

V tej formuli, t_n To je izraz N nasledstva. A, B in C so fiksne vrednosti, medtem ko se N spreminjajo ena za drugo, to je 1, 2, 3, 4, ..

V nasledstvu s prejšnjega primera a = 1, b = 1 in c = 0. Od tam sledi, da je formula, ki ustvarja vse izraze,: t_n = n² + n

To pomeni:

T₁ = 1² + 1 = 2

T₂ = 2² + 2 = 6

T₃ = 3² + 3 = 12

T₅ = 5² + 5 = 30

T_n = n² + n

Razlika med dvema zaporednima pogojev kvadratnega nasledstva

T_N+1 - T_n = [A ∙ (n+1)² + B ∙ (n + 1) + c] - [a ∙ n² + B ∙ n +c]

Razvoj izraza skozi izjemni izdelek ostaja:

T_N+1 - T_n = A ∙ n² + A ∙ 2 ∙ n + a + b ∙ n + b + c - a ∙ n² - B ∙ n - c

S poenostavitvijo, ki ga dobite:

T_N+1 - T_n = 2 ∙ a ∙ n + a + b

To je formula, ki daje nasledstvo razlik_Razlika ki je mogoče napisati tako:

Razlika_n = A ∙ (2n+1)+b

Kjer je očitno naslednji izraz 2 ∙ včasih prejšnji. To je razlog za nasledstvo razlik_Razlika Es: r = 2 ∙ a.

Rešene vaje kvadratnih nasledstva

Vaja 1

Biti nasledstvo s = 1, 3, 7, 13, 21,…. Določite da:

i) To je redno ali ne

ii) je kvadratna ali ne

iii) je bil kvadraten, nasledstvo razlik in njihov razum

Lahko vam služi: omejitve lastnosti (s primeri)

Odgovori

i) Izračunamo razliko naslednji izraz in prejšnji:

3-1 = 2

7-3 = 4

13-7 = 6

21-13 = 8

Lahko trdimo, da nasledstvo ni redno, saj razlika med zaporednimi izrazi ni konstantna.

ii) nasledstvo razlik je redno, saj je razlika med njegovimi izrazi konstantna vrednost 2. Zato je prvotno nasledstvo s kvadratno.

iii) Že smo ugotovili, da je S kvadraten, nasledstvo razlik je:

S_Razlika = 2, 4, 6, 8,… in njegov razlog je r = 2.

Vaja 2

Biti nasledstvo s = 1, 3, 7, 13, 21,… prejšnjega primera, kjer je bilo preverjeno, da je kvadratna. Določiti:

i) formula, ki določa splošni izraz t_{n .}

ii) Preverite tretji in peti mandat.

iii) vrednost desetega mandata.

Odgovori

i) Splošna formula t_n je ∙ n² + B ∙ n +c. Potem je znano vrednosti a, b in c.

Nasledstvo razlik je pravilno 2. Poleg kakršnega koli kvadratnega nasledstva je razlog, da je R 2 ∙ A, kot je prikazano v prejšnjih razdelkih.

R = 2 ∙ a = 2, kar nas vodi do sklepanja, da je a = 1.

Prvi izraz nasledstva razlik_Razlika Je 2 in mora izpolnjevati ∙ (2n+1)+b, z n = 1 in a = 1, to je:

2 = 1 ∙ (2 ∙ 1+1)+B

Čiščenje B je dobimo: B = -1

Potem prvi izraz S (n = 1) vale 1, torej: 1 = a ∙ 1² + B ∙ 1 + c. Kot že vemo, da sta a = 1 in b = -1, ki nas nadomešča, ostanemo:

1 = 1 ∙ 1² + (-1) ∙ 1 +c

Čiščenje C dobiva vrednost: C = 1.

V povzetku:

A = 1, b = -1 in c = 1

Potem je izraz pravičen_n = n² - N + 1

ii) tretji izraz t₃ = 3² - 3 + 1 = 7 in je preverjeno. Peti t₅ = 5² - 5 + 1 = 21, kar je tudi preverjeno.

iii) deseti izraz bo t₁₀ = 10² - 10 + 1 = 91.

Vaja 3

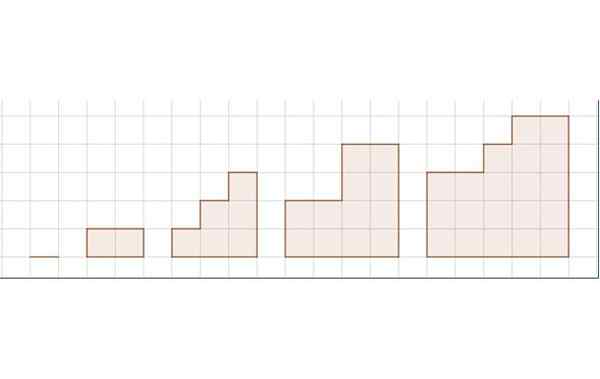Zaporedje območij za vajo 3. Vir: Self Made.

Slika prikazuje zaporedje petih številk. Retikulat predstavlja enoto dolžine.

Vam lahko služi: razlika med skupno frakcijo in decimalno številko

i) Določite nasledstvo za območje številk.

i) pokazati, da gre za kvadratno nasledstvo.

iii) Poiščite območje slike # 10 (ni prikazano).

Odgovori

i) nasledstvo, ki ustreza območju zaporedja figur, je:

S = 0, 2, 6, 12, 20,…

ii) nasledstvo, ki ustreza zaporednim razlikam v pogojih S, je:

S_Razlika = 2, 4, 6, 8,…

Ker razlike med zaporednimi izrazi niso konstantne, zato S ni redno nasledstvo. Vedeti mora, ali je kvadratna, za kar spet naredimo zaporedje razlik, pridobimo:

2, 2, 2, .. .

Ker se vsi pogoji zaporedja ponovijo, je potrjeno, da je S kvadratno nasledstvo.

iii) nasledstvo s_Razlika je reden in njen razlog r je 2. Z uporabo prej prikazane enačbe r = 2 ∙ a ostaja:

2 = 2 ∙ a, kar pomeni, da je a = 1.

Drugi izraz nasledstva razlik_Razlika Je 4 in N-EME S_Razlika je

A ∙ (2n+1)+b.

Drugi izraz ima n = 2. Ugotovljeno je bilo tudi, da je A = 1, zato je uporaba prejšnje enačbe in zamenjava:

4 = 1 ∙ (2 ∙ 2+1)+B

Čiščenje B je dobimo: B = -1.

Znano je, da je drugi izraz S vreden 2 in da se mora formula splošnega izraza izpolniti z n = 2:

T_n = A ∙ n² + B ∙ n +c; n = 2; A = 1; B = -1; T₂ = 2

To pomeni

2 = 1 ∙ 2² - 1 ∙ 2 + c

Ugotovljeno je, da je C = 0, to pomeni, da je formula, ki daje splošni izraz nasledstva S:

T_n = 1 ∙ n² - 1 ∙ n +0 = n² - n

Zdaj je preverjen peti mandat:

T₅ = 5² - 5 = 20

iii) Slika št. 10, ki tukaj ni bila narisana, bo območje, ki ustreza desetem mandatu nasledstva:

T₁₀ = 10² - 10 = 90

Reference

1. https: // www.Geogebra.org