Sestavno nasledstvo

Nasledstvo, sestavljeno iz rumenih in modrih kvadratov. Vir: f. Zapata

Kaj je sestavljeno nasledstvo?

A Sestavno nasledstvo Sestavljen je iz zaporedja elementov, ustvarjenih iz dveh (ali več) različnih in nadomestnih nasledstva. Vsak od teh nasledstva ima posebno pravilo, ki se uporablja za iskanje njihovih elementov.

Elementov ni treba biti številčni, saj so sposobni biti figure, simboli ali črke, toda tisti, ki temeljijo na številkah, se imenujejo Aritmetična nasledstvo. Slika, s katero se začne naš članek, prikazuje sestavljeno nasledstvo z rumenih in modrih kvadratov.

V tem nasledstvu se začne z velikega kvadrata, sestavljenega iz 8 rumenih kvadratov in modrega kvadrata. Če želite dobiti naslednji izraz, se na levo ali desno od prve in tretje vrstice kvadratov doda rumen kvadrat. Prostor, ki ima za posledico osrednjo vrsto, je napolnjen z modrim kvadratom.

Vsaka številka v zaporedju se imenuje izraz. Če želite najti peti mandat, morate dodati rumen kvadrat desno od prvega in tretjega razreda ter modri kvadrat v drugi vrsti:

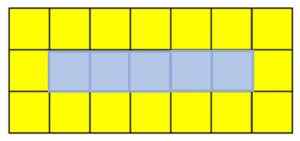Peti mandat zaporedja rumenih in modrih kvadratov. Vir: f. Zapata

Pojasnilo

V sestavljenih nasledjih se izraze pridobijo z izmeničnim pogojem dveh ali več neodvisnih preprostih nasledstva. Če želite bolje razumeti idejo, je treba pregledati podrobnosti o preprostem nasledstvu.

Na primer, naslednje preproste nasledstva sestavljajo naravne številke:

2, 4, 6, 8, 10, 12 ..

Točke suspendiranja kažejo, da ima nasledstvo neskončne izraze.

Vsak od izrazov je označen z majhno črko in številko, kot podpis. Ta številka označuje položaj oz indeks vsakega izraza. V prejšnjem nasledstvu lahko napišete:

do₁ = 2; do₂ = 4; do₃ = 6; do₄ = 8 ..

Zelo priročno je imeti način za izračun katerega koli zaželenega izraza, to je njegovo posebno pravilo. Z njo N-ésimo izraz, tudi Splošni izraz, označeno kot a_n.

Vam lahko služi: lastnosti enakosti

Če nadaljujete z primerom nasledstva celo številk, lahko iz prejšnjega izraza določite način izračuna izraza N-Ésimo:

do_n = a_N-1 + 2

Kje_N-1 Je izraz, ki je pred tem_n.

Seveda bi bilo bolje vedeti splošni izraz brez odvisnosti od drugih pogojev. V tem nasledstvu je enostavno opozoriti, da se kateri koli izraz pomnoži za 2 položaj, ki ga zaseda, glede na podpis izraza. Na ta način je napisano:

do_n = 2n

Starodavni Grki so že poznali zaporedje enakomernih in neparnih številk. Medtem je lahko nasledstvo nenavadnih naravnih številk zapisano kot:

1, 3, 5, 7, 9, 11 ..

In združevanje nasledstva enakomernih številk z neparno je naslednje sestavljeno nasledstvo:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ..

Čigar rezultat je nabor naravnih številk.

Pogoji sestavljenega nasledstva

Morda je zabavno poskušati najti odnos, ki obstaja v zaporedju števil, za katerega je treba skrbno opaziti in poskusiti ugotoviti, ali gre za sestavljeno nasledstvo.

Splošna oblika nasledstva, sestavljena iz dveh nasledstva, bo:

do₁, b₁, do₂, b₂, do₃, b₃, do₄, b₄,..

Kje₁, do₂, do₃, do₄,... so pogoji prvega nasledstva in B₁, b₂, b₃, b₄,… Tisti drugega. Vedno so prepleteni, kot je to v tem primeru:

7, 8, 14, 16, enaindvajset, 24. 24, 28, 32, 35..

Kakšen bo izraz, ki sledi?

Če želite vedeti, poznajte nasledstvo v dveh nadomestnih sklopih številk, kot sledi:

• 7, 14, 21, 28, 35 ..
• 8, 16, 24, 32 ..

V prvem od teh sklopov se pojavijo večkratniki 7:

do₁ = 7 × 1 = 7; do₂ = 7 × 2 = 14; do₃ = 7 × 3 = 21; do₄ = 7 × 4 = 28; do₅ = 7 × 5 = 35

Splošni izraz tega nasledstva je:

do_n = 7n

In v drugem, to so večkratniki 8:

b₁ = 8 × 1 = 8; b₂ = 8 × 2 = 16; b₃ = 8 × 3 = 24; b₄ = 8 × 4 = 32

Torej je njen splošni izraz:

Lahko vam služi: resnična realna spremenljiva funkcija in njegov grafični prikaz

b_n = 8n

Ko se vrne v prvotno sestavljeno nasledstvo, 35 pripada prvemu zaporedju, katerega pogoji so₁, do₂, do₃, do₄ … 35 je peti mandat, zato mora biti izraz, ki sledi₅, ki je enostavno dobiti iz pravila, da bi našli splošni izraz:

b₅ = 8 × 5 = 40

In je napisano:

7, 8, 14, 16, enaindvajset, 24. 24, 28, 32, 35, 40 ..

Primeri sestavljenih nasledstva

Primer 1

Lahko ustvarite sestavljeno nasledstvo z geometrijskimi figurami, kot sta kvadrat in krog, in jih uredite, kot je prikazano spodaj:

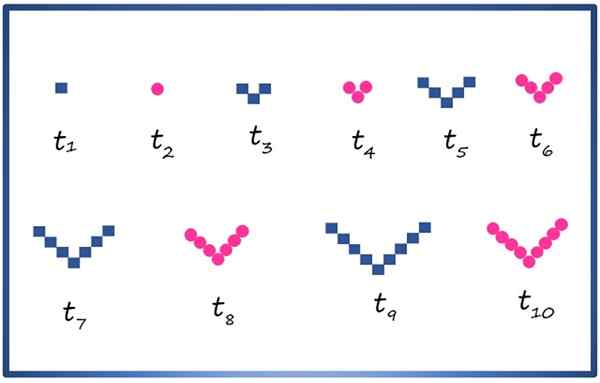Prvih 10 izrazov sestavljenega nasledstva s kvadratnimi geometrijskimi elementi in krogi. Vir: f. Zapata

Vsak izraz je označen s t₁, t₂, t₃, t₄ …, Pogoji indeksa parque -a so sestavljeni iz krogov in tistih, ki so v indeksu, kvadratki. Previdno opazovanje zaporedja je mogoče na primer vedeti, da izraz t_enajst, ki se ne pojavlja na sliki, je sestavljen iz 11 kvadratov z določbo v V.

Primer 2

Naslednje sestavljeno nasledstvo je sestavljeno iz simbolov, v tem primeru črke r in s:

R ss rr sss rrr sss rrrr ssss rrrr ssssss ..

Vsak nov izraz je zgrajen z dodajanjem pisma prejšnjim. Prvi štirje izrazi prikazanega zaporedja so:

t₁= R ; t₂= H.H ; t₃= Rr ; t₄= Sss ..

In naslednji izraz, ki bi se pojavil po prikazanih izrazih, je:

t_enajst= Rrrrrr

Primer 3

Prejšnji primeri so pokazali naraščajoče naslednje, v katerih se vsaka vrednost na nek način poveča glede na prejšnjo. Vendar ni vedno treba biti na ta način, saj se zaporedji lahko spuščajo, to je, da imajo vzorec zmanjšanja.

In naraščajoče naslednje je mogoče kombinirati s padajočimi nasledniki.

Sestavljeno je naslednje numerično nasledstvo:

4, 36, 7, 35, 10, ___, ___, 33, 16, ___, ___, ..

Lahko ga ločimo na dve nasledniki:

• 4, 7, 10, ___, 16, ___, ..
• 36, 35, ___, 33, ___, ..

Katere so vrednosti, ki jih je treba postaviti v prazne prostore?

Previdno opazovanje prvega nasledstva, vsak izraz dobimo z dodajanjem 3 v prejšnji mandat. Zato je naraščajoča naslednja:

Vam lahko služi: kotni premik

7 = 4 + 3

10 = 7 + 3

Zato morate v prvem praznem prostoru postaviti:

10 + 3 = 13

Po tem je v resnici naslednji izraz:

16 = 13 + 3

In tisti, ki gre v drugo prazno, je:

16 + 3 = 19

Drugo nasledstvo se spušča in zelo enostavno je najti manjkajoče izraze, saj opazimo, da se vsak izraz pridobi z odštevanjem 1 od prejšnjega izraza, zato:

36, 35, 3. 4, 33, 32..

Končno lahko napišete:

4, 36, 7, 35, 10, 3. 4, 13, 33, 16, 32, 19,..

Rešene vaje

Vaja 1

V nasledstvu, sestavljenem iz primera 3 v prejšnjem razdelku:

a) Ali 29 pripada omenjenemu nasledstvu?

b) Napišite še 10 pogojev tega nasledstva

Odgovor na

Da, pripada, saj se drugo nasledstvo spušča in njegovi pogoji dobimo z odštevanjem 1 od prejšnjega izraza. Na ta način sčasoma doseže 29.

Odgovor b

4, 36, 7, 35, 10, 34, 13, 33, 16, 32, 19, 31, 22, 25, 29, 28, 31, 27, 34, ..

Upoštevajte, da se nekateri izrazi ponavljajo.

Vaja 2

Poiščite manjkajoče izraze v naslednjem sestavljenem nasledstvu:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, ..

Odgovor

Neparni izrazi so napisani za pridobitev prvega nasledstva:

100, 115, 130, 145, 160, ..

Opazimo, da morate za iskanje vsakega izraza dodati 15 v prejšnji izraz, zato je izraz, ki sledi pri 160, 175.

Drugo nasledstvo je sestavljeno iz:

500, 480, 460, 440, 420, ..

Vsak izraz se razlikuje od prejšnjega do 20, nasledstvo pa se spušča, zato je izraz pri 420 400.

S temi informacijami sta v prvotno sestavljeno nasledstvo dodana še dva izraza, kot je ta:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, 175, 400, ..

Reference

1. Larson, r. (2012). Prekalenkulacija. 8. Izdaja. Cengage učenje.
2. Stewart, J. (2007). Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
3. Sestavljene nasledstva. Obnovi se od: medije.Educacioncampeche.Gob.mx.
4. Numerične nasledstva. Pridobljeno od: matemathweb.com.
5. Zasoji. Aritmetični in geometrijski napredek. Pridobljeno iz: macmillaneducation.je.