SISTEM OPREME REŠITEV REŠITVE METODE, PRIMETI, VASI

The Ekuacijski sistemi Sestavljata dve ali več enačb z več spremenljivkami, ki morajo imeti skupno rešitev. So pogoste, saj v praksi obstajajo številne situacije, ki so odvisne od številnih dejavnikov, ki so povezane na več načinov.

Na splošno ima sistem enačb naslednji obrazec, kjer vsaka funkcija predstavlja enega od pogojev, ki jih mora rešitev izpolnjevati:

Slika 1. Sistem enačb je sestavljen iz funkcij M in n neznank. Vir: f. Zapata.

Poglejmo primer: Recimo, da morate izdelati pravokotne papirnate liste, katerih območje je 180 cm² in imajo obod 54 cm. Kakšne bi morale biti dimenzije lista?

Da bi odgovorili na vprašanje, upoštevamo, da so dimenzije pravokotnega lista dve: široki in visoki. To pomeni, da imamo dve spremenljivki, do katerih bomo dali običajna imena x in in.

In te spremenljivke morajo izpolnjevati dva pogoja, ki sta bila uvedena hkrati:

-Prvi pogoj: Območje lamine je 180 cm². To bo prva funkcija: f₁.

-Drugi pogoj: obod ali kontura lista mora biti 54 cm. To je druga funkcija F₂.

Za vsak pogoj se vzpostavi enačba z uporabo algebrskega jezika. Območje A pravokotnega lista se dobimo tako, da se pomnoži široko:

A = x.y = 180 cm²

In obod P je posledica dodajanja strani. Ker je obod vsota strani:

P = 2x + 2y = 54 cm

Sistem, ki izhaja iz dveh enačb in dveh neznank, je:

Xy = 180

2 (x + y) = 54

Potrebujemo dve številki, katerih izdelek je 180 in da je dvojni produkt njegove vsote 54 ali kaj je enako: Dodano je treba dati 27. Te številke so 12 in 15.

V razdelku Rešene vaje bomo ponudili podrobno metodo za iskanje teh vrednosti, medtem ko lahko bralec zlahka preveri zamenjavo, kar dejansko izpolnjuje obe enačbi.

[TOC]

Primeri aplikacij sistemov enačb

Zgoraj predlagana situacija vsebuje 2 spremenljivki in za njihovo iskanje sta potrebna vsaj 2 enačbi. Obstajajo sistemi z veliko več spremenljivkami, vendar v vsakem primeru, če ima sistem n Od teh je vsaj potrebno n Neodvisne enačbe (ne moremo biti linearna kombinacija drugih) za iskanje rešitve, če obstaja.

Vam lahko služi: vrv (geometrija): dolžina, izrek in vaje

Kar zadeva aplikacije, so številne. Tukaj je nekaj, v katerih sistemi enačb kažejo njihovo uporabnost:

-Poiščite tokove, ki krožijo skozi vezje s pomočjo Kirchoffovih zakonov.

-V kopenskem in zračnem prevozu za določitev urnikov izhoda in prihoda.

-Poiščite veličine sil v dinamičnih ali statičnih sistemih, ki so podvržene večkratnim interakcijam.

-Če želite vedeti, koliko predmetov, ki se prodajajo za določeno obdobje ali v tovarnah.

-Pri določanju, kako razdeliti kapital v več naložbah.

-Vzpostavite stopnje za različne storitve, na primer telekomunikacije ali kažejo in poznajte znesek zbranega denarja (glej primer rešeno 2)

Metode rešitve enačb

Metoda zamenjave

-Izbrana je enačba in ena od spremenljivk je očiščena.

-Potem morate v drugi enačbi zamenjati jasno spremenljivko. Potem ta spremenljivka izgine od tam in če ima sistem dve enačbi in dve neznani, obstaja enačba s spremenljivko, ki je že lahko jasna.

-Če ima sistem več kot dve spremenljivki, morate očistiti tretjino neznano iz druge enačbe in ga tudi zamenjati.

Primer uporabe te metode je v letu razrešen 1.

Metoda zmanjšanja ali izločanja

Ta metoda je sestavljena iz dodajanja ali odštevanja enačb za odpravo ene ali več spremenljivk in zapustitev ene same. Če želite to narediti, je primerno pomnožiti enačbe s faktorjem, tako da z dodajanjem z drugo enačbo neznano izgine. Poglejmo primer:

3x² - in² = 11

Lahko vam služi: Ukrepi za osrednje tendence za združene podatke: formule, vaje

x² + 4y² = 8

Prvo enačbo pomnožimo s 4:

12x² - 4y² = 44

x² + 4y² = 8

Z dodajanjem neznanega izginite in, ostati:

13x² = 52

x² = 4

Zato x₁ = 2 in x₂ = -2. S temi vrednostmi lahko bralec to preveri in₁ = 1 in₂ = -1

Metoda izravnave

Ko je sistem dve enačbi z dvema neznankoma:

-Neznano je izbrano in razčisti obe enačbi.

-Rezultati so izenačeni, kar omogoča pridobivanje ene enačbe z enim neznanim.

-Ta enačba je razrešena in rezultat se nadomesti v eni od prejšnjih jaslic, da dobimo vrednost drugega neznanega.

Ta metoda bo uporabljena v letu Rešena 2 od naslednjega oddelka.

Grafična metoda

Ta metoda je sestavljena iz grafice krivulj, ki jih predstavlja vsaka enačba. Točka presečišča je sistemska rešitev. Naslednji primer prikazuje grafično rešitev sistema:

x² + in ² = 1

2x + 4y = 0

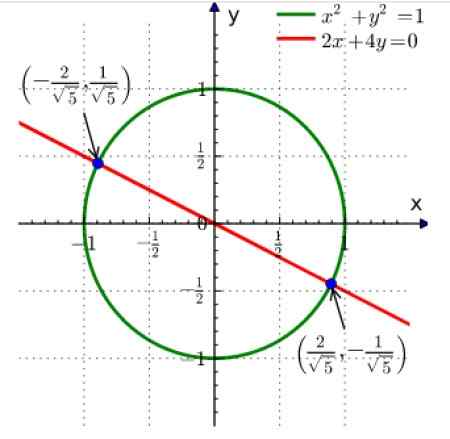Slika 2. Grafična rešitev sistema sočasnih enačb je najti presečišče krivulj. Vir: Wikimedia Commons.

Prva enačba je krog polmera 1, osredotočen na izvor, druga.

Presečišče obeh sta dve točki, prikazani v modri barvi. Bralec lahko preveri, da z zamenjavo koordinat točk v zgornjih enačbah dobimo enakost.

Vaje

- Vaja rešena 1

Morate izdelati pravokotne liste 180 cm² in s 54 cm obod. Kakšne bi morale biti dimenzije lista?

Rešitev

Sistem, ki ga je treba rešiti, je:

Xy = 180

2 (x + y) = 54

Druga enačba je mogoče poenostaviti na x + y = 27, torej:

Xy = 180

x + y = 27

Ena od neznank druge enačbe je očiščena:

y = 27 - x

Odmik je zamenjan v prvem:

(27 -x) = 180

Uporaba distribucijske lastnosti:

-x² + 27x = 180

Pomnoževanje z (-1) na obeh straneh enačbe in pošiljanje 180 na levo stran:

x² - 27x +180 = 0

To je enačba druge stopnje v X, ki jo reši formula:

Lahko vam služi: nasproti kotov z točko (z rešeno vajo)

Z a = 1, b = -27 in c = 180

 Rešitve so: x₁ = 15 cm in x₂ = 12, zato so dimenzije y in₁ = 12 cm in in₂ = 15 cm.

- Vaja Rešena 2

Zabavni park ima naslednje stopnje na vhod: Otroci 1.5 in odrasli 4 USD. V enem dnevu je bilo 2200 obiskovalcev in zbralo 5050 dolarjev. Poiščite število otrok in odraslih, ki so tisti dan obiskali park.

Slika 3. Sistem enačb služi za razčlenitev zbirke zabaviščnega parka v enem dnevu. Vir: Pixabay.

Rešitev

Biti x Število otrok in in Število odraslih. Lahko vzpostavimo prvo od enačb, ki vedo, da mora biti vsota obeh 2200:

x + y = 2200.

Zdaj gremo z zbranim denarjem. Cena vstopnice za otroke je 1.5 $ za vsakega otroka, tako da bomo to vrednost pomnožili s X, številom otrok, bomo imeli znesek za vnos otrok:

1.5x = denar, ki ga zbirajo otroške vstopnice

In če pomnožimo 4 USD na odraslo osebo za količino in odrasle obiskovalce, skupni denar pridobijo vsi odrasli:

4y = denar, zbran z vstopnicami za odrasle

To dodamo, da dobimo 5050 USD:

1.5x + 4y = 5050

Naš sistem enačb je:

x + y = 2200

1.5x + 4y = 5050

Rešimo ga z izenačenjem. Očistimo spremenljivko in prvo in drugo enačbo:

y = 2200 - x

y = (5050 - 1.5 x) /4

Oba izražanja: enaka:

2200 - x = (5050 - 1.5x) /4

Vse pomnožimo s 4, da odpravimo del:

8800 - 4x = 5050 - 1.5x

Izrazi združimo z X na levi in ​​čiste številke na desni:

-4x + 1.5x = 5050 - 8800

-2.5x = -3750

x = 1500 otrok.

To vrednost nadomestimo pri y = 2200 - x, da poznamo število odraslih:

y = 2200 - 1500 = 700 odraslih.

Reference

1. CK-12. Sistemi enačb in neenakosti. Okreval od: CK12.org.
2. Hoffman, J. Izbira vprašanj matematike. Zvezek 2.
3. Jiménez, r. 2008. Algebra. Dvorana Prentice.
4. Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
5. Zill, d. 1984. Algebra in trigonometrija. McGraw Hill.