Lastnosti, primeri in vaje aksialne simetrije

The Aksialna simetrija Pojavi se, ko točke slike sovpadajo s točkami druge številke s pomočjo ravne mediatrike, imenovane simetrična os. Imenuje se tudi radialna, rotacijska ali cilindrična simetrija.

Običajno se uporablja v geometrijskih figurah, vendar je v naravi zlahka opaziti, saj obstajajo živali, kot so metulji, škorpijoni, police ali pravilno ljudje, ki predstavljajo aksialno simetrijo.

Na tej fotografiji obzorja mesta Toronto je razstavljen njen odsev v vodni aksialni simetriji. (Vir: Pixabay)

[TOC]

Kako najti simetrično aksialno

Za iskanje simetričnega osnega p 'p točke glede na črto (l) se izvede naslednje geometrijske operacije:

1.- Sledi pravokotna na črto (l), ki poteka skozi točko P.

2.- Prestrezanje obeh vrstic določa točko oz.

3.- Dolžina segmenta PO se meri, nato se ta dolžina kopira na črto (PO), ki se začne iz ali v smeri p a ali določi točko p '.

4.- Točka str.

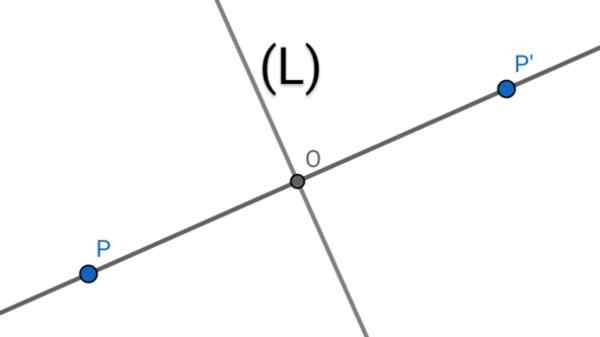Slika 1. Dve točki P in P 'sta osno simetrični do osi (l), če je omenjena os mediatriksa PP segmenta'

Lastnosti osne simetrije

- Aksialna simetrija je izometrična, to je razdalja geometrijske figure in njegove ustrezne simetrične.

- Mera kota in njenega simetričnega sta enaka.

- Simetrična os točke na osi simetrije je točka sama.

Lahko vam služi: Gauss-Seidel Metoda: Pojasnilo, aplikacije, primeri

- Simetrična črta črte, vzporedno z osi simetrije.

- Sekanska črta do osi simetrije je simetrična.

- Simetrična slika črte je še ena črta, ki tvori kot z osi simetrije istega ukrepa kot originalna črta.

- Simetrična slika črte, pravokotne na os simetrije, je še ena črta, ki prekriva prvo.

- Črta in njegova osna simetrična črta tvorita kot, katerega bisektor je os simetrije.

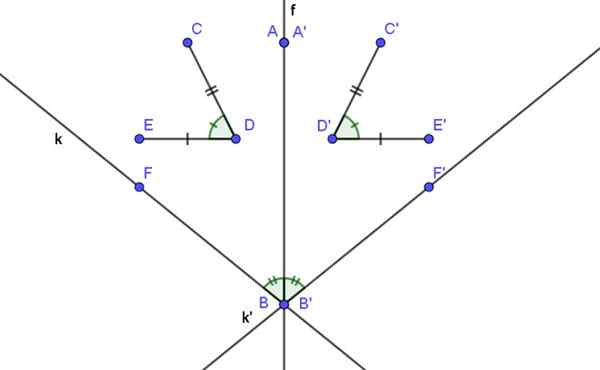Slika 2. Aksialna simetrija ohranja razdalje in kote.

Primeri aksialne simetrije

Narava ima obilne primere aksialne simetrije. Na primer, med številnimi drugimi lahko vidite simetrijo obrazov, žuželk, kot so metulji, odsev na površinah mirnih voda in ogledal ali listi rastlin.

Slika 3. Ta metulj ima skoraj popolno aksialno simetrijo. (Vir: Pixabay) Slika 4. Obraz te deklice ima aksialno simetrijo. (Vir: Pixabay)

Vaje za aksialno simetrijo

Vaja 1

Imate trikotnik tokov A, B in C, katerih kartezijanske koordinate so A = (2, 5), B = (1, 1) in C = (3.3). Poiščite kartezijanske koordinate simetričnega trikotnika glede na osi y (os ordinatov).

Rešitev: Če ima točka P koordinate (x, y), potem je njegova simetrična glede na osi ordinatov (osi y) p '= (-x, y). Z drugimi besedami.

Vam lahko služi: neskončni niz: lastnosti, primeri

V tem primeru bodo imeli simetrični trikotnik tokov a ', b' in c 'koordinate:

A '= (-2, 5); B '= (-1, 1) in c' = (-3, 3), kot je mogoče preveriti na sliki 6.

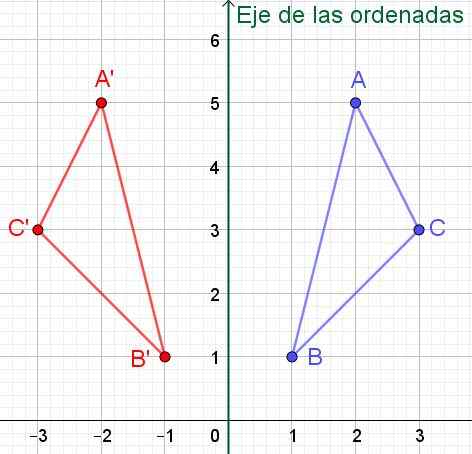Slika 6. Če ima točka koordinate (x, y), simetrično glede na osi y (os ordinatov) bo imela koordinate (-x, y).

Vaja 2

Glede na trikotnik ABC in njegov simetrični a'b'c 'vaje 1 preverite, ali imajo ustrezne strani originalnega trikotnika in njene simetrične enake dolžine.

Rešitev: Za iskanje razdalje ali dolžine strani uporabljamo formulo Euclidian razdalje:

d (a, b) = √ ((bx-as)^2 + (by-ay)^2) = √ ((1-2)^2 + (1-5)^2) = √ ((-1 )^2 + (-4)^2) = √ (17) = 4.123

Nato se izračuna dolžina simetrične strani, ki ustreza'b ':

D (a ', b') = √ ((bx'-ax ')^2 +(by'-y^2) = √ ((-1 +2)^2 +(1-5)^2) = √ ((1)^2 + (-4)^2) = √ (17) = 4,123

Na ta način je dokazano, da aksialna simetrija ohranja razdaljo med dvema točkama. Postopek se lahko ponovi za drugi dve strani trikotnika in njegovo simetrično, da preverite invariance v dolžini. Na primer | AC | = | A'c '| = √5 = 2,236.

Vaja 3

V zvezi s trikotnikom ABC in njegovim simetričnim A'B'c 'vaje 1 preverite, ali imajo ustrezni koti prvotnega trikotnika in njihovega simetričnega istega kotnega ukrepa.

Rešitev: Za določitev ukrepov kotov BAC in B'a'c 'bo najprej izračunan skalarni produkt vektorjev Ab z AC in potem skalarni produkt A'B ' z A'C '.

Spominjanje tega:

A = (2, 5), b = (1, 1) in c = (3.3)

A '= (-2, 5); B '= (-1, 1) in c' = (-3, 3).

Imaš:

Ab = y AC =

podobno

A'B ' = y AC =

Vam lahko služi: lamy teorem

Nato najdemo naslednje skalarne izdelke:

ABVAC = ⋅ = -1⋅1 + (-4) ⋅ (-2) = -1 + 8 = 7

podobno

A'B'⋅a'c ' = ⋅ = 1⋅ (-1) + (-4) ⋅ (-2) = -1 + 8 = 7

Ukrep kota BAC je:

∡Bac = arccos ( ABVAC / (|AB |⋅ |AC |)) = 

Arccos (7 / (4,123⋅2,236)) = 40,6 °

Podobno je merilo kota B'a'c ':

∡b'a'c '= arccos ( A'B'⋅a'c ' / (|A'B '|⋅ |A'c '|)) = 

Arccos (7 / (4,123⋅2,236)) = 40,6 °

Sklepa, da aksialna simetrija ohranja merilo kotov.

Vaja 4

Biti točka p koordinate (a, b). Poiščite koordinate njegovega simetričnega aksialnega p 'glede na črto y = x.

Rešitev: Poklicali bomo (a ', b') na koordinate simetrične točke p 'glede na črto y = x. V sredini točke M segmenta PP 'ima koordinate ((A+A')/2, (B+B ')/2) in je tudi na črti y = x, zato je izpolnjena naslednja enakost:

A + a '= b + b'

Po drugi strani ima segment PP 'v teku -1, da je pravokoten na črto y = x naklona 1, zato je izpolnjena naslednja enakost:

B - b '= a' -a

Odstranjevanje obeh enakosti pred 'in B' je sklenjeno, da:

a '= b in kaj B' = a.

To pomeni, da glede na točko p (a, b) njegovo simetrično osno glede na črto y = x je p '(b, a).

Reference

1. Arce m., Blázquez s in drugi. Ravninske transformacije. Okrevano od: eductmxli.Datoteke.WordPress.com
2. CC izračun. Aksialna simetrija. Iztegnjeno od: izračun.DC
3. Superprof. Aksialna simetrija. Okrevano od: Superprof.je
4. Wikipedija. Aksialna simetrija. Okrevano od: je.Wikipedija.com
5. Wikipedija. Simetrična krožna. Pridobljeno iz: v.Wikipedija.com