Niz primerov moči in vaje

A Serija moči Sestavljen je iz vsote izrazov v obliki moči spremenljivke x, ali bolj na splošno X-c, kje c To je stalno resnično število. V povzetku vsote se niz moči izraža na naslednji način:

∑a_n (X -c)ⁿ = a_tudi + do₁ (x - c) + a₂ (X - c)² + do₃ (X - c)³ +… + A_n (X - c)ⁿ

Kjer koeficienti_tudi, do₁, do₂… So resnične številke in serija se začne pri n = 0.

Slika 1. Opredelitev serije moči. Vir: f. Zapata.

Ta serija je osredotočena na vrednost c to je konstantno, vendar lahko to izberete c Biti enak 0, v tem primeru so pooblastila poenostavljena:

∑a_n xⁿ = a_tudi + do₁ x + a₂ x² + do₃ x³ +… + A_n xⁿ

Serija se začne z do_tudi(X-c)⁰ in do_tudix⁰ oziroma. Ampak to vemo:

(X-c)⁰= x⁰ = 1

Zato do_tudi(X-c)⁰ = do_tudix⁰ = do_tudi (Neodvisen izraz)

Dobra stvar pri silah moči je, da lahko z njimi izrazite funkcije in to ima številne prednosti, še posebej, če želite sodelovati z zapleteno funkcijo.

Ko je temu tako, se namesto neposredne uporabe uporabi njegov razvoj moči, ki ga je mogoče lažje izpeljati, integrirati ali delati številčno.

Seveda je vse pogojeno s konvergenco serije. Serija se zbliža, ko z dodajanjem določene količine izrazov dobimo fiksno vrednost. In če dodamo več izrazov, še naprej pridobimo to vrednost.

[TOC]

Funkcije kot pooblastila

Kot primer funkcije, izražene kot niz moči, vzemimo f (x) = e^x.

To funkcijo je mogoče izraziti v smislu vrste moči, kot sledi:

in^x  ≈ 1 + x + (x² / 2!) + (X³ / 3!) + (x⁴ / 4!) + (x⁵ / 5!) +..

Kje! = n. (N-1). (N-2). (N-3)… in vzeta je 0! = 1.

Preverili bomo s pomočjo kalkulatorja, ki serija učinkovito sovpada z izrecno dano funkcijo. Na primer, začnimo delati x = 0.

Vam lahko služi: teoretična verjetnost: kako jo izvleči, primeri, vaje

Vemo, da E⁰ = 1. Poglejmo, kaj počne serija:

in⁰ ≈ 1 + 0 + (0² / 2!) + (0³ / 3!) + (0⁴ / 4!) + (0⁵ / 5!) +… = 1

In zdaj poskusimo z x = 1. Kalkulator to vrže in¹ = 2.71828, In potem primerjamo s serijo:

in¹ ≈ 1 + 1 + (1² / 2!) + (1³ / 3!) + (1⁴ / 4!) + (1⁵ / 5!) +… = 2 + 0.5000 + 0.1667 + 0.0417 + 0.0083 +… ≈ 2.7167

S samo 5 izrazi že imamo natančno naključje E ≈ 2.71. Naša serija manjka le malo več, a ko je dodanih več izrazov, se z vso gotovostjo serija zbliža v natančno vrednost in. Reprezentacija je natančna, kdaj N → ∞.

Če se predhodna analiza ponovi za n = 2 Pridobljeni so zelo podobni rezultati.

Na ta način smo prepričani, da je eksponentna funkcija f (x) = e^x Lahko ga predstavlja ta niz moči:

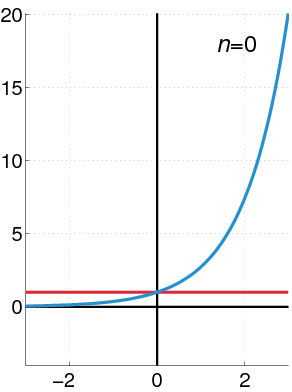Slika 2. V tej animaciji se vidi, saj so moči bližje eksponentni funkciji, saj se sprejmejo več izrazov. Vir: Wikimedia Commons.

Geometrijske moči moči

Funkcija f (x) = e^x To ni edina funkcija, ki priznava serijsko predstavitev moči. Na primer funkcija  F(x) = 1/1 - x  Videti je veliko kot znani Konvergentna geometrijska serija:

∑a.rⁿ = A / 1 - r

Samo naredite a = 1 in r = x, da pridobite primerno serijo v tej funkciji, ki je osredotočena na c = 0:

Vendar je znano, da je ta serija konvergentna za │r│<1, por lo tanto la representación es válida únicamente en el intervalo (-1,1), aunque la función sea válida para todo x, excepto x=1.

Ko želite to funkcijo določiti v drugem intervalu, se preprosto osredotoči na ustrezno vrednost in pripravljeno.

Kako najti serijo razvoja moči funkcije

Vsako funkcijo je mogoče razviti v vrsti moči, osredotočenih na C, dokler ste izhajali iz vseh naročil pri x = c. Postopek uporablja naslednji izrek, imenovan Taylor teorem:

Naj bo F (x) funkcija z derivati ​​naročila n, označeno kot F^(N), ki priznava serijski razvoj moči v intervalu Yo. Njegov razvoj v Serija Taylor je:

Lahko vam služi: kakšna je lokacija celih in decimalnih številk?

Tako da:

f (x) = f (c) + f '(c) (x-c) + f "(c) (x-c)² /2 + f "(c) (x-c)³ /6 +… r_n

Kjer r_n, ki je n. serije, se imenuje ostanek:

Ko se C = 0 pokliče serija Serija Maclaurin.

Ta serija je tukaj enaka serijam, ki je bila podana na začetku, šele zdaj obstaja način, kako izrecno najti koeficiente vsakega izraza, ki ga daje:

Vendar je treba zagotoviti, da serija prenaša funkcijo, ki jo želite predstavljati. Zgodi se, da se vsaka Taylorjeva serija nujno ne približa F (x), ki je bila v mislih pri izračunu koeficientov do_n.

To se zgodi, ker so morda tisti, ki izhajajo iz funkcije, ocenjeni v x = c sovpada z isto vrednostjo tistih, ki izhajajo iz drugega, tudi v x = c. V tem primeru bi bili koeficienti enaki, vendar bi bil razvoj dvoumen, če ne bi imel gotovosti, katere funkcije ustreza.

Na srečo obstaja način, kako vedeti:

Merila za konvergenco

Da se izognemo dvoumnosti, če r_n → 0 Ko je n → ∞ za vse x v intervalu I, se serija konvergira na f (x).

Vaja

- Vaja rešena 1

Poiščite geometrijske moči za funkcijo f (x) = 1/2 - x osredotočen na C = 0.

Rešitev

Dana funkcija mora biti izražena na način, ki se čim bolj ujema z 1 / 1- x, katere serija je znana. Zato prepišemo števca in imenovalec, ne da bi spremenili izvirni izraz:

1/2 - x = (1/2) / [1 - (x / 2)]

Ker je ½ konstantno, gre iz vsote in to je napisano v smislu nove spremenljivke x/2:

Vam lahko služi: konjugirani binomial: kako je rešena, primeri, vaje

Upoštevajte, da x = 2 ne spada v domeno funkcije in v skladu s konvergenčnimi merili, navedenimi v razdelku Power Geometric Series, Razvoj velja za │x/2│< 1 o equivalentemente -2 < x < 2.

- Vaja Rešena 2

Poiščite prvih 5 izrazov Maclaurina serije Razvoj funkcije f (x) = sen x.

Rešitev

Korak 1

Najprej so derivati:

-Izhaja iz vrstnega reda 0: je enaka funkcija f (x) = sen x

-Prva derivat: (sin x) '= cos x

-Drugi izpeljan: (sin x) "= (cos x) '= - sin x

-Tretja derivat: (sin x) "= (-sen x) '= - cos x

-Četrti derivat: (sin x) "= (- cos x) '= sin x

2. korak

Potem se vsak derivat oceni pri x = c, prav tako tudi razvoj maclaurina, c = 0:

greh 0 = 0; cos 0 = 1; - sen 0 = 0; -Cos 0 = -1; greh 0 = 0

Korak 3

Koeficienti so zgrajeni na_n;

do_tudi = 0/0! = 0; do₁ = 1/1! = 1; do₂ = 0/2! = 0; do₃ = -1 / 3!; do₄ = 0/4! = 0

4. korak

Končno je serija sestavljena v skladu z:

greh x ≈ 0.x⁰ + 1. x¹ + 0 .x² - (1/3!) x³ + 0.x⁴... = x - (1/3!)) x³  +..

Ali bralec potrebuje več izrazov? Koliko jih je več, serija je bližje funkciji.

Upoštevajte, da je v koeficientih vzorec, naslednji ne -nulski izraz je₅ In ves indeks neparnega indeksa se razlikuje tudi od 0, izmenično znake, tako da:

Sen x ≈ x - (1/3!)) x³  + (1/5!)) x⁵ - (1/7!)) x⁷  +.. .

Ostane kot vaja za preverjanje, lahko uporabite Razmerje količnika Za konvergenco serije.

Reference

1. Fundacija CK-12. Serija moči: predstavitev funkcij in operacij. Okreval od: CK12.org.
2. Engler, a. 2019. Integralni računanje. Nacionalna univerza na obali.
3. Larson, r. 2010. Izračun spremenljivke. 9na. Izdaja. McGraw Hill.
4. Brezplačna besedila matematike. Serija moči. Okrevano od: matematika.LiibreTexts.org.
5. Wikipedija. Serija moči. Okrevano od: je.Wikipedija.org.