Sturges pravilo

Pojasnjujemo, kaj je pravilo Sturgesa, njegova uporaba in daje več primerov

Kaj je pravilo Sturgesa?

The Sturges pravilo To je merilo, ki se uporablja za določitev števila razredov ali intervalov, ki so potrebni za grafiko nabora statističnih podatkov. To pravilo je leta 1926 navedel nemški matematik Herbert Sturges.

Sturges je predlagal preprosto metodo, ki temelji na številu vzorcev X, ki so omogočili iskanje števila razredov in njihov razpon razpona. Pravilo Sturges se pogosto uporablja predvsem na območju statistike, zlasti za izdelavo frekvenčnih histogramov.

Pojasnilo

Pravilo Sturges je empirična metoda, ki se pogosto uporablja v opisni statistiki za določitev števila razredov, ki morajo obstajati v frekvenčnem histogramu, za razvrstitev nabora podatkov, ki predstavlja vzorec ali populacijo.

V bistvu to pravilo določa širino grafičnih posod, frekvenčne histograme.

Da bi vzpostavil svoje pravilo, je Herbert Sturges veljal za idealen frekvenčni diagram, ki ga sestavljajo K intervali, kjer I -ta interval vsebuje določeno število vzorcev (i = 0,… k - 1), predstavljen kot:

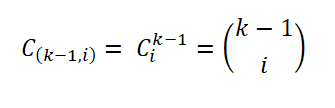
To število vzorcev je podano s številom načinov, kako lahko izvlečemo podskupino nabora; To pomeni, da je s binomskim koeficientom izraženo na naslednji način:

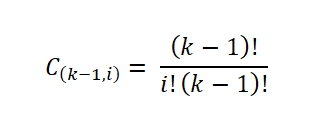Nato se je Sturges navajal, da bo frekvenčni histogram približal normalno porazdelitev, ko se število intervalov (k) poveča v skladu z osrednjim teoremom meje. Na tak način, da je mogoče izračunati število vzorcev vsakega od intervalov:

Lahko vam služi: Enegon: Lastnosti, kako narediti enegon, primeri

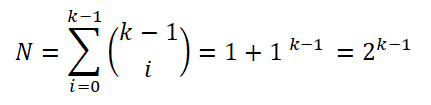
Za poenostavitev izraza je uporabil lastnosti logaritmov v obeh delih enačbe:

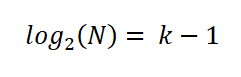
Tako je Sturges ugotovil, da je optimalno število K intervalov dano z izrazom:

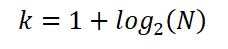
Lahko se izrazi tudi kot:

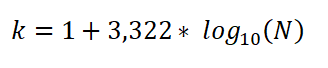
V tem izrazu:

• K je število razredov.
• N je skupno število opazovanj v vzorcu.
• Dnevnik je skupni osnovni logaritem 10.

Na primer, da bi natančno opredelili frekvenčni histogram, ki izraža naključni vzorec stasa 142 otrok, je število intervalov ali razredov, ki jih bo imela porazdelitev,:

K = 1 + 3,322 _* dnevnik₁₀ (N)

K = 1+3,322_* Dnevnik (142)

K = 1+3,322_* 2.1523

K = 8,14 ≈ 8

Tako bo porazdelitev v 8 intervalih.

Število intervalov mora biti vedno predstavljeno s celotnimi številkami. V primerih, ko je vrednost decimalna, je treba približati najbližji celotni številki.

Sturges pravila prijave

Pravilo Sturges se uporablja predvsem v statistiki, saj omogoča porazdelitev frekvence z izračunom števila razredov (k), pa tudi dolžino vsakega od teh, znanih tudi kot amplituda.

Amplituda je razlika v zgornji in spodnji meji razreda, deljena s številom razredov in je izražena:

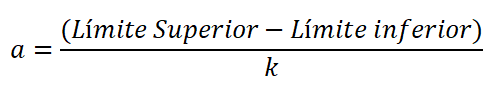
Obstaja veliko empiričnih pravil, ki omogočajo porazdelitev frekvence. Vendar se pravilo Sturgesa običajno uporablja, ker naredi približek števila razredov, ki običajno gre od 5 do 15.

Na ta način meni, da je vrednost, ki pravilno predstavlja vzorec ali populacijo; To pomeni, da pristop ne predstavlja ekstremnih skupin, niti ne deluje s pretiranim številom razredov, ki ne omogočajo povzema vzorca.

Lahko vam služi: nasproti kotov z točko (z rešeno vajo)

Primer

Frekvenčni histogram je treba izvesti v skladu z danimi podatki, ki ustrezajo starosti, pridobljenim v anketi moških, ki telovadijo v lokalni gimnaziji.

Za določitev intervalov je treba poznati velikost vzorca ali število opazovanj; V tem primeru jih je 30.

Potem velja pravilo Sturgesa:

K = 1 + 3,322 _* dnevnik₁₀ (N)

K = 1+3,322_* Dnevnik (30)

K = 1+3,322_* 1.4771

K = 5,90 ≈ 6 intervalov.

Iz števila intervalov lahko izračunate amplitudo, ki jo bodo imeli; to pomeni, da je širina vsake palice, predstavljena v frekvenčnem histogramu:

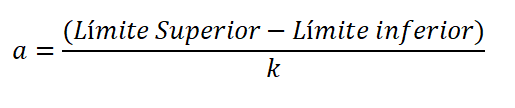
Spodnja meja se šteje za spodnjo vrednost podatkov, zgornja vrednost pa je najvišja vrednost. Razlika med zgornjo in spodnjo mejo se imenuje območje ali pot spremenljivke (r).

Tabela ima, da je zgornja meja 46, spodnja pa 13; Na ta način bo amplituda vsakega razreda:

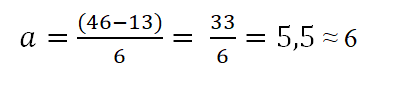
Intervali bodo sestavljeni iz zgornje in spodnje meje. Za določitev teh intervalov se začne s štetjem od spodnje meje in k temu dodaja amplitudo, določeno s pravilom (6), kot sledi:

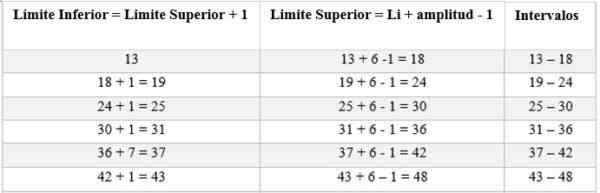
Potem se izračuna absolutna frekvenca, da se določi število moških, ki ustrezajo vsakemu intervalu; V tem primeru je:

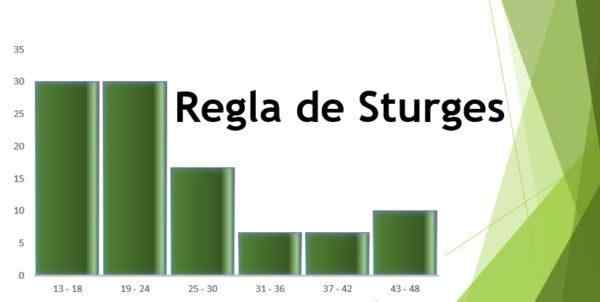
• Interval 1: 13 - 18 = 9
• Interval 2: 19 - 24 = 9
• Interval 3: 25 - 30 = 5
• Interval 4: 31 - 36 = 2
• Interval 5: 37 - 42 = 2
• Interval 6: 43 - 48 = 3

Z dodajanjem absolutne frekvence vsakega razreda mora biti to enako skupnemu številu vzorca; V tem primeru 30.

Vam lahko služi: negativna homotecia

Nato se izračuna relativna frekvenca vsakega intervala, ki deli absolutno frekvenco tega s skupnim številom opazovanj:

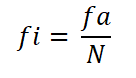
• Interval 1: fi = 9 ÷ 30 = 0.30
• Interval 2: fi = 9 ÷ 30 = 0.30
• Interval 3: fi = 5 ÷ 30 = 0,1666
• Interval 4: fi = 2 ÷ 30 = 0,0666
• Interval 5: fi = 2 ÷ 30 = 0,0666
• Interval 4: fi = 3 ÷ 30 = 0,10

Nato lahko naredite tabelo, ki odraža podatke, in tudi diagram iz relativne frekvence glede na dobljene intervale, kot je razvidno iz naslednjih slik:

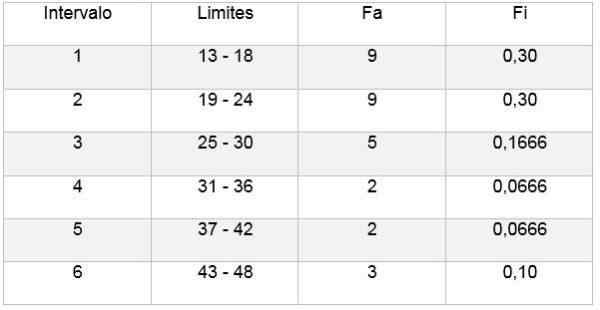
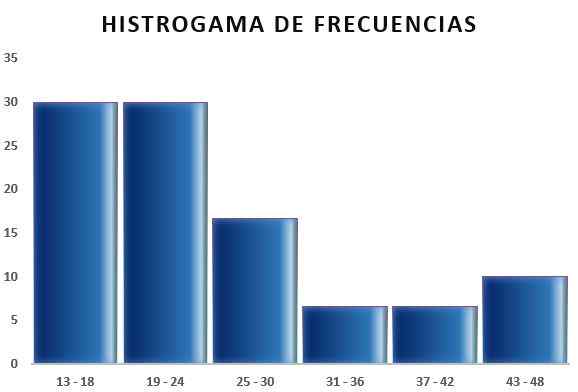
Na ta način pravilo Sturgesa omogoča določitev števila razredov ali intervalov, v katerih je mogoče vzorec razdeliti, da bi povzeli vzorec podatkov z izdelavo tabel in grafike.