Pravilo dopisovanja funkcije

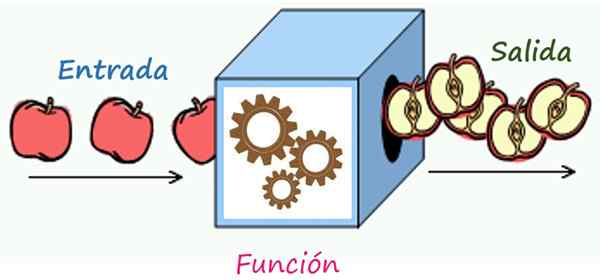
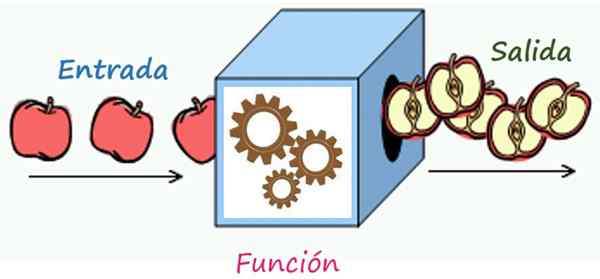Pravilo dopisovanja je mehanizem, ki pretvori elemente vstopa v izhodne elemente. Vir: Wikimedia Commons/F. Zapata

Kakšno je pravilo dopisovanja funkcije?

The pravilo dopisovanja funkcije Opozorite način, kako so elementi enega sklopa povezani z elementi drugega. Elementi prvega niza so znani kot domena, in tistim drugim, kot je Kodominij tudi Contraminium.

Razmerje ali povezavo med sklopi lahko določite z besednim ali pisnim navodilom, če pa so sklopi številčni, je pravilo o dopisovanju označeno s formulo.

Ta formula vsebuje operacije, ki jih je treba izvesti z elementi začetne sklope in s tem pridobiti vrsto elementov, vključenih v kodominium.

Zdaj, ko je razmerje med elementi funkcija, pravilo dopisovanja izpolnjuje dva posebna pogoja:

• Za vsak element domene je povezan s pravilom dopisovanja en sam element kodominija, znan kot slika.
• Ta slika je edinstvena, z drugimi besedami, noben element domene ni povezan z več kot enim elementom kodominija.

Na ta način si lahko predstavljate pravilo o dopisovanju funkcije kot mehanizma, zaklenjenega v polje. Vsaka domena vrednost, brez izjeme, lahko vstopi v polje in se iz njega pretvori, skozi operacije, ki jih označuje pravilo dopisovanja. Primeri bomo videli takoj.

Primeri

Primer 1

Pravilo dopisovanja funkcije lahko izrazimo kot pisno navodilo, ko elementi niso numerični.

Na primer, na voljo je nabor držav, označenih kot P, in drug sklop mest C:

Lahko vam služi: u -test od Manna - Whitney: kaj je to in ko se uporablja, izvedba, primer

P = Kanada, Mehika, Španija, ZDA, Francija, Argentina, Brazilija, Nemčija

C = Paris, London, Buenos Aires, Berlin, Mexico City, Ottawa, Río, New York, Madrid, Washington, Bern, Rim, Brasilia, Toronto

Biti pravilo dopisovanja F Med P in C, ki ga daje:

F: P → c

Kje F To je pravilo "... čigar kapital je .. ”, Ki vsako državo povezuje v P (začetni niz), s svojim glavno mestom v C (nabor prihoda).

Na primer: »Španija, čigar kapital je Madrid ". Element "Španije" pripada začetnemu nastavitvi P, in elementu "Madrid" celotnemu C, prihodu.

Predstavitev te funkcije je mogoče izvesti s pomočjo Vennovega diagrama ali preprosto prek urejenih parov.

Naročeni pari vsebujejo, kot že ime pove, dva elementa z določenim vrstnim redom, v tem primeru je prvi element para država in drugi, njegovo glavno mesto.

Vennov diagram je način za vizualizacijo funkcije, ki prikazuje začetne in nabore prihoda, pa tudi pravilo dopisovanja med njimi.

Predstavitev F kot urejene pare

F = (Kanada, Ottawa); (Mehika, Mexico City); (Španija Madrid); (ZDA; Washington); (Pariz, Francija); (Argentina Buenos Aires); (Brazil Brasilia); (Nemčija, Berlin)

Prvi par sodeluje Kanado, čigar kapital je Ottawa, drugi sodelavci Mehika, čigar kapital je Mexico City in tako naprej.

Predstavitev F kot Vennov diagram

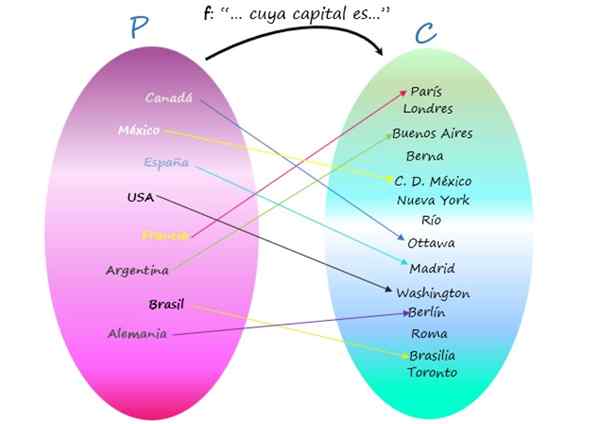
Upoštevajte, da obstajajo mesta, ki niso glavno mesto nobene države, saj, čeprav so elementi kodominija, niso podoba nobenega elementa začetnega niza. Kljub temu je odnos funkcija, saj je pomembno, da ima vsaka država svoj kapital, in to je edinstveno.

Vam lahko služi: območje rednega in nepravilnega pentagona: kako se jemlje, vaje

Podvrsta, ki jo tvorijo elementi kodominija, ki so podoba nekega elementa domene, se imenuje obseg ali funkcija funkcije. Za primer pot r F je:

R = Paris, Buenos Aires, Mexico City, Ottawa, Madrid, Berlin, Washington, Brasilia

Vredno se je vprašati, ali je mogoče vzpostaviti razmerje med C in P, kjer C postane začetni niz in prihod. Odgovor je pritrdilen, vendar ne bi bila funkcija, saj obstajajo mesta, ki niso prestolnica, kot je New York, ali država, za katero so kapital, se ne pojavlja med elementi P kompleksa, kot je Rim.

Primer 2

Ko sta nabor odhoda in nabor prihodov številčna, je pravilo dopisovanja funkcije, ki jih povezuje. Na primer, mojstrstvo funkcije Naslednji niz:

D = 0, 1, 2, 3, 4, 5, 6)

Pravilo dopisovanja F: D → R, ki povezuje elemente D z naborom resničnih števil R je:

F: "Dvojno"

Če je "x" element začetnega niza, je F (x) ustrezen element nabora prihoda in pravilo dopisovanja je napisano tako:

f (x) = 2x

Kodominium je niz realnih številk. Podmnožica reaisov je pot te funkcije, nabor števil, katerih vrednost je dvakrat od x:

R = 0, 2, 4, 6, 8, 10, 12

V obliki urejenih parov ima pravilo dopisovanja:

F = (0,0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Naročeni pari so lahko grafiko na kartezijanski ravnini. Prvi element navora je nameščen na vodoravni osi, imenovan tudi os osi abscis ali osi "x", medtem ko se druga na navpični osi, osi urejene ali preprosto osi "y":

Vam lahko služi: distribucijska lastnina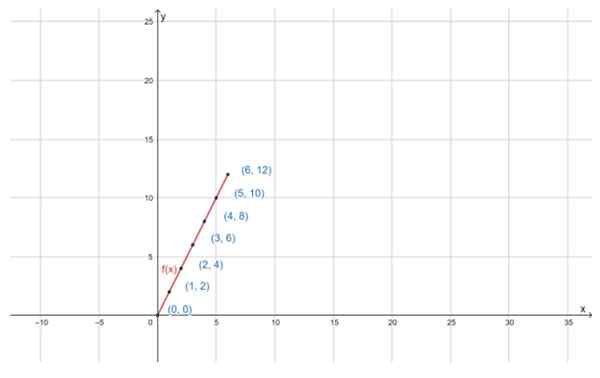 Graf funkcije f (x) = 2x za določeno d domeno je ravna črta. Vir: f. Zapata skozi Geogebro

Vaje

Določite pravilo o dopisovanju za naslednja razmerja, kar kaže, ali gre za funkcije. Nabor naravnih števil je n in resnična je r.

V primerih, v katerih ustreza, navedite tudi domeno, kodominium in pot funkcije:

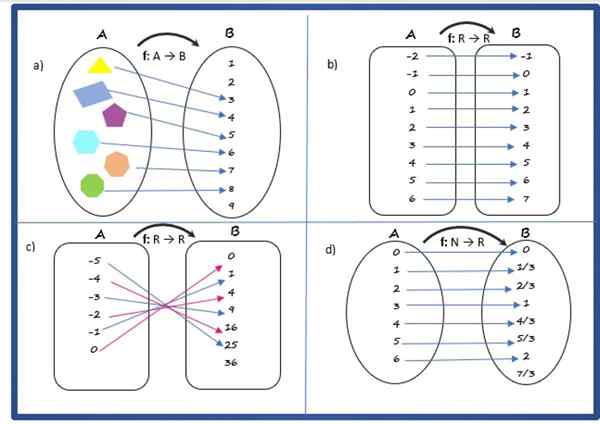
Rešitev

To je funkcija, saj ima vsak element začetnega niza, sestavljen iz poligonov, edinstveno sliko v naboru prihoda.

Pravilo dopisovanja nanaša poligon s številom strani, domeno je sestavljeno iz niza A poligonov:

A = trikotnik, štirikoles

Kodominium je niz prvih naravnih števil, vključno z 0.

B = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

In Co C so naravne številke od 3 do 8:

C = 3, 4, 5, 6, 7, 8

Rešitev b

Je funkcija, saj izpolnjuje zgoraj navedene pogoje.

Pravilo dopisovanja je:

f (x) = x + 1

Pravilo dopisovanja kaže, da je funkcija opredeljena z R → R, zato je domena niz realnih številk. In co -ooMinium in pot prav tako sovpada z resničnim.

Rešitev c

To je funkcija, s pravilom dopisovanja:

f (x) = x²

Domena in kodominium sta nastavljena v reaisu, vendar je pot sestavljena le iz pozitivnih realnih številk, označena kot r⁺ in vključno z 0.

Rešitev d

Je funkcija. Njegovo dopisovno pravilo je:

f (x) = x/3

Njegova domena je nabor naravnih števil n in kodominija, pa tudi pot so resnične N številke r r.