Značilnosti, enačbe in primeri obveznih pravic

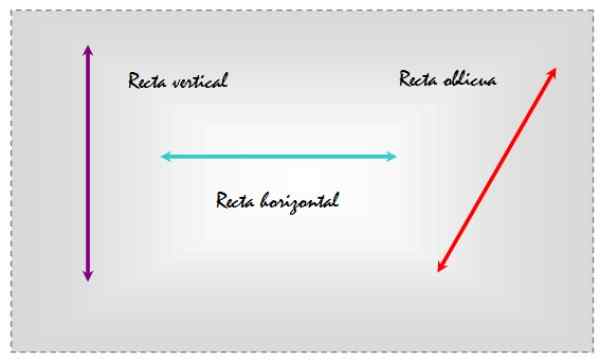
The poševne črte So tisti, ki so nagnjeni, bodisi glede na ravno površino ali drugo črto, ki označuje določen naslov. Kot primer razmislite o treh vrsticah, narisanih v ravnini, ki se pojavijo na naslednji sliki.

Poznamo njihove relativne položaje, ker jih primerjamo z referenčno črto, ki je običajno Os x ki označuje vodoravno.

Slika 1. Navpične, vodoravne in poševne črte v isti ravnini. Vir: f. Zapata.

Na ta način je izbira horizontalne reference leva črta navpična, središče je vodoravno in tisto na desni.

Zdaj črte, ki so na isti ravnini, na primer površina papirja ali zaslon, zavzemajo različne položaje med seboj, odvisno od tega, ali sekajo ali ne. V prvem primeru so suhi naravnost, v drugem pa vzporedni.

Po drugi strani so lahko sušilne črte tudi poševne ali pravokotne ravne črte. V obeh primerih so pobočja črte drugačna, vendar poševne črte med seboj tvorijo α in β kote, razen 90 °, koti, ki jih določajo pravokotne črte, pa so vedno 90 °.

Na naslednji sliki so te definicije povzete:

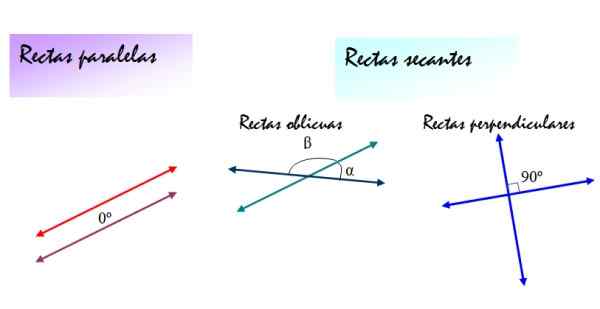Slika 2. Relativni položaji med črtami: vzporedni, poševni in pravokotni se razlikujejo pod kotom, ki se tvori med seboj. Vir: f. Zapata.

[TOC]

Enačbe

Če želite vedeti relativne položaje črte v ravnini, je treba poznati kot, ki ga tvorijo drug z drugim. Upoštevajte, da so vrstice:

Vam lahko služi: izračun pristopov z uporabo diferencialov

Vzporedno: Če imajo enak naklon (enaka smer) in se nikoli ne sekajo, zato so njihove točke enako oddaljene.

Naključja: Ko vse njihove točke sovpadajo in imajo zato enak naklon, vendar je razdalja med njihovimi točkami nič.

Secantes: Če so vaši uhani različni, se razdalja med njihovimi točkami razlikuje in križišče je ena sama točka.

Torej, način vedenja, ali sta dve vrstici v ravnini suhi ali vzporedni, je skozi pobočje. Kriteriji paralelizma in pravokotnosti vrstic so naslednja:

Biti dve vrstici l₁ in l₂ pripada letalu, katerega v čakanju so m₁ in m₂. Te vrstice so vzporedne, če je m₁ = m₂ in so pravokotni, ko m₁= -1/m₂

Če poznamo pobočja dveh vrstic v ravnini, nobeno od zgornjih meril ni izpolnjeno, sklepamo, da so črte poševne. Če poznamo dve točki črte, se naklon izračuna takoj, kot bomo videli v naslednjem razdelku.

Lahko ugotovite, ali sta dve vrstici suhi ali vzporedni, ki najdeta svoje presečišče in rešite sistem enačb, ki se oblikujejo: Če je rešitev, so suhe naključje.

Vendar nas to merilo ne obvešča o kotu med temi črtami, tudi če imajo križišče.

Za poznavanje kota med črtami sta potrebna dva vektorja ali in v ki pripadajo vsakemu od njih. Tako je mogoče vedeti kot, ki ga tvorijo skozi skalarni produkt vektorjev, opredeljen na ta način:

ali•v =ali.v.cos α

Linijska enačba v ravnini

Črta v kartezijanski ravnini je lahko predstavljena na več načinov, kot so:

Lahko vam služi: splošna enačba parabole (primeri in vaje)

-Obrazec za nerešnjo: Ja m Je naklon črte in b To je presečišče črte z navpično osi, enačba črte je y = mx +b.

-Splošna enačba za ravno črto: AX + BY + C = 0, kje M = a/b To je pobočje.

V kartezijanski ravnini so navpične in vodoravne črte posebni primeri enačbe črte.

-Navpične črte: x = a

-Vodoravne črte: y = k

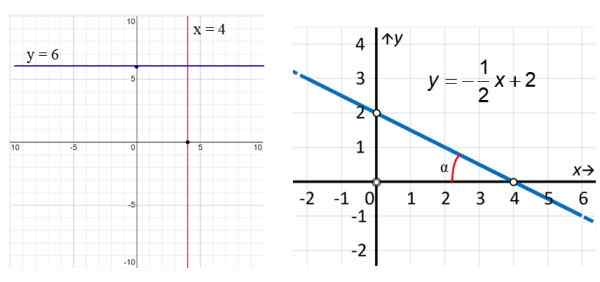Slika 3. Na levi navpični črti x = 4 in vodoravna črta y = 6. Na desni primer poševne črte. Vir: f. Zapata.

V primerih slike 3 ima navpična rdeča črta enačbo x = 4, medtem ko je črta vzporedna z osi x (modra) enačba y = 6. Kar se tiče prave črte, vidimo, da je poševno in da najdemo svojo enačbo, uporabljamo točke, označene na sliki: (0,2) in (4.0) na ta način:

M = (in₂ - in₁) / (X₂ - x₁) = (2 - 0) / (0 - 4) = - ½

Rez te črte z navpično osi je y = 2, Kot je razvidno iz grafike. S temi informacijami:

y = (-½) x+2

Določitev kot naklona glede na osi x je preprosto. Čutim da:

α = ARCTG (2/4) = 26.6

Zato je pozitiven kot od osi x do črte: 180 ° - 26.6. = 153.4

Primeri poševnih linij

Slika 4. Primeri poševnih linij. Vir: Ian Patterson Wrathful [CC by (https: // createCommons.Org/licence/by/2.0)]. Pisin nagnjen stolp. Pixabay.

Poševne linije se pojavljajo na mnogih mestih, zato je pozoren na njihovo iskanje v arhitekturi, športu, ožičenju z električno energijo, cevmi in na mnogih drugih krajih. V naravi so prisotne tudi poševne črte, kot bomo videli spodaj:

Vam lahko služi: pravila izpeljave (s primeri)

Žarki svetlobe

Sončna svetloba se širi v ravni črti, vendar zaobljena oblika zemlje vpliva na način, kako sončna svetloba vpliva.

Na spodnji sliki lahko jasno cenimo, da sončni žarki v tropskih regijah pravokotno vplivajo na pravokotno, namesto tega pa poševno pridejo na površino v zmernih regijah in v polov.

Zato sončni žarki potujejo na daljši razdalji skozi ozračje in tudi toplota se širi na večji površini (glej sliko). Rezultat tega je, da so območja blizu polov hladnejša.

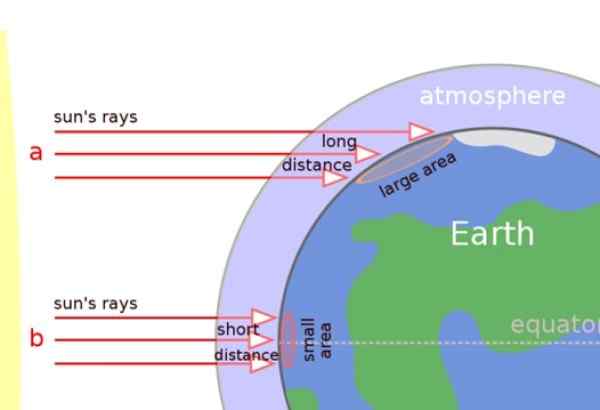Slika 5. Sončni žarki poševno vplivajo na zmerne cone in drogove, vendar so v tropih bolj ali manj pravokotni. Vir: Wikimedia Commons.

Črte, ki niso v isti ravnini

Ko dve vrstici nista v isti ravnini, sta še vedno lahko poševna oz hvaljen, kot so znani tudi. V tem primeru njegovi direktorji niso vzporedni, vendar ne pripadajo isti ravnini, te črte nimajo križišča.

Na primer, črte na pravi sliki so očitno v različnih ravninah. Če pogledajo od zgoraj, opazimo, da učinkovito prečkajo, vendar nimajo skupne točke. Na desni strani vidimo kolesarska kolesa, katerih žarki se zdijo, ko gledajo naravnost naprej.

Slika 6. Poševne črte, ki pripadajo različnim letalom. Vir: levo f. Zapata, desno Pixabay.

Reference

1. Geometrija. Vektorski direktor linije. Okreval od: Juanbragado.je.
2. Larson, r. 2006. Izračun z analitično geometrijo. 8. Izdaja. McGraw Hill.
3. Matematika je igra. Črte in koti. Okreval od: Juntadeandalucia.je.
4. Črte, ki prečkajo. Okrevano od: Teacherttuna.com.
5. Villena, m. Analitična geometrija v R3. Pridobljeno iz: dspace.Espol.Edu.Ec.