Področje rednega in nepravilnega pentagona, kako se sprejme, vaje

Za izračun Območje pentagona Najprej moramo ugotoviti, ali je to redno ali ne. Pentagon je poligon, zaprta ploščata številka petih strani. Ko je poligon reden, to pomeni, da je dolžina strani enaka in tudi njeni notranji koti.

V tem primeru obstaja formula za izračun natančnega območja rednega poligona, ki pozna nekatere njegove glavne značilnosti, za katere bomo sklepali kasneje.

Dva pentagona

Če poligon ni reden, to je, da ima strani različnih velikosti in neenake notranje kote, ni ene same formule.

Vendar so matematiki našli strategije izračuna, kot je delitev številke na druge z najnižjim številom strani, kot so trikotniki, kvadratki in pravokotniki, katerih dimenzije so znane ali enostavno izračunane.

Drug postopek za izračun območij poligonov na splošno, ki pozna koordinate svojih točk, je metoda, imenovana Gaussove determinante, da bomo opisali kasneje.

[TOC]

Kako izračunati območje običajnega pentagona?

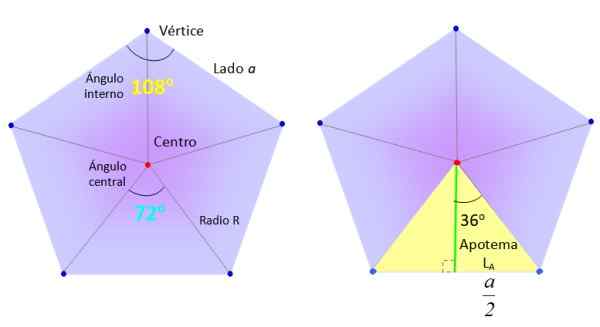
S strani A bomo vzeli navaden pentagon in ga bomo razdelili na 5 enakih trikotnikov, kot je prikazano na sliki, in segmente črpali od središča (rdeče) do vrhov (modra).

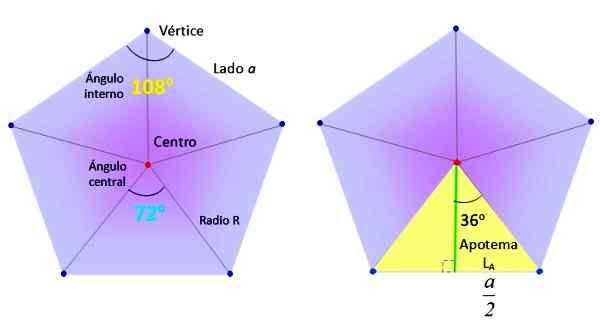Potrebni elementi za iskanje običajnega območja Pentagona. Vir: f. Zapata.

Trikotniki, kot je izjemna rumena na desni strani, so razdeljeni na dva enaka pravokotnika, zahvaljujoč zelenemu segmentu apotem.

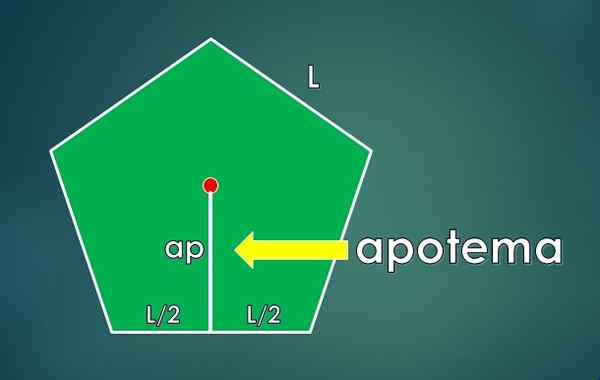
Apotema je opredeljen kot pravokotni segment, ki se povezuje s sredino poligona s sredino ene strani. Njegova dolžina je l_Do.

Območje pravokotnika trikotnika osnovnega a/2 in višine l_Do je:

[(A/2) x l_Do]

Pentagon ima 10 trikotnikov, kot je ta, zato je njegovo območje:

Vam lahko služi: vektorske funkcije

A = 10 (a/2) x l_Do

Toda obod Str pentagona je natančno p =10a, Zato je območje podan s polproduktom oboda in dolžino apotema:

A = p x l_Do /2

Redno območje Pentagona, ki pozna stran a

Izražanje dolžine apotema l_Do Odvisno od strani A, vedoč, da je navedeni kot polovici osrednjega kota, to je 36 °, kar je enakovredno:

36 ° = π/5

Z osnovno trigonometrijo, s tangentom akutnega kota 36 °:

Tan (π/5) = (a/2) ÷ l_Do

Torej:

L_Do=  (A/2) ÷ tan (π/5)

Zamenjava na območju, odštete v prejšnjem razdelku, in vedoč, da je p = 5a:

A = p x l_Do /2

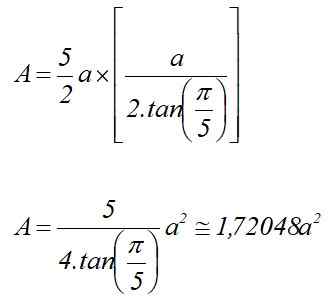
Redno območje Pentagona, ki pozna svoj radio

On radio navadnega poligona je segment, ki sega od središča do ene od njegovih točk. Sovpada s polmerom omejenega oboda, kot je prikazano na naslednji sliki:

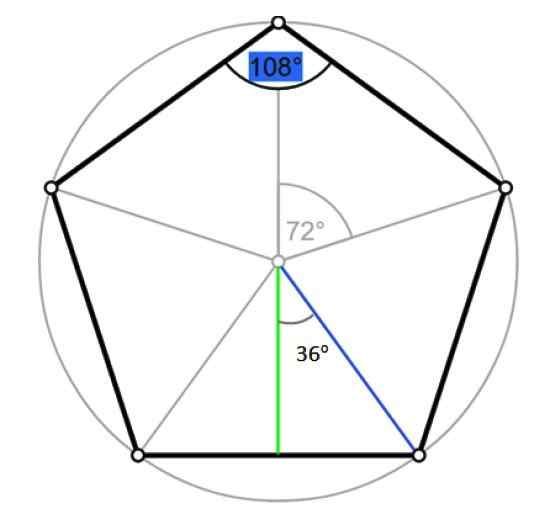Koti in apotem Pentagona. Vir: Wikimedia Commons/F. Zapata.

Naj bo R merilo omenjenega radia, ki sovpada s hipotenuzo desnega trikotnika, ki je bila razmejena na prejšnji sliki, v modri barvi. S trigonometrijo:

cos 36 ° = cos (π/5) = l_Do ÷ r

In

sin 36 ° = sin (π/5) = (a/2) ÷ r

Zato:

A = p x l_Do /2 = 5r. greh (π/5) x r. cos (π/5) = 5r² [sin (π/5) x cos (π/5)]]

Uporaba formule dvojnega kota:

greh (2θ) = 2 sen θ . cos θ

Moramo:

[sin (π/5) x cos (π/5)] = (1/2) sin 72 °

In tako z zamenjavo te vrednosti pridobimo naslednjo formulo za redno območje Pentagona:

A = (5/2) r².Sen 72 °

Kako izračunati območje nepravilnega pentagona?

Kot smo že povedali, za nepravilni poligon ni ene same formule, vendar obstajata dve metodi, ki ponavadi delujeta zelo dobro, prvo se imenuje triangulacija, druga.

Vam lahko služi: Teorem o obstoju in edinstvenosti: demonstracija, primeri in vaje

Triangulacija

Sestavljen je iz delitve figure na trikotnike, katerih območje je lažje izračunati, ali pa ga je mogoče preizkusiti z drugimi številkami, katerih območje je znano, kot so kvadratki, pravokotniki in trapezidi.

Gaussove determinante

Drug način, kako najti nepravilno območje Pentagona ali drugega nepravilnega poligona.

Za izračun območja se uporablja metoda Gaussove determinante, ki jo poznamo, metoda Gaussove determinante, ki je podana z naslednjo formulo:

Kjer je a območje poligona in (x_n , in_n ) so koordinate vrhov. Poligon n strani ima 5 vrhov, za Pentagon bi bil n = 5:

Palice, ki spremljajo formulo, so modulne palice ali absolutna vrednost.

To pomeni, da čeprav je rezultat operacije negativen, ga moramo izraziti s pozitivnim znakom, in če je že pozitiven, ga moramo ostati s tem znakom. To je zato, ker je območje vedno pozitiven znesek.

Postopek imenuje Gaussove determinante s svojim ustvarjalcem, nemškim matematikom Carl F. Gauss (1777-1855). Navedene operacije so enakovredne determinanti matrike 2 × 2, na primer prva determinanta je:

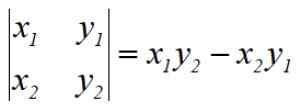
Če želite najti območje Pentagona, moramo rešiti 5 determinantov, dodati rezultat algebraično, ga razdeliti na 2 in končno izraziti območje s pozitivnim znakom.

Rešene vaje

Vaja 1

Poiščite redno območje Pentagona, katerega apotem je vreden 4 cm in katerih stranski meri 5.9 cm.

Rešitev

Ker gre za redni pentagon in imamo mero strani in apotema, uporabljamo formulo, ki je bila prej odšteta:

Vam lahko služi: Scaleno Triangle

A = p x l_Do /2

Obod P je enak 5A = 5 x 5.9 cm = 29.5 cm.

A = 29.5 cm x 4 cm / 2 = 59 cm²

Vaja 2

Poiščite prikazano območje nepravilnega pentagona. Naslednje dimenzije so znane:

Dc ≈ od

Ae = ab = 5

BC = 12

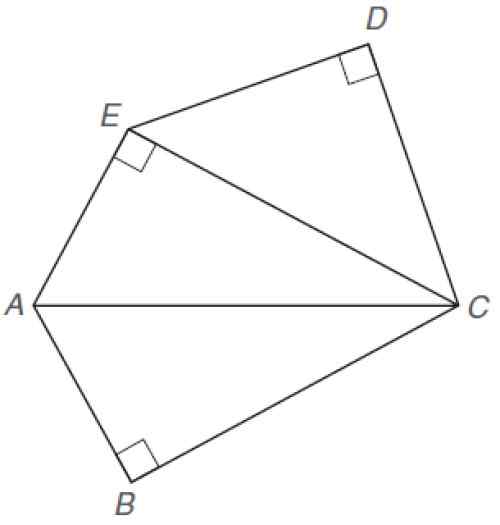Nepravilen pentagon. Vir: Aleksander, D. 2013. Geometrija. 5. Izdaja. Cengage učenje.

Rešitev

Območje Pentagona je vsota območij trikotnikov, ki so pravokotniki. V izjavi piše, da ima DC ≈ od uporabe teorema Pitagore na trikotniku EDC,:

Ec² = 2 ed². Potem ec = √2.Ed.

Trikotniki AEC in ABC imata skupno hipotenuzo, ki je torej izmenični segment:

Ea² + Ec² = Ab² + Pr²

Ker EA in AB merita enako, se pridobi:

Ec = bc = √2.Ed

Ker BC = 12, potem ed = 12 / √2 = 8.485.

S temi vrednostmi bomo izračunali območje vsakega trikotnika in jih dodali na koncu.

Območje EDC Triangle 

Ed x dc /2 = 8.485² / 2 = 36

Območje AEC Triangle 

Ea x ec / 2 = ea x √2.Ed / 2 = 5 x √2. 8.485/2 = 30

ABC območje trikotnika 

AB X BC / 2

Potem je iskanje območja:

5 x 12/2 = 30

Je enako kot pri trikotniku AEC, saj imata oba enake ukrepe.

Nepravilno območje Pentagona

Končno je zahtevano območje vsota območij treh trikotnikov:

A = 36 + 30 + 30 enot = 96 enot.

Reference

1. Aleksander, d. 2013. Geometrija. 5. Izdaja. Cengage učenje.
2. Open Reference Math Open. Območje poligona. Okreval od: Mathpenref.com.
3. Formule vesolja. Območje nepravilnega pentagona. Okrevano od: univerzeformulas.com.
4. Formule vesolja. Območje navadnega pentagona. Okrevano od: univerzeformulas.com.
5. Wikipedija. Pentagon. Okrevano od: je.Wikipedija.com.