Convergence Radio Opredelitev, primeri in vaje rešene

On Konvergenčni polmer niza moči je polmer kroga konvergence, na katerega se serija zbliža. Ta krog sega od vrednosti, ki prekliče osnovo moči do najbližje posebnosti funkcije, povezane s serijo.

Vsa analitična funkcija f (z) Povezala je vrsto moči okoli nesingularne točke, imenovana Serija Taylor:

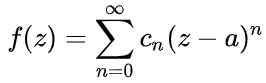
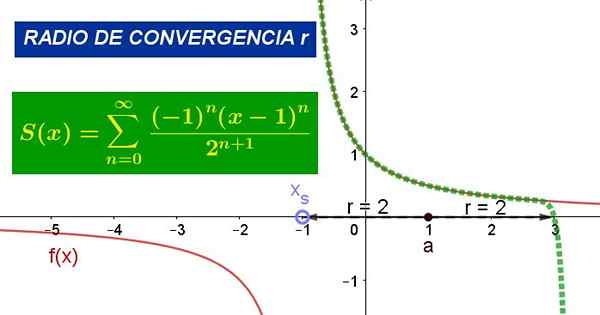
Slika 1. Graf prikazuje serijo moči okoli vrednosti A = 1 za funkcijo f (x). Njegov polmer konvergence je r = 2. Vir: Fanny Zapata.

Kje do Je središče kroga konvergence, z neodvisna spremenljivka funkcije in c_n So koeficienti, povezani s tistimi, ki izhajajo iz funkcije F na točki z = a.

Polmer konvergence r To je pozitivno resnično število, ki definira regijo:

| Z - a | < r

Kjer se serija konvergira. Iz te regije se različni seriji, torej jemljejo neskončne vrednosti. Ko je polmer konvergence neskončen, se serija zbliža v celotni kompleksni ravnini.

[TOC]

Kako je določen polmer konvergence?

Da bi bila serija konvergentna, je potrebno, da se bo absolutna vrednost zaporednih izrazov zmanjšala, ko je število izrazov zelo veliko. Na matematičen način bi bil izražen na naslednji način:

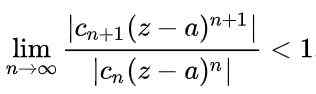
Z uporabo lastnosti mej v prejšnjem izrazu se dobi:

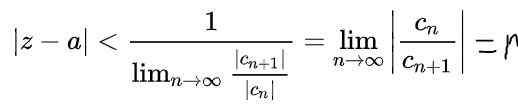
Tukaj r To je polmer konvergence in | Z - a | < r To je odprti obmejni krog v kompleksni ravnini, kjer se serija zbliža. V primeru vrednosti do In spremenljivka Z so realne številke, potem bo odprt interval konvergence na resnični osi: (A - r, a+r).

Serija Taylor

Taylorjeva serija funkcije f (x) Okoli vrednosti do V katerem ima funkcija neskončne derivate, je niz moči, ki je opredeljena kot:

Lahko vam služi: aksiomi verjetnosti: vrste, razlaga, primeri, vaje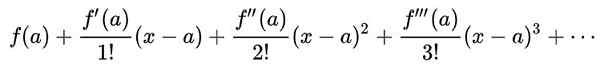

V okolju | X - a | < r, z r kotPolmer konvergence serije, serija Taylor in funkcija morajo biti f (x) Sovpadajo.

Po drugi strani pa polmer konvergence r Je razdalja točke do in singularnost x_s bližje točki do, Singularni točke te vrednosti, kjer se meja funkcije ponavadi na neskončnost.

To je, kdaj x → x_s tako F → ± ∞.

Primeri

Primer 1

Biti S (x) Moči, ki jih daje naslednji izraz:

S (x) = 1 - x + x²- x³+ x⁴-.. .+(-1)ⁿ ⋅ xⁿ +.. .

Za določitev regije, v kateri se serija konvergira, izračunamo količnik med izrazom (n-beeimo + 1) in izrazom (n-eme):

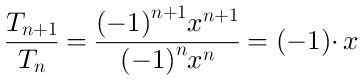
Absolutna vrednost sprednjega količnika je | x | in njegova meja, kdaj N → ∞ je tudi  | x |.

Da se serija konvergentna, je treba:

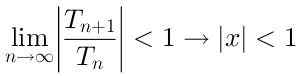
Torej je polmer konvergence te serije R = 1, Ker se zbliža za vrednosti X, ki so na razdalji manj kot 1 glede na center x = 0.

Primer 2

Želite najti serijo funkcije Taylor f (x) = 1 / (1 + x) okoli točke x = 0 in določite njegov polmer konvergence.

Če želite najti serijo, se lotimo zaporednih derivatov funkcije f (x), od katerih bomo prikazali prve tri:

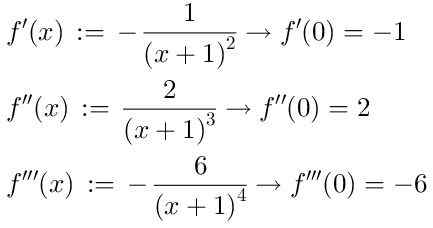
Upoštevajoč, da je izraz ničelnega naročila serije Taylor:

 f (0) = 1,

Prvo naročilo: F '(0)/1!

Drugo vrstni red:

 F "(0)/2!

Tretji naročilo:

 f "(0)/3!

In tako naprej je taylor serija dane funkcije:

f (x) = 1 - x + x² - x³ + x⁴ -.. .+(-1)ⁿ ⋅ xⁿ +.. .

Lahko vam služi: enakostranični trikotnik: značilnosti, lastnosti, formule, območje

Ki sovpada s serijo moči, preučene v primeru 1.

Rekli smo že, da je polmer konvergence serije Taylor razdalja od središča širitve v seriji, kar je v našem primeru vrednost x = 0 Do prve posebnosti funkcije f (x). 

Ker ima naša funkcija posebnost (to je neskončnost) x = -1, Razdalja med vrednostjo -1 in razširitveni center 0 je | -1 - 0 | = 1, Ugotovljeno je, da je polmer konvergence serije Taylor 1.

Ta rezultat v celoti sovpada s tistim, pridobjem v primeru 1 z drugo metodo.

Dejstvo, da je konvergenčna cona serije Taylor odprt interval (-1, 1), pomeni, da funkcija in serija sovpadata v tem intervalu, vendar ne zunaj istega.

To je prikazano na sliki 2, kjer so vzeli 41 izrazov serije Taylor, ki jih je narisala neprekinjena modra črta, medtem ko je prvotna funkcija prikazana na rdeči črti segmentov.

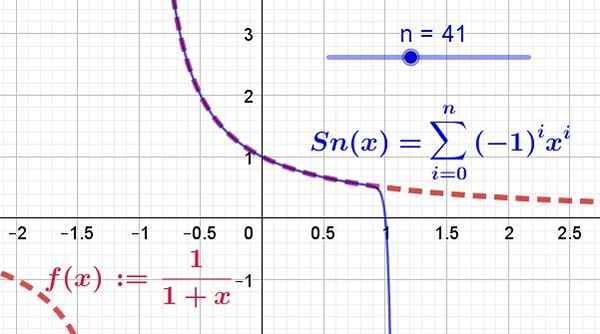Slika 2. Prikazana je funkcija f (x) (v rdeči barvi) in njegova niz moči (ali taylor serija v modri barvi). Lahko ga vidimo kot prvih 41 izrazov serije med -1 in 1. Poleg tega funkcija in njegova serija sovpadata le v konvergenčni regiji. (Vir: Fanny Zapata)

Rešene vaje

- Vaja 1

Razmislite o isti funkciji f (x) = 1 / (1 + x) v primeru 2, vendar tokrat zahteva, da najdete serijo taylor omenjene funkcije okoli točke A = 1.

Rešitev

Najdemo zaporedne izraze serije, začenši z neodvisnim izrazom, ki je f (1) = ½.

Naslednji koeficient, ki ustreza izrazu prvega naročila, je:

F '(1)/1! = -¼

Drugo naročilo je:

f "(1)/2! = 2/(2³ 2!)

Sledite koeficientu tretjega reda:

Lahko vam služi: tetrademágon

f "(1)/3! = -6 / (2⁴ 3!)

In tako naprej. Serija Taylor bo:

Sf (x) = ½ - 1/2² (X-1) + 1/2³(X-1)² - 1/2⁴ (X-1)³ + 1/2⁵ (X-1)⁴-..

- Vaja 2

Poiščite polmer konvergence prejšnje serije

Rešitev

Zapišemo izraz N-EME in izraz N-ALKAUS več:

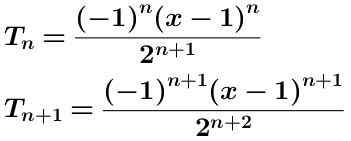Izračunamo količnik teh dveh izrazov, ki je prikazan spodaj poenostavljen:

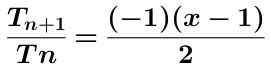
Absolutna vrednost prejšnjega izraza se vzame s pridobitvijo:

| X - 1 | / 2

Vendar pa je za konvergentno serijo potrebno, da je prejšnji znesek strogo nižji od enote, to je:

| X - 1 | < 2

Kar kaže, da je polmer konvergence okoli vrednosti x = 1:

R = 1

Po drugi strani je prejšnji izraz enakovreden dvojni neenakosti:

-2 < x - 1 < +2

Če v vsakega od treh članov prejšnjega izraza dodamo +1, ga dobimo:

-1 < x < 3

Kar je interval konvergence serije.

Slika 1 prikazuje izvirno funkcijo in taylor serijo omenjene funkcije okoli točke x = 1. Na sliki je mogoče preveriti, ali serija sovpada s funkcijo v okolju točke x = 1, vendar znotraj polmera konvergence.

Reference

1. Fundacija CK-12. Serija moči: predstavitev funkcij in operacij. Okreval od: CK12.org.
2. Engler, a. 2019. Integralni računanje. Nacionalna univerza na obali.
3. Larson, r. 2010. Izračun spremenljivke. 9na. Izdaja. McGraw Hill.
4. Brezplačna besedila matematike. Serija moči. Okrevano od: matematika.LiibreTexts.org.
5. Wikipedija. Serija moči. Okrevano od: je.Wikipedija.org.
6. Wikipedija. Polmer konvergence. Pridobljeno iz: v.Wikipedija.org