Kaj so notranji nadomestni koti? (Z vajami)

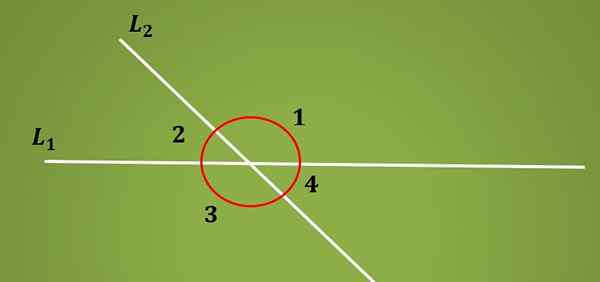
The Notranji nadomestni koti So ti koti, ki jih tvori preseči dve vzporedni črti in prečna črta. Ko se linijo L1 razrežejo s prečno črto L2 4, se oblikujejo.

Dva para kotov, ki ostaneta na isti strani črte L1, se imenujeta dopolnilni koti, saj je njegova vsota enaka 180 °. Na spodnji sliki sta kota 1 in 2 dopolnita, pa tudi kota 3 in 4.

Da bi lahko govorili o notranjih nadomestnih kotih, je treba imeti dve vzporedni črti in prečno črto; Kot je bilo že prej, se bo oblikovalo osem kotov.

Ko obstajata dve vzporedni črti L1 in L2, razrezani s prečno črto, se oblikuje osem kotov, kot je prikazano na naslednji sliki.

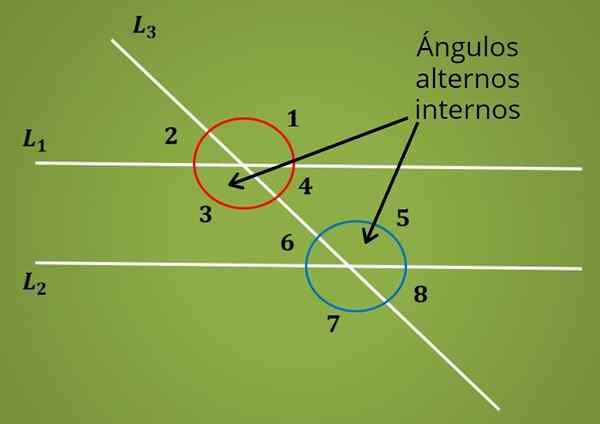
Na vrhunski sliki so pari kotov 1 in 2, 3 in 4, 5 in 6, 7 in 8 dopolnilni koti. 

Zdaj so notranji nadomestni koti tisti med dvema vzporednima črtama L1 in L2, vendar se nahajata na nasprotnih straneh prečne črte L2. To je Kota 3 in 5 sta notranja nadomestna. Podobno sta kota 4 in 6 notranji nadomestni koti.

Nasproti kotov z vrhom

Če želite vedeti uporabnost, ki jo imajo notranji nadomestni koti, je treba najprej vedeti, da če to vrha nasprotujeta dva kota, potem ta dva kota merita isto.

Na primer, kota 1 in 3 merita enako, kot ji nasprotujeta Vertex. Po istem sklepu je mogoče sklepati, da kota 2 in 4, 5 in 7, 6 in 8 merijo isto.

Koti, ki se tvorijo med secantom in dvema vzporednicama

Ko obstajata dve vzporedni črti, ki jih razrežemo s suho ali prečno črto kot na prejšnji sliki, je res, da kota 1 in 5, 2 in 6, 3 in 7, 4 in 8 merijo isto.

Notranji nadomestni koti

Z uporabo definicije kotov, ki jih postavljata vrha, in lastnost kotov, ki nastanejo med sekantom in dvema vzporednima črtama, je mogoče sklepati, da imajo notranji nadomestni koti enak ukrep.

Rešene vaje

- Prva vaja

Izračunajte merilo kota 6 naslednje slike, vedoč, da kot 1 meri 125 °.

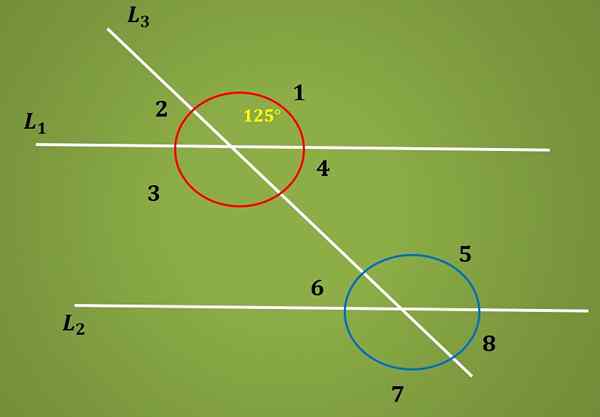
Rešitev

Ker sta kota 1 in 5 nasprotna z vrhom, imate ta kot 3 meri 125 °. Zdaj, ker sta kota 3 in 5 notranja nadomestna, imate ta kot 5 tudi 125 °.

Nazadnje, ker sta kota 5 in 6 dopolnila, je potrebno merilo kota 6 enaka 180 ° - 125 ° = 55 °.

- Druga vaja

Izračunajte kot 3, vedoč, da kot 6 meri 35 °.

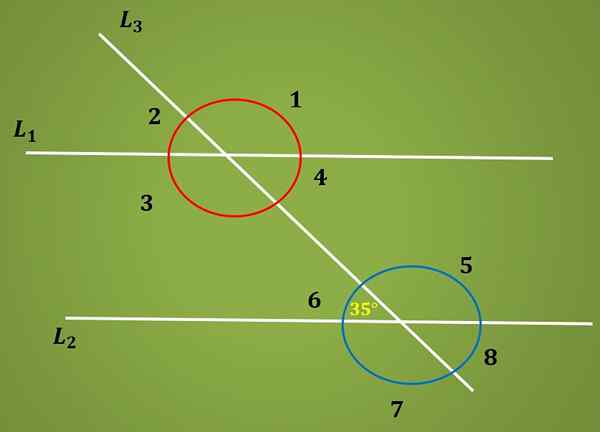
Rešitev

Znano je, da kot 6 meri 35 °, znano pa je tudi, da sta kota 6 in 4 notranji nadomestni, zato merita enako. To pomeni, da kot 4 meri 35 °.

Po drugi strani pa je z dejstvom, da sta kota 4 in 3 dopolnila, merilo kota 3 enaka 180 ° - 35 ° = 145 °.

Opazovanje

Potrebno je, da so črte vzporedne, da lahko izpolnijo ustrezne lastnosti.

Vaje se lahko rešijo hitreje, vendar je ta članek želel uporabiti lastnost notranjih nadomestnih kotov.

Reference

1. Bourke. (2007). Kot na matematični delovni zvezek geometrije. Newpath Learning.
2. Clemens, s. R., O'Dafer, str. G., & Cooney, t. J. (1998). Geometrija. Pearson Education.
3. Lang, s., & Murrow, g. (1988). Geometrija: tečaj srednje šole. Springer Science & Business Media.
4. Lira, a., Jaime, str., Chavez, m., Gallegos, m., & Rodríguez, c. (2006). Geometrija in trigonometrija. Umbral Edition.
5. Moyano, a. R., Saro, a. R., & Ruiz, r. M. (2007). Algebra in kvadratna geometrija. Netbiblo.
6. Sullivan, m. (1997). Trigonometrija in analitična geometrija. Pearson Education.
7. Wingard-Enelson, r. (2012). Geometrija. ENLOW Publishers, Inc.