Kaj je dinamično ravnovesje? (S primerom)

On dinamično ravnovesje To je stanje, v katerem je mobilni objekt v idealnem primeru predstavljen kot delček, ko je njegovo gibanje enakomerno pravokotno. Ta pojav se pojavi, ko je vsota zunanjih sil, ki delujejo nanj.

Običajno se verjame, da če ni nobene mreže ali posledične sile na predmet, je počitek edina možna posledica. Ali tudi, da za telo v ravnovesju ne bi smelo biti nobene sile.

Slika 1. Ta mačka se premika v dinamičnem ravnovesju, če to počne s konstantno hitrostjo. Vir: Pixabay.

Pravzaprav je ravnovesje odsotnost pospeška, zato je konstantna hitrost popolnoma možna. Mačka na sliki se lahko premika brez pospeška.

Predmet, ki ima enotno krožno gibanje, ni v dinamičnem ravnovesju. Čeprav je njegova hitrost konstantna, je proti središču oboda usmerjen pospešek, ki ga ohranja v poti. Ta pospešek je odgovoren za pravilno spreminjanje hitrostni vektor.

Ničelna hitrost je posebna situacija ravnotežja delca, kar je enakovredno pritrditvi, da je predmet v mirovanju.

Kar zadeva obravnavanje predmetov kot delca, je zelo uporabna idealizacija pri opisovanju njihovega globalnega gibanja. Pravzaprav so mobilni predmeti, ki nas obkrožajo, sestavljeni iz velikega števila delcev, katerih posamezna študija bi bila okorna.

[TOC]

Načelo superpozicije

To načelo omogoča nadomeščanje delovanja več sil na objektu z ekvivalentom, imenovanim nastali sili mraz ali neto silo fn in da je v tem primeru nično:

F1 +f2 +f3 +… . = Fr = 0

Kjer sile F1, F2, F3 .. ., Fi so različne sile, ki delujejo na telo. Sumory zapis je kompakten način izražanja:

Dokler neuravnotežena sila ne posreduje, se lahko objekt ohrani v nedogled premika s konstantno hitrostjo, saj lahko to panoramo spremeni le sila.

Glede na sestavne dele nastale sile je dinamični ravnotežni pogoj delca izraženo na naslednji način: fx = 0; Fy = 0; Fz = 0.

Pogoji vrtenja in ravnotežja

Za model delcev je pogoj FR = 0 zadostna garancija za ravnotežje. Vendar pri upoštevanju dimenzij preučevanja mobilnega telefona obstaja možnost, da se objekt vrti.

Rotacijsko gibanje pomeni obstoj pospeška, zato vrtljiva telesa niso v dinamičnem ravnovesju. Obrat telesa ne potrebuje samo sodelovanja sile, ampak je treba uporabiti priročno spletno mesto.

Če želite preveriti, lahko na površino brez trenja postavite tanko palico dolžine, na primer ledeno površino ali zelo polirano ogledalo ali steklo. Običajna stanja do teže navpično in pri uporabi dveh sil F1 in F2 enake velikosti, v skladu s diagramom naslednje slike, kaj se zgodi:

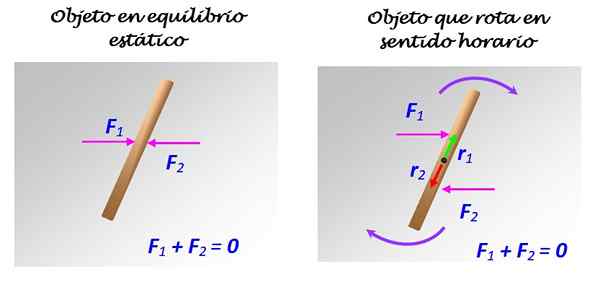Slika 2. Palica na površini brez trenja je lahko ali ne bo v ravnovesju, odvisno od tega, kako se nanašajo sili 1 in 2. Vir: Self Made.

Če se F1 in F2 uporabljata, kot je prikazano na levi strani, s skupno linijo delovanja, bo palica ostala v mirovanju. Če pa se uporabljata F1 in F2, kot je prikazano na desni strani, z različnimi linijami delovanja, čeprav vzporedno, se vrtenje pojavi v urniku, okoli osi, ki poteka skozi sredino.

V tem primeru F1 in F2 predstavljata nekaj sil ali preprosto par.

Navor ali trenutek sile

Učinek navora je ustvariti vrtenje na razširjeni objekt, kot je primer palice. Vektorska velikost se imenuje navora ali tudi trenutek sile. Označen je kot τ in se izračuna z:

τ = r x f

V tem izrazu F je uporabljena sila in r je vektor, ki sega od osi vrtenja do točke uporabe sile (glej sliko 2). Smer τ je vedno pravokotna na ravnino, kjer sta f in r in njene enote v mednarodnem sistemu n.m.

Za primer je smer trenutkov, ki sta jih ustvarila F1 in F2, proti papirju, v skladu s pravili vektorskega izdelka.

Čeprav sile medsebojno prekličejo, njihovi navori ne. Rezultat je prikazana rotacija.

Ravnotežni pogoji za podaljšani predmet

To sta dva pogoja, ki morata biti izpolnjena, da bi zagotovila ravnovesje razširjenega predmeta:

Rešen primer

Imate predal ali prtljažnik, ki tehta 16 kg-f, ki drsi skozi nagnjeno ravnino s konstantno hitrostjo. Kot naklon klina je θ = 36 °. Odgovor:

a) Kakšna je velikost dinamične sile trenja, potrebna za drsenje s konstantno hitrostjo?

b) koliko je koeficient kinetičnega trenja?

c) Če je višina H nagnjene ravnine 3 metre, poiščite hitrost spuščanja prtljažnika, vedoč, da traja 4 sekunde, da pridete do tal.

Rešitev

Deblo lahko obdelamo, kot da bi bil delček. Zato bodo sile veljale na točki, ki se nahaja približno v svojem središču, na kateri je mogoče domnevati vso njegovo maso. Do tega trenutka bo sledila skladba.

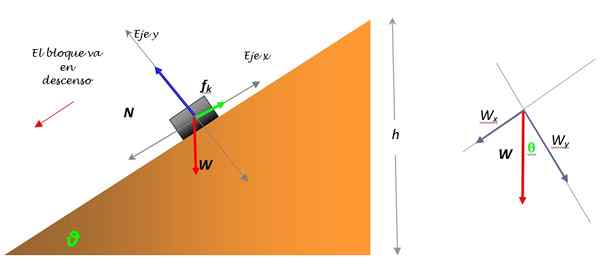Slika 3. Prosti karoserijski diagram za prtljažnik, ki zdrsne navzdol, in razpadanje teže (desno). Vir: Self Made.

Teža W je edina sila, ki ne pade na eno od koordinatnih osi in jo je treba razčleniti na dve komponenti: WX in WY. Ta razgradnja je prikazana v shemi (slika 3).

Prav tako je priročno prenesti težo na enote mednarodnega sistema, za katere je dovolj, da se pomnoži z 9.8:

Wy = w.cosθ = 16 x 9.8 x cos 36º n = 126.9 n

Wx = w.Senθ = 16 x 9.8 x greh 36 ° = 92.2 n

Oddelek a

V celotni vodoravni osi so vodoravna komponenta teže WX in FK dinamično ali kinetično trenje, ki nasprotuje gibanju.

Če izberete pozitiven smisel v smeri gibanja, je enostavno opaziti, da je WX odgovoren za to, da se blok spusti navzdol. In ker trenje nasprotuje, namesto da bi hitro zdrsnilo, ima blok možnost, da nenehno drsi navzdol.

Prvo ravnotežno stanje zadostuje, saj deblo obravnavamo kot delček, kar je zagotovljeno v izjavi, ki je v dinamičnem ravnovesju:

Wx - fk = 0 (v vodoravnem naslovu ni pospeška)

Fk = 92.2 n

Oddelek b

Obseg dinamičnega trenja je konstantna in jo daje fk = μk n. To pomeni, da je dinamična sila trenja sorazmerna z normalno in velikost tega je potrebna za spoznavanje koeficienta trenja.

Opazovanje prostega telesnega diagrama je razvidno, da imamo na navpični osi normalno silo n, ki jo klin izvaja na prtljažniku in je usmerjen navzgor. Je uravnotežena z navpično komponento teže. Izbira kot pozitiven smisel in uporaba Newtonovega drugega zakona in rezultatov stanja ravnotežja:

N - wy = 0 (vzdolž navpične osi ni gibanja)

Zato:

N = wy = 126.9 n

fk = μk n

μK = fk / n = 92.2 /126.9 = 0.73

Oddelek c

Trigonometrija najde skupno razdaljo, ki jo prevozi deblo od vrha klina do tal:

d = h/sin 36 ° = 3/greh 36 ° M = 5.1 m.

Za izračun hitrosti se uporablja definicija za enotno pravokotno gibanje:

V = d/t = 5.1 m/4 s = 1.3 m/s

Reference

1. Rex, a. 2011. Osnove fizike. Pearson. 76 - 90.
2. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7. Ed. Cengage učenje. 120 - 124.
3. Serway, r., Vulle, c. 2011. Osnove fizike. 9na ed. Cengage učenje. 99-112.
4. Tippens, str. 2011. Fizika: pojmi in aplikacije. 7. izdaja. MacGraw Hill. 71 - 87.
5. Walker, J. 2010. Fizika. Addison Wesley. 148-164.