Radikalne lastnosti

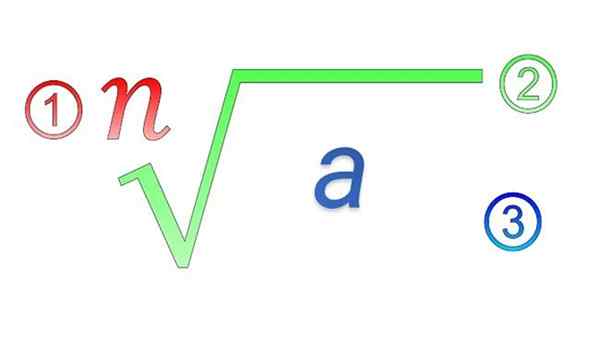
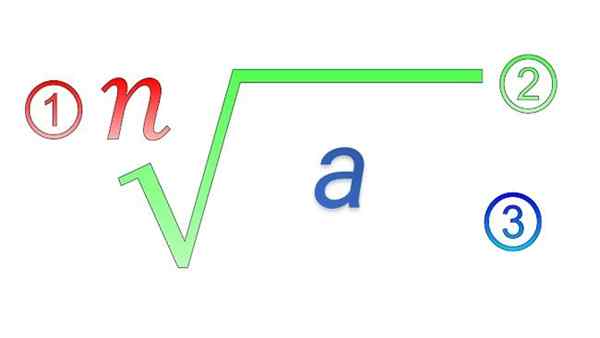Radikalni elementi: 1) indeks; 2) radikalni simbol; 3) Subradikalna količina

Kakšne so lastnosti radikalov?

The radikalne lastnosti Gre za operacije, ki omogočajo reševanje zapletenih problemov radikalov in moči. Radikal je način, kako matematično simbolizirati N-EM-om zneska "A". Ta koren je še en znesek, imenovan "B", tako da je njegovo ime natančno "A", zato je veljavno napisati naslednje:

Vrednost "n" je naravno število, ki je znano kot koreninski indeks " Radikalno ali subradikalna količina in "B" je N-EME "A" koren. Tako "a" kot "b" pripadata naboru resničnih številk.

Če indeks ni napisan v radikalu, se takoj razume, da je njegova vrednost enaka 2 in bere "kvadratni koren a".

Ker "N" pripada naboru naravnih številk, je lahko par ali lih številka. Nato se razlikujejo naslednji primeri:

Za "n" par

• Če je a> 0 ali enako 0, je n-alkalni koren "a" pozitiven ali 0 in se imenuje Glavni koren.
• Kdaj < 0, no existe raíz n-ésima en el conjunto de los números reales, pero sí en los números complejos.

Za "N" Odd

• Da a> 0, n-eme korenine "a" je pozitiven.
• Kdaj< 0, la raíz n-ésima de “a” es negativa.

Nekaj ​​primerov je naslednje:

Snemalne lastnosti

Možno je napisati ime zneska zneska kot moč z delnim eksponentom, to je racionalno število.

V tem primeru koreninski indeks postane imenovalec, medtem ko eksponent subradične količine postane števca:

Vam lahko služi: homografska funkcija: kako graditi, rešiti vaje

Izraz, ki je veljaven, dokler je n ≠ 0, saj ni sprejeti nobenih frakcij z imenovalcem.

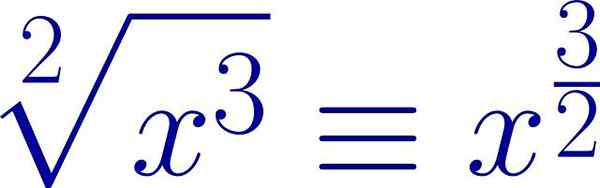Primer radikalnega izraza, zapisanega v obliki frakcijskega eksponent. Koren indeks je imenovalec eksponenta, medtem ko je moč oddaje števca. Vir: Wikimedia Commons.

Na ta način je mogoče v primeru radikalov uporabiti iste lastnosti, ki veljajo za pooblastila.

Za vrednosti, ki pripadajo naboru resničnih števil, so te lastnosti naslednje:

1. Radikalni produkt enakega indeksa

V produktu dveh (ali več) radikalov istega indeksa se pomnožene subradične količine pomnožijo in vzdržujejo indeks:

2. Radikalni količnik istega indeksa

Quostient med n-korencem "A" in n-eme "b", ki je b ≠ 0, je enak N-emeasy korenini količni med "A" in "B":

3. Koreninski koren

Če želite najti n-odmevno korenino m-eme zneska "a", je subradični znesek zapisan pod korenino, katerega indeks je izdelek med "n" in "m":

Postopek se zlahka razširi na zaporedne ugnezdene korenine. Nastali koreninski indeks je produkt vseh indeksov, kot je ta:

4. Korenska moč

N-THO, dvignjen na moč M, izraža subradični znesek omenjene moči:

Posebni primeri:

1) Da n = m, Koren znak izgine, pri čemer je podlago dvignjeno na moč 1:

Ki velja za ≥ 0. Na splošno, če je korenski indeks enakomerna številka, imate:

(Glej primere kasneje)

2) Da m> n, Frakcija M/N je neprimerna in koren je mogoče poenostaviti, na primer, iščejo frakcijo, enakovredno M/N Tu opisane lastnosti.

Vam lahko služi: prizme in piramide

(Glej primere kasneje)

5. Radikalna amplifikacija

Radikal lahko ojača s faktorjem q, Če tako koreninski indeks, kot tudi moč subratdikalne količine, se pomnožite z omenjenim faktorjem in ta operacija ne pomeni spreminjanja rezultata. Zato:

Pod pogojem, da je ≥ 0, ko je celo.

6. Uvedba faktorja znotraj radikala

Če pozitiven faktor "B" pomnoži radikal, lahko preide v njega, če se dvigne na isti koreninski indeks. V tem primeru:

7. Vsota in odštevanje radikalov

Radikali lahko dodajo in odštejejo, če so isti indeks in imajo enako subradično količino.

Ko sta dva ali več radikalnih enakih indeksov in subradikalne količine, se reče, da sta Podobni radikali.

Na primer, naslednji radikali so podobni:

Namesto tega ti radikali niso podobni, ker nimajo enake subradične zneske:

Prav tako nista ta dva podobna:

Ker radikalni indeks ni enak.

Podobne radikale je mogoče zmanjšati na enega in dodati ali odštevati koeficiente, ki jih spremljajo.

Primeri radikalnih lastnosti

Primer 1

Kakšna je vrednost naslednjih korenin?

Kvadratni koren 32 najdete neposredno s pomočjo kalkulatorja. Njegova vrednost je:

Točke suspenzije kažejo, da obstajajo neskončne decimalne.

Če raje ne delate z decimalnimi številkami, lahko kvadratni koren 32 izračunamo tudi tako, da se razgradi 32 v njegovih glavnih dejavnikih:

32 = 2⁵

Na ta način se pri zamenjavi dobi:

Vam lahko služi: delitve 8: Kaj so in lahka razlaga

Napisan kot delni eksponent:

Frakcija 5/2 je neprimerna, zato je mogoče radikal poenostaviti z lastnosti pooblastil:

Zdaj uporaba nepremičnine 1 zgoraj:

Zato:

S svojim delom:

Ker (−2)³ = −8.

Po premoženju 4:

In končno, kvadratni koren −8 ne obstaja v naboru realnih števil, čeprav v zapletenih številkah.

Primer 2

Glede na naslednjo operacijo:

Ali je mogoče zmanjšati rezultat?

Pod pogojem, da so radikali podobni, jih je mogoče zmanjšati, vendar morajo imeti za to enak indeks in isto subradično količino. V prejšnjem primeru je bilo videti:

Za pisanje prvega dodajanja se lahko uporabi analogen postopek, tako da je subradični znesek enak 2:

Ta radikal je podoben prejšnjemu. Kar zadeva kvadratni koren 81, je torej 9:

Primer 3

Katere lastnosti so potrebne za izvedbo te operacije?

Uporabiti moramo lastnosti 3 in 5, ki sta koren korenine in vnos korenine vrednosti. Najprej velja lastnina 5, da uvede "X", ki je zunaj notranjega korena:

In zdaj je izraz pripravljen za uporabo lastnosti 3 in pomnožiti ustrezne indekse vsakega radikala:

Reference

1. Gonzales, d. 2011. Osnovna algebra: teorija in praksa. 2. mesto. Izdaja.
2. Haeussler, npr. 2012. Prekalenkulacija. 1. Izdaja. Pearson.
3. Khan AcadAem. Eksponenti in radikali. Okreval od: Khanacademy.org.
4. Larson, r. 2012. Prekalenkulacija. 8. Izdaja. Cengage učenje.
5. Stewart, J. 2007. Matematika za izračun. 5. Izdaja. Cengage učenje.