Omejitve lastnosti (s primeri)

The Omejitve lastnosti So nabor algebrskih pravil in postopkov, ki se uporabljajo za njihovo določanje. Koncept meje je bistven za izračun in iskanje njene vrednosti ne sme biti zapletena naloga, če se njegove lastnosti z lahkoto ravna.

Spodaj je seznam najpomembnejših, ki ga spremljajo primeri prijave.

Omejitve in njegove lastnosti so osnova izračuna. Na sliki je prikazana zelo posebna meja: derivat funkcije f (x)

Naj B, C, N, A in B realne številke in F in g Takšne funkcije, ki preverjajo naslednje:

Potem imate naslednje lastnosti:

1. Neposredna omejitev zamenjave

V prvi stopnji lahko mejo funkcije f, ko lahko x → c izračunamo neposredno nadomestitev x = c v funkciji. Če funkcija obstaja pri x = c, potem je meja:

Vendar ni nujno, da mora biti funkcija definirana pri x = c, tako da meja obstaja. Ideja je, da se približate toliko, kot želite do vrednosti x = c in videti, kaj se v tem primeru zgodi s funkcijo.

Primer

Poiščite mejo f (x) = x² Ko x → 4

Rešitev

Omejitev rešuje preprosto z zamenjavo x = 4 v f (x) = x², Ker pri izvajanju operacije ni neprijetnosti:

2. Edinstvenost meje

Če je meja funkcije f (x), ko obstaja X → C in je vreden L, je omenjena meja edinstvena.

Zato so stranske meje, ki so tiste, ko je x → c^- (Preberite "X se nagiba na C z leve") in ko x → C⁺ (Bere se "x se nagiba k c na desni"), oba obstajata in imata enako vrednost L, tudi če funkcija ni določena v x = c.

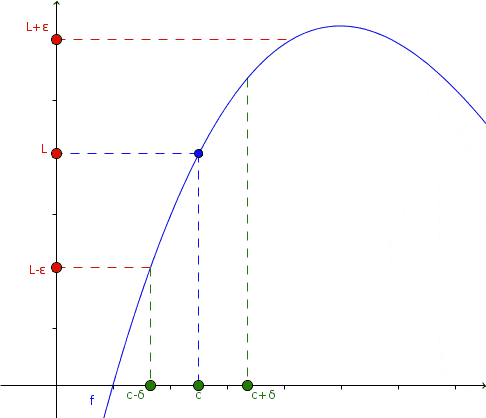V tej animaciji je predstavljen koncept meje: ko se x nagiba k določeni vrednosti c, ki se približa tako na levi kot na desni, se vrednost funkcije nagiba k l. Ni nujno, da je funkcija definirana v x = c. Vir: Wikimedia Commons.

V animaciji je ta pristop opažen in kaj se zgodi s funkcijo v tem primeru: ali se bliža na levi in ​​desno do x = c, je vrednost funkcije blizu l.

Vam lahko služi: minimalni kvadratki

Matematično izraža tako:

Bočne omejitve omogočajo vedeti, kdaj meja ali ne, ker če ne obstajajo ali če se razlikujejo, je gotovo, da meja funkcije, ko X → C ne obstaja.

Primer

Izračunajte mejo F (x), ko je x → 1, če obstaja, kjer je F (x) podan z:

Rešitev

To je funkcija po delih ali definiranih na koščke, ki je sestavljena iz vrstice 4 -x za vrednosti x < 1 y en la parábola 4 - x² Ko je x enak 1 ali večji od 1.

Z leve strani se lahko približamo x = 1, v tem primeru je del funkcije, ki velja za X<1:

Ker so stranske meje enake, sledi, da meja funkcije, ko obstaja X → 1, in je vredna 3.

3. Stalnica

Omejitev konstante je vrednost omenjene konstante, ne glede na vrednost, na katero se spremenljivka nagiba:

Primer

Izračunati:

Rešitev 

4. Omejitev funkcije identitete

Če je f (x) = x, se vedno izpolni:

Primer

Izračunati:

Rešitev 

5. Omejitev izdelka konstante s funkcijo

V tem primeru konstanta izhaja iz meje in se premakne, da jo pomnoži, kot je ta:

Primer 

Izračunajte, če obstaja, naslednja meja:

Rešitev

Konstanta 5 se zunaj pomnoži do meje in uporabi se nadomestna lastnost:

6. Omejitev vsote

Meja vsote dveh funkcij F in g To je vsota meja:

Primer 

Poiščite naslednjo mejo, če obstaja:

Vam lahko služi: teorija nastavitve: značilnosti, elementi, primeri, vaje

Rešitev

Lastnost vsote meja se najprej uporablja in nato z neposredno zamenjavo, saj operacije ne predstavljajo težav:

 7. Omejitev odštevanja

V primeru meje odštevanja dveh funkcij nadaljujte na analogni način, da je za vsoto: meja odštevanja je odštevanje mej:

Primer

Izračunajte naslednjo mejo:

Rešitev 

Uporabljena je lastnost meje odštevanja dveh funkcij in nato neposredna zamenjava, saj je mogoče vse operacije izvajati brez težav:

8. Omejitev izdelka

Omejitev izdelka dveh funkcij F in g To je izdelek omejitev:

Primer

Izračunajte to mejo:

Rešitev

9. Razmerje količnika

Meja razmerja dveh funkcij F in g To je količnik meja, pod pogojem, da je meja G (x), kadar je x → c drugačna od 0, saj delitev z 0 ni definirana. Tako:

Primer

Izračunajte, če obstaja, vrednost naslednje meje:

Rešitev

Najprej se uporablja lastnost omejitve lastnosti, da pridobi količnik omejitev:

Za iskanje vsake meje se zdaj uporablja nadomestna lastnost:

In ker je B ≠ 0, je iskana meja količina A/B:

10. Omejitev

Omejitev moči eksponenta N je enakovredna meji, ki je bila dvignjena na omenjeno moč, kot sledi:

Primer 1: Omejitev moči X

Če imate na primer mejo moči X, rezultati:

V skladu s premoženjem 4 je ta omejitev:

Vam lahko služi: numerične analogije: vrste, aplikacije in vaje

Primer 2: Koreninska meja

N-ta koren je mogoče zapisati v obliki frakcijskega eksponenta, torej:

Pomembno: Če je koreninski indeks enakomeren, je potrebno, da je meja f (x), kadar je x → c večja ali enaka 0, saj ni resničnih parov negativnih količin.

Primeri

Določite, uporabite prejšnje lastnosti, naslednje omejitve, če obstajajo:

Rešitev

Z lastnino meje pooblastila in neposredne zamenjave je pridobljeno:

Rešitev b

enajst. Omejitev

Če želite najti mejo osnovnega eksponentnega B in eksponenta F (x), je treba osnovo funkcije F (x) dvigniti na naslednji način:

Primer

Poiščite, če obstaja naslednja meja:

Rešitev 

V tej meji je osnova številka E in funkcija f (x) = x², Zato morate najprej izračunati mejo x²  Ko se x nagiba k 1:

Nato se uporabi lastnost eksponentne meje:

12. Omejitev eksponentne potencialne funkcije

Omejitev, ko je x → C funkcije f (x), ki je posledično povišana na drugo funkcijo g (x), izražena z:

Primer

Izračunajte naslednjo mejo, če obstaja:

Rešitev

Za uporabo prejšnje lastnosti so najprej identificirani f (x) = x-1 in g (x) = 2x, nato pa se izračunajo ustrezne meje:

 Končno:

Reference 

1. Ayres, f. 2000. Izračun. 5ed. MC Graw Hill.
2. Leithold, l. 1992. Izračun z analitično geometrijo. Harla, s.Do.
3. Brezplačna besedila matematike. Omejitve. Okrevano od: matematika.LiibreTexts.org.
4. Matematika. Zakoni in omejitve lastnosti. Okreval od: matemovil.com.
5. Larson, r. 2010. Izračun spremenljivke. 9na. Izdaja. McGraw Hill.
6. Purcell, e. J., Varberg, d., & Rigdon, s. In. (2007). Izračun. Mehika: Pearson Education.
7. Formule vesolja. Omejitve lastnosti. Okrevano od: univerzeformulas.com