Nepremičnina Proof, primeri

The Lastnost zaklepanja algebra To je pojav, ki povezuje dva elementa niza z operacijo, kjer je potreben pogoj, da po dveh elementih, ki so pod omenjenim delovanjem, rezultat pripada tudi začetnemu nizu.

Na primer, če se celo številke vzamejo kot celota in vsota kot operacija, dobimo ključavnico omenjenega nabora glede na vsoto. To je zato, ker bo vsota dveh enakomernih številk vedno dana kot rezultat druge številke, s čimer izpolnite pogoj zaklepanja.

Vir: Unpash.com

[TOC]

Značilnosti

Obstaja veliko lastnosti, ki določajo algebrske prostore ali telesa, na primer strukture ali obroči. Vendar je lastnost Lock ena najbolj znanih v osnovni algebri.

Niso vse aplikacije teh lastnosti temeljile na pojavih ali numeričnih elementih. Številni vsakdanji primeri lahko delujejo od algebrskega-teoretičnega pristopa čistega.

Primer so lahko državljani države, ki med drugim prevzame pravni odnos, na primer komercialna ali poročna družba. Po tej operaciji ali upravljanju so še vedno državljani države. Tako državljanstvo in upravljanje v zvezi z dvema državljanom predstavljajo ključavnico.

Numerična algebra

Glede na številke obstaja veliko vidikov, ki so bili razlog za študij v različnih tokovih matematike in algebre. Iz teh študij se je pojavilo veliko aksiomov in teoremov, ki služijo kot teoretična osnova sodobnih raziskav in del.

Če delate s številčnimi nizi, lahko vzpostavimo še eno veljavno definicijo za lastnost zaklepanja. Govori se, da je en sklop A ključavnica drugega kompleta B, če je A najmanjši komplet, ki vsebuje vse sklope in operacije, v katerih je hiša B.

Vam lahko služi: distribucijska lastnina

Demonstracija

Zaklepna demonstracija se uporablja za elemente in operacije, ki so prisotni v naboru resničnih N številk.

Naj bo A in B dve številki, ki pripadata nastavitvi R, zaklepanje teh elementov je opredeljeno za vsako operacijo, ki jo vsebuje R.

Dodatek

- Vsota: ∀ a ˄ b ∈ R → a + b = c ∈ R

To je algebrski način, da to povem Za vse A in B, ki spada v realna številka, mora biti vsota B, ki je enaka C, ki pripada tudi resničnemu.

Preveriti je enostavno, ali je ta predlog resničen; Dovolj je, da vsoto med katero koli realno število in preverite, ali rezultat pripada tudi resničnim številkam.

3 + 2 = 5 ∈ R

-2 + (-7) = -9 ∈ R

-3 + 1/3 = -8/3 ∈ R

5/2 + (-2/3) = 11/6 ∈ R

Opazimo, da je stanje zaklepanja izpolnjeno za realne številke in vsoto. Na ta način je mogoče sklepati: Vsota resničnih številk je algebrska ključavnica.

Množenje

- Množenje: ∀ a ˄ b ∈ R → a . B = c ∈ R

Za vse A in B, ki spada v resnične, je množenje A za B enako C, ki pripada tudi resničnemu.

Pri preverjanju z istimi elementi prejšnjega primera opazimo naslednje rezultate.

3 x 2 = 6 ∈ R

-2 x (-7) = 14 ∈ R

-3 x 1/3 = -1 ∈ R

5/2 x (-2/3) = -5/3 ∈ R

To je dovolj dokazov, da sklepamo, da: Pomnoževanje realnih števil je algebrska ključavnica.

To opredelitev je mogoče razširiti na vse dejanske številke, čeprav bomo našli določene izjeme.

Vir: Pixabay.com

Posebni primeri v r

Delitev

Kot poseben primer je razdelitev, kjer je cenjena naslednja izjema:

Vam lahko služi: klasična verjetnost: izračun, primeri, rešene vaje

∀ a ˄ b ∈ R → a / b ∉ r ↔ b = 0

Za vse A in B, ki pripadata R Mora biti med B ne pripada reaisu, če in samo, če je B enak nič.

Ta primer se nanaša na omejitev, da se ne bi mogli razdeliti med ničlo. Ker Zero pripada resničnim številom, potem je sklenjeno, da: lDivizija ni ključavnica v resničnem.

Radio

Obstajajo tudi potencialne operacije, natančneje v vložitvi, kjer so predstavljene izjeme za radikalne moči indeksa navora:

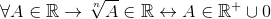; Z n par

Za vse, kar pripada kraljevemu.

Na ta način je označeno.

Logaritem

Je odobren za logaritmično funkcijo, ki ni definirana za vrednosti manjše ali enake nič. Če želite preveriti, ali je logaritem R zaklep, nadaljuje na naslednji način:

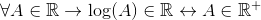
Za vse, za kar spada v reais, logaritem A pripada reaisom, če in samo, če pripada pozitivnemu resničnemu.

Ko so izključene negativne in ničelne vrednosti, ki pripadajo tudi R, je mogoče potrditi, da:

Logaritem ni ključavnica resničnih številk.

Primeri

Preverite ključavnico za vsoto in odštevanje naravnih števil:

Vsota v n

Prva stvar je, da preverite pogoj zaklepanja za različne elemente danega niza, kjer je, če opazimo, da se nekaj elementov lomi s pogojem, lahko obstoj ključavnice samodejno zavrne.

Vam lahko služi: konvergenčni radio: definicija, primeri in vaje rešene

Ta lastnost je izpolnjena za vse možne vrednosti A in B, kot je opaženo v naslednjih operacijah:

1 + 3 = 4 ∈ N

5 + 7 = 12 ∈ N

1000 + 10000 = 11000 ∈ N

Ni naravnih vrednosti, ki bi kršile stanje zaklepanja, zato je sklenjeno:

Vsota je ključavnica v n.

Odšteje v n

Naravni elementi so sposobni razbiti stanje; A - b pripada domorodcem.

Delovanje je enostavno najti pare naravnih elementov, ki ne ustrezajo stanju zaklepanja. Na primer:

7 - 10 = -3 ∉ a n

Tako lahko sklepamo, da:

Odštevanje ni ključavnica nabora naravnih številk.

Predlagane vaje

1-samp.

2-razjasnjen, če je nabor realnih številk zaklepanje celotnih številk.

3-determin, kateri numerični niz je lahko zaklepanje resničnih številk.

4 Vzorčite lastnost zaklepanja za nabor namišljenih števil, glede na vsoto, odštevanje, množenje in delitev.

Reference

1. Panorama čiste matematike: Bourbakist izbira. Jean Dieudonné. Reverte, 1987.
2. Teorija algebrskih številk. Alejandro J. Díaz Barriga, Ana Irene Ramírez, Francisco Tomás. Nacionalna avtonomna univerza v Mehiki, 1975.
3. Linearna algebra in njegove aplikacije. Sandra Ibeth Ochoa García, Eduardo Gutiérrez González.
4. Algebrske strukture V: Teorija telesa. Héctor a. Merklen. Organizacija ameriških držav, General sekretariat, 1979.
5. Uvod v komutativno algebro. Michael Francis Atiyah, jaz. G. MacDonald. Reverte, 1973.