Nelinearne metode programiranja in vaje

The Nelinearno programiranje Gre za postopek optimizacije funkcije, ki je odvisna od več neodvisnih spremenljivk, ki so posledica omejitev.

Če ena ali več omejitev ali če je funkcija čim bolj maksimirana ali zmanjšana (imenovana Ciljna funkcija), se ne izraža kot linearna kombinacija spremenljivk, zato obstaja problem nelinearnega programiranja.

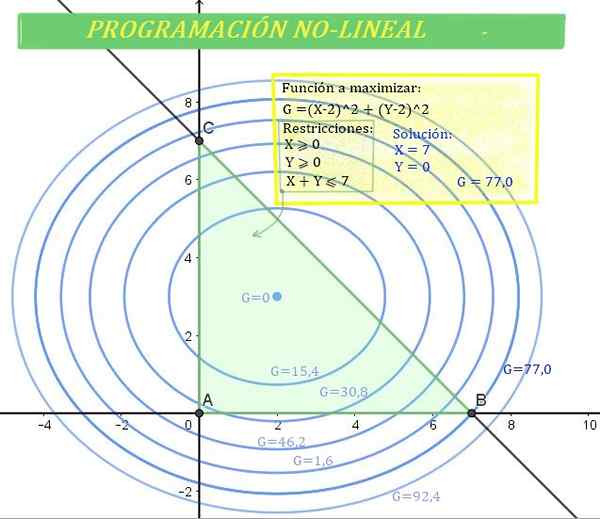
Slika 1. Problem nelinearnega programiranja (NLP). v kateri je g funkcija (nelinearna) za optimizacijo v zeleni regiji, določena z omejitvami. Vir: f. Zapata.

In zato postopkov in metod linearnega programiranja ni mogoče uporabiti.

Na primer, dobro znane metode ni mogoče uporabiti Simplex, ki velja samo, kadar so ciljna funkcija in omejitve vsa linearna kombinacija spremenljivk problema.

[TOC]

Metode linearnega programiranja

Za nelinearno programiranje so glavne metode, ki jih je treba uporabljati: 

1.- Grafične metode.

2.- LAGRANGE MILLPIPIRARJI za raziskovanje meje regije raztopine.

3.- Izračun gradienta za raziskovanje koncev ciljne funkcije.

4.- Metoda spuščanja korakov, da bi našli ničelne točke gradienta.

5.- Spremenjena metoda lagrange multiplikatorjev (s pogojem Karush-kuhn-tuckerja).

Primer rešitve z grafično metodo

Primer rešitve z grafično metodo je tisto, kar je razvidno iz slike 2:

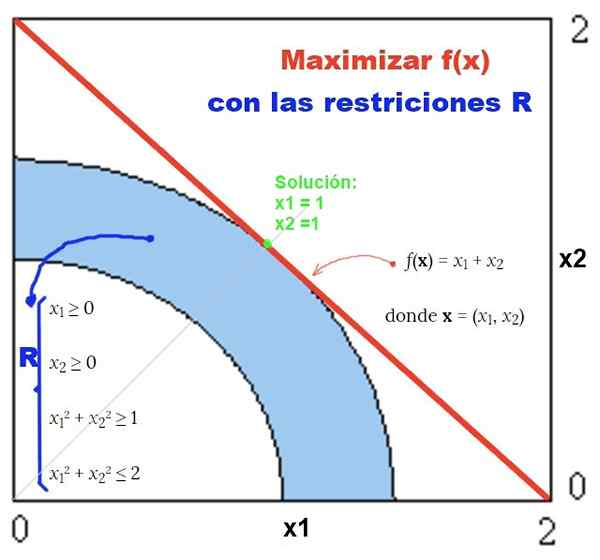Slika 2. Primer nelinearnih problemov z nelinealnimi omejitvami in njeno grafično rešitev. Vir: f. Zapata.

Vaje

- Vaja 1 (grafična metoda)

Dobiček G določenega podjetja je odvisen od zneska, ki je prodana izdelka X, in zneska, prodanega izdelka, poleg tega pa dobiček določi naslednja formula:

Vam lahko služi: konjugirani binomial: kako je rešena, primeri, vaje

G = 2 (x - 2)² + 3 (in - 3)²

Znano je, da imata zneska x in y naslednje omejitve:

X≥0; Y≥0 in x + in ≤ 7

Določite vrednosti x in y, ki proizvajajo največji dobiček.

Slika 3. Dobiček podjetja je mogoče matematično modelirati, da najdemo največji dobiček s pomočjo nelinearnega programiranja. Vir: Pixabay.

Rešitev 

V tem problemu ciljna funkcija ni linearna, medtem ko so neenakosti, ki opredeljujejo omejitve. Je problem Nelinearno programiranje.

Za rešitev tega problema bo izbrana grafična metoda.

Najprej bo določena regija raztopine, ki jo dajejo omejitve.

Kot x≥0; Y≥0, rešitev mora iskati v prvem kvadrantu ravnine XY, vendar pa je treba poleg tega izpolniti, da je x + y ≤ 7, rešitev v spodnjem semiplanu črte x + y = 7.

Raztopino je presečišče prvega kvadranta z spodnjim semiplanom črte, ki povzroča trikotno območje, kjer se nahaja rešitev. Je enako, kot je prikazano na sliki 1.

Po drugi strani je lahko GAIN G predstavljen tudi v kartezijanski ravnini, saj je njegova enačba enačba elipse s centrom (2,3).

Elipsa je prikazana na sliki 1 za več vrednosti G. Višja vrednost g, večji dobiček.

Obstajajo rešitve, ki pripadajo regiji, vendar ne dajejo največje vrednosti G, drugi, na primer G = 92.4 so zunaj zelene cone, torej območje raztopine.

Nato najvišja vrednost G, tako da x e y pripada regiji raztopine, ustreza: 

Vam lahko služi: teoretična verjetnost: kako jo izvleči, primeri, vaje

G = 77 (največji dobiček), ki se pojavi za x = 7 e y = 0. 

Zanimivo je, da se največji dobiček zgodi, ko je količina prodaje izdelka in je nična, medtem ko količina izdelka X doseže največjo možno vrednost.

- Vaja 2 (Analitična metoda: LAGRANGE MILLIPIRARJI) 

Poiščite rešitev (x, y), ki je funkcija f (x, y) = x² + 2 in² biti največji v regiji g (x, y) = x² + in² - 1 = 0.

Rešitev

Jasno je, da nelinearni problem programiranja, saj tako ciljna funkcija f (x, y) kot omejitev g (x, y) = 0 nista linearna kombinacija spremenljivk x in y.

Uporabljena bo metoda LaGrange Multiphipers, ki najprej zahteva določitev funkcije LaGrange l (x, y, λ):

L (x, y, λ) = f (x, y) - λ g (x, y) = x² + 2 in² - λ (x² + in² - 1) 

Kjer je λ parameter, ki se imenuje Lagrange množitelj.

Za določitev ekstremnih vrednosti ciljne funkcije F v regiji raztopine, ki jo daje omejitev g (x, y) = 0, sledijo tem korakom:

-Poiščite delne derivate funkcije Lagrange L glede na x, y, λ.

-Vsaka vsaka derivat.

Tukaj zaporedje teh operacij:

1. ∂l/∂x = 2x - 2λx = 0
2. ∂l/∂y = 4y - 2λy = 0
3. ∂l/∂λ = -(x² + in² - 1) = 0

Možne sistemske rešitve

Možna rešitev tega sistema je λ = 1, da se izpolni prvo enačbo, v tem primeru y = 0.

Ta rešitev pomeni, da je x = 1 ali x = -1, tako da je tretja enačba izpolnjena. Na ta način sta bili pridobljeni dve rešitvi S1 in S2:

S1: (x = 1, y = 0)

S2: (x = -1, y = 0).

Druga možnost je, da je λ = 2 za izpolnjevanje druge enačbe, ne glede na vrednost in.

Lahko vam služi: fermat mejo: kaj je sestavljeno in rešene vaje

V tem primeru je edini način, da je prva enačba izpolnjena, da je x = 0. Glede na tretjo enačbo obstajata le dve možni rešitvi, ki ji bosta rekli S3 in S4:

S3: (x = 0, y = 1)

S4: (x = 0, y = -1)

Če želite vedeti, katera od teh rešitev maksimira ciljno funkcijo, nadaljujte z nadomeščanjem v F (x, y):

S1: F (1, 0) = 1² + 2.0² = 1

S2: F (-1, 0) = (-1)² + 2.0² = 1

S3: F (0, 1) = 0² + 2.1² = 2

S4: F (0, -1) = 0² + enaindvajset)² = 2

Zaključujemo, da sta rešitve, ki maksimirajo F, ko X in Y pripadata obodu g (x, y) = 0, S3 in S4.

Pari vrednosti (x = 0, y = 1) y (x = 0, y = -1) maksimizirajo f (x, y) v regiji raztopine g (x, y) = 0.

- Vaja 3 (NULL Gradient)

Poiščite rešitve (x, y) za ciljno funkcijo:

f (x, y) = x² + 2 in²

Biti največji v regiji g (x, y) = x² + in² - 1 ≤ 0.

Rešitev

Ta vaja je podobna vaji 2, vendar se območje raztopine (ali omejitev) razširi na notranje območje oboda G (x, y) = 0, to je na krog G (x, y) ≤ 0. To vključuje obod in njegovo notranjo regijo.

Mejna rešitev je bila že določena v vaji 2, vendar je treba raziskati notranjo regijo.

Če želite to narediti, je treba izračunati gradient funkcije f (x, y) in enak nič. To je enakovredno izračunu delnih derivatov F glede na X oziroma in izenačenje nič:

∂f/∂x = 2 x = 0

∂f/∂y = 4 y = 0

Ta sistem enačb ima edino rešitev (x = 0, y = 0), ki spada v krog g (x, y) ≤ 0.

Nadomeščanje te vrednosti v rezultatih funkcije f:

f (0, 0) = 0

Za zaključek je največja vrednost, ki prevzame funkcijo v območju raztopine, 2 in se pojavi na meji območja raztopine, za vrednosti (x = 0, y = 1) y (x = 0, y = -1).

 Reference

1. Avriel, m. 2003. Nelinearno programiranje. Založba Dover.
2. Bazaraa. 1979. Nelinearno programiranje. John Wiley & Sons.
3. Bertsekas, d. 1999. Nelinearno programiranje: 2. izdaja. Athena Scientific.
4. Nocedal, J. 1999. Numerična optimizacija. Springer-Verlag.
5. Wikipedija. Nelinearno programiranje. Okrevano od: je.Wikipedija.com