Linearno programiranje, za kaj je, modeli, omejitve, aplikacije

The linearno programiranje Gre za matematično metodo, ki služi za optimizacijo (maksimiranje ali zmanjšanje, kot je potrebno) funkcija, katere spremenljivke so podvržene omejitvam, dokler sta funkcija in omejitve linearno odvisna od spremenljivk.

Na splošno je funkcija za optimizacijo praktičnih razmer, na primer dobiček proizvajalca, katerega vložki, delovna sila ali stroji so omejeni.

Slika 1. Linearno programiranje se pogosto uporablja za optimizacijo dobička. Vir: Piqsels.

Eden najpreprostejših primerov je linearna funkcija za maksimiranje, ki je odvisna le od dveh spremenljivk, imenovanih Spremenljivke odločitve. Lahko je obrazec:

Z = k₁x + k₂in

S k₁ in k₂ konstante. Ta funkcija je znana kot Ciljna funkcija. Seveda obstajajo situacije, ki zaslužijo več kot dve spremenljivki za njihovo študijo, saj so bolj zapletene:

Z = k₁x₁ + k₂x₂ + k₃x₃ +.. .

In omejitve so tudi matematično modelirane s sistemom enačb ali neenakosti, enako linearno v x in in.

Nabor rešitev tega sistema se imenuje izvedljive rešitve tudi izvedljive točke. In med izvedljivimi točkami je vsaj ena, ki optimizira ciljno funkcijo.

Linearno programiranje je neodvisno razvil ameriški fizik in matematik.

Metoda reševanja problemov, znana kot Metoda simpleksa To je ustvarjanje Dantziga, ki je delal za ameriške zračne sile, univerzo v Berkeleyju in univerzi Stanford.

Slika 2. Matematiki George Dantzig (levo) in Leonid Kantorovič (desno). Vir: f. Zapata.

[TOC]

Modeli linearnih programiranja

Potrebni elementi za vzpostavitev linearnega programskega modela, ki je primeren za praktično situacijo, so:

-Ciljna funkcija

-Spremenljivke odločitve

-Omejitve

V ciljni funkciji je definirano tisto, kar želite doseči. Recimo, da je zaželeno povečati dobiček, pridobljen s proizvodnjo nekaterih izdelkov. Potem se vzpostavi funkcija "dobiček", glede na ceno, po kateri se izdelki prodajajo.

V matematičnem smislu lahko to funkcijo izrazimo skrajšano z uporabo seštevanja:

Z = ∑k_Yo x_Yo

V tej enačbi k_Yo So koeficienti in x_Yo so spremenljivke odločitve.

Spremenljivke odločanja so elementi sistema, katerega nadzor je, njihove vrednosti pa so pozitivne realne številke. V predlaganem primeru so spremenljivke odločitve znesek vsakega izdelka, ki ga je treba izdelati za pridobitev največjega dobička.

Končno imamo omejitve, ki so linearne enačbe ali neenakosti glede na spremenljivke odločitve. Opisujejo omejitve težave, ki so znani in so lahko na primer količine surovin, ki so na voljo v proizvodnji.

Vam lahko služi: funkcije višje od dveh (primeri)

Vrste omejitev

Lahko imate znesek m omejitev, začenši od J = 1 do J = m. Matematično so omejitve treh vrst:

1. Do_J = ∑ a_ij . x_Yo
2. B_J ≥ ∑ b_ij . x_Yo
3. C_J ≤ ∑ c_ij . x_Yo

Prva omejitev je linearne vrste enačbe in pomeni, da vrednost_J, kar je znano, je treba spoštovati.

Preostali dve omejitvi sta linearna neenašanja in pomeni, da vrednosti B_J in c_J, znano, ga je mogoče spoštovati ali premagati, kadar je simbol, ki se pojavi, ≥ (večji ali enak) ali spoštovanje ali ne premagati, če je simbol ≤ (manjši ali enak).

Primer modela

Področja uporabe so zelo raznolika, ki zajemajo od poslovne uprave do prehrane, vendar za razumevanje metode je predlagan preprost model praktične situacije z dvema spremenljivkama.

Lokalno pecivo je znano po dveh posebnostih: črna torta iz džungle in torta Sacrista.

V svoji izdelavi potrebujejo jajca in sladkor. Za črno džunglo je potrebnih 9 jajc in 500 g sladkorja, medtem ko je za Sacripenin potrebno 8 jajc in 800 g sladkorja. Ustrezne prodajne cene znašajo 8 in 10 dolarjev.

Težava je: koliko tort vsake vrste bi moralo pecivo povečati svoj dobiček, vedoč, da ima 10 kilogramov sladkorja in 144 jajc?

Spremenljivke odločitve

Spremenljivke odločitve sta "x" in "y", ki sprejmejo resnične vrednosti:

-X: Količina črnih tort iz džungle

-Y: Sacriphantinske torte.

Omejitve

Omejitve so navedene z dejstvom, da je število tort pozitiven znesek in da so za njihovo pripravo omejene količine surovin.

Zato te omejitve na matematični način pridobijo obrazec:

1. x ≥ 0
2. in ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 in ≤ 10

Omejitve 1 in 2 predstavljata Stanje ne -negativnosti prej izpostavljeni in vse zbrane neenakosti so linearne. V omejitvah 3 in 4 sta vrednosti, ki jih ne smemo premagati: 144 jajc in 10 kg sladkorja.

Ciljna funkcija

Končno je ciljna funkcija dobiček, pridobljen z izdelavo "x" količine črnih tort iz džungle in "y" količine zakristije. Zgrajena je pomnoževalna cena glede na količino narejenih tort in dodajanje za vsako vrsto. To je linearna funkcija, ki jo bomo poklicali G (x, y):

G = 8x + 10y

Metode rešitve

Med različnimi metodologijami rešitve so grafične metode, algoritem simpleksa in metoda notranje točke, če omenjam nekaj.

- Grafična ali geometrijska metoda

Ko imate težavo dveh spremenljivk, kot je prejšnji razdelek, omejitve določajo poligonalno območje v ravnini Xy, KLIČITE izvedljiva regija tudi Območje preživetja.

Slika 3. Izvedljivo območje, kjer se nahaja rešitev problema optimizacije. Vir: Wikimedia Commons.

Ta regija je zgrajena skozi Restrikcijske črte, ki so črte, pridobljene iz neenakosti omejitev, ki delujejo le z znakom enakosti.

Vam lahko služi: končni niz: lastnosti, primeri, rešene vaje

V primeru pekarne, ki želi optimizirati dobiček, so omejitvene linije:

1. x = 0
2. y = 0
3. 9x +8y = 144
4. 0.5 x + 0.8y = 10

Vse točke v regiji, zaklenjene s temi črtami, so možne rešitve, zato jih je neskončno. Razen v primeru, v katerem je izvedljiva regija prazna, v tem primeru pa težava primanjkuje rešitve.

Na srečo za problem s pecivo izvedljivo regijo ni prazno, imamo spodaj.

Slika 4. Izvedljivo območje problema s pecivom. Ravna črta 0 prečka izvor. Vir: f. Zapata z geogebro.

Optimalna rešitev, če obstaja, je s pomočjo ciljne funkcije. Na primer, ko gre za iskanje največjega dobička G, imate naslednjo vrstico, ki se imenuje Iso-Benefice naravnost:

G = k₁x + k₂in → y = -K₁x / k₂ + G/ k₂

S to vrstico dobimo vsi pari (x, y), ki zagotavljajo dani dobiček G, zato obstaja družina linij glede na vrednost G, vendar vsi z enakim naklonom -K₁ / k₂, tako da so vzporedni naravnost.

Optimalna rešitev

Zdaj je mogoče dokazati, da je optimalna rešitev linearnega problema vedno ekstremna ali točka izvedljive regije. Tako:

Linijska rešitev je najbolj oddaljena od izvora in ima vsaj eno točko skupnega z izvedljivo regijo.

Če ima črta, ki je najbližje izvoru, celoten segment, ki je skupni z izvedljivo regijo, naj bi bilo neskončne rešitve. Ta primer se zgodi, če je naklon linije ISO-Benefits enaka kot v kateri koli drugi vrstici, ki omejuje regijo.

Za naše pecivo so kandidatne točke A, B in C.

- Simplex metoda Dantziga

Grafična ali geometrijska metoda je uporabna za dve spremenljivki. Vendar je bolj zapleteno, kadar obstajajo tri spremenljivke in jih je nemogoče uporabiti za večje število spremenljivk.

Ko gre za težave z več kot dvema spremenljivkama, Metoda simpleksa, ki je sestavljen iz niza algoritmov za optimizacijo objektivnih funkcij. Za izvajanje izračunov se običajno uporabljajo preproste matrike in aritmetika.

Metoda simpleksa se začne z izbiro izvedljive rešitve in preverjanjem, ali je optimalna. Če je to, smo že rešili težavo, če pa ni, se nadaljuje z rešitvijo bližje optimizaciji. Če rešitev obstaja, algoritem z njo v nekaj poskusih.

Vam lahko služi: kakšen je obseg statistike? (S primeri)

Prijave

Linearno in nelinearno programiranje, ki se uporablja na številnih področjih, da bi sprejemali najboljše odločitve za zmanjšanje stroškov in povečanje dobička, ki niso vedno denarne, saj jih je mogoče na primer meriti, če želite skrajšati potreben čas za izvedbo niz operacij.

Tu je nekaj polj:

-Pri trženju se uporablja za iskanje najboljše kombinacije medijev (družbenih omrežij, televizije, tiska in drugih) za oglaševanje določenega izdelka.

-Za dodelitev dela, ki ustreza osebju podjetja ali tovarne, ali jim načrtuje.

-Pri izbiri najbolj hranljive hrane in z najnižjimi stroški v živinoreji in perutninski industriji.

Rešene vaje

- Vaja 1

Graf linearnega modela programiranja, dvignjenega v prejšnjih razdelkih.

Rešitev

Potrebno je graditi niz vrednosti, ki ga določa sistem omejitev, določenih v težavi:

1. x ≥ 0
2. in ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 in ≤ 10

Regija, ki jo dajeta neenakosti 1 in 2, ustreza prvemu kvadrantu kartezijanske ravnine. Kar zadeva nepravičnosti 3 in 4, se začne z iskanjem omejitev:

9x +8y = 144

0.5 x + 0.8y = 10 → 5x + 8y = 100

Izvedljiva regija je štirikotnik, katere točke so točke A, B, C in D.

Najmanjši dobiček je 0, zato je črta 8x + 10 in 10 spodnja meja, linije ISO -BENEFIT.8.

Ta vrednost se razlikuje od pobočij drugih omejitev in ker je izvedljivo območje omejeno, obstaja edinstvena rešitev.

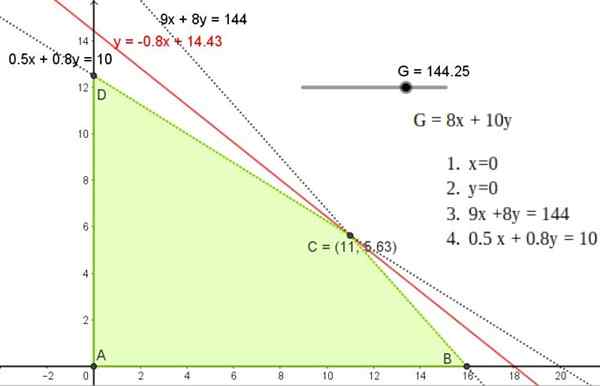Slika 5. Grafična rešitev vaje 1, ki prikazuje izvedljivo regijo in točkovno rešitev C v enem od točk omenjene regije. Vir: f. Zapata.

Ta rešitev ustreza liniji naklona -0.8 To poteka skozi eno od točk A, B ali C, katerih koordinate so:

A (11; 5.625)

B (0; 12.5)

C (16, 0)

Optimalna rešitev

Za vsako od teh točk izračunamo vrednost G:

-(11; 5.625): g_Do = 8 x 11 + 10 x 5.625 = 144.25

-(0; 12.5): g_B = 8 x 0 + 10 x 12.5 = 125

-(16, 0): g_C = 8 x 16 + 10 x 0 = 128

Največji dobiček je izdelava 11 črnih tort iz džungle in 5.625 Sacripantine torte. Ta rešitev se strinja s tisto, ki jo najdemo prek programske opreme.

- Vaja 2

Rezultat prejšnje vaje preverite s funkcijo Solver (Soluterja), ki je na voljo v večini preglednic, kot sta Excel ali Calc De LibreOffice, ki vključuje algoritem simpleksa za linearno programiranje optimizacijo.

Rešitev

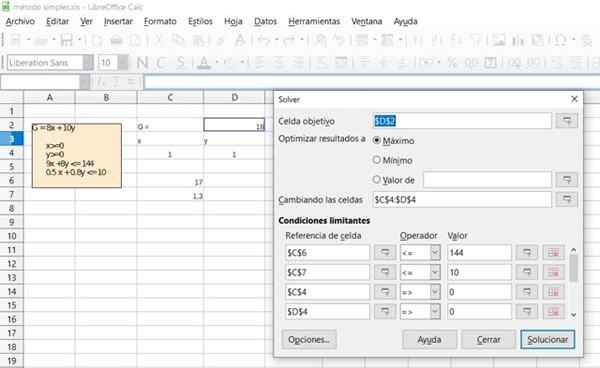Slika 6. Podrobnosti o rešitvi vadbe 1 prek brezplačne preglednice za kalc. Vir: f. Zapata. 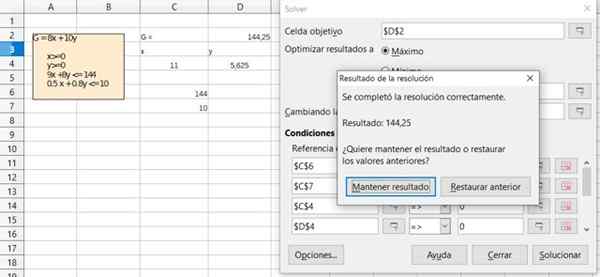Slika 7. Podrobnosti o rešitvi vadbe 1 prek brezplačne preglednice za kalc. Vir: f. Zapata.

Reference

1. Briljantno. Linearno programiranje. Okreval od: briljantno.org.
2. Eppen, g. 2000. Operativne raziskave v administrativni znanosti. 5. Izdaja. Dvorana Prentice.
3. Haeussler, npr. 1992. Matematika za upravo in ekonomijo. 2. mesto. Izdaja. Ibero -ameriška uredniška skupina.
4. Hiru.Eus. Linearno programiranje. Okreval od: Hiru.Eus.
5. Wikipedija. Linearno programiranje. Okrevano od: je. Wikipedija.org.