Teoretična verjetnost, kako to izvleči, primeri, vaje

The Teoretična verjetnost (ali iz Laplacea), da se pojavi dogodek, ki spada v vzorčni prostor S, v katerem imajo vsi dogodki enako verjetnost pojava, je opredeljen v matematični zapisu, kot je: p (e) = n (e) / n ( S)

Kjer je p (e) verjetnost, ki je navedena kot razmerje med skupnim številom možnih rezultatov dogodka E, ki mu pravimo N (e), deljeno s skupnim številom n (s) možnih rezultatov v vzorčnem prostoru S.

Slika 1. Ob izstrelitvi šestih kockov je teoretična verjetnost, da je obraz s tremi pikami na vrhu ⅙. Vir: Pixabay.

Teoretična verjetnost je resnično število med 0 in 1, vendar je pogosto izražena v obliki odstotka, v tem primeru pa bo verjetnost vrednost med 0% in 100%.

Izračun verjetnosti pojava dogodka je zelo pomembno na številnih področjih, kot so dejavnost na borzi, zavarovalnice, igre na srečo in številne druge.

[TOC]

Kako dobiti teoretično verjetnost?

Ilustrativni primer je primer rifa ali loterij. Predpostavimo, da 1.000 vstopnic za pametni telefon Rifar. Ker se žrebanje izvaja naključno, ima katera koli vozovnica enake možnosti, da postane zmagovalec. 

Če želite najti verjetnost, da bo oseba, ki kupi vozovnico s številko 81, zmagovalka, naslednji izračun Teoretična verjetnost:

P (1) = 1/1.000 = 0,001 = 0,1%

Prejšnji rezultat se razlaga na naslednji način: Če se žreba ponavlja neskončno, vsaka 1.000 krat čajna vozovnica 81 bi bila v povprečju izbrana enkrat.

Če iz kakršnega koli razloga nekdo pridobi vse vozovnice, je prepričan, da bo dobil nagrado. Verjetnost osvojitve nagrade, če imate vse vozovnice, izračunane na naslednji način:

Lahko vam služi: obod kroga: kako ga odpeljati ven in formule, rešene vaje

P (1.000) = 1.000/1.000 = 1 = 100%.

To pomeni, kakšna verjetnost 1 ali 100% pomeni, da je popolnoma prepričan, da se bo zgodil ta rezultat.

Če ima nekdo 500 vstopnic, so možnosti zmage ali izgube enake. Teoretična verjetnost osvojitve nagrade v tem primeru se izračuna na naslednji način:

P (500) = 500/1.000 = ½ = 0,5 = 50%.

Kdor ne kupuje nobene vozovnice, nima možnosti za zmago in njegova teoretična verjetnost je določena tako:

 P (0) = 0/1.000 = 0 = 0%

Primeri

Primer 1

Imate valuto z drago na eni strani in ščit ali tesnilo v drugem. Ko se valuta sproži, je teoretična verjetnost dragega?

P (drago) = n (drago) / N ( obraz + ščit ) = ½ = 0,5 = 50%

Rezultat se razlaga na naslednji način: če bi bilo opravljenih ogromno izdaj.

V odstotkih je razlaga rezultata, da bi bilo v povprečju neskončno velikega števila izstrelkov, v povprečju vsakih 100 od njih 50.

Primer 2

V škatli so 3 modri marmorji, 2 rdeča marmor in 1 zelena. Kakšna je teoretična verjetnost, da je, ko dobite marmor iz škatle, to rdeča?

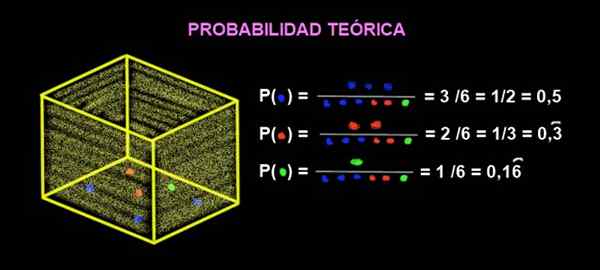Slika 2. Verjetnost ekstrakcije barvnih frnikolov. Vir: f. Zapata.

Verjetnost, ki je rdeča, je:

P (rdeča) = število ugodnih primerov / število možnih primerov

To pomeni:

P (rdeča) = število rdečih marmorjev / skupno število marmorjev

Končno je verjetnost, da je rdeči marmor:

P (rdeča) = 2/6 = ⅓ = 0,3333 = 33,33%

Medtem ko je verjetnost, da je s pridobivanjem zelenega marmorja:

P (zelena) = ⅙ = 0,1666 = 16,66%

Končno je teoretična verjetnost pridobivanja v slepi ekstrakciji modri marmor je: 

P (modra) = 3/6 = ½ = 0,5 = 50%

Lahko vam služi: radikalne lastnosti

Torej od vsakih dveh poskusov bo rezultat v enem od njih in druge barve v drugem poskusu, pod predpostavko, da je izvlečen marmor napolnjen in da je število preskusov zelo, zelo, zelo veliko.

Vaje

Vaja 1

Določite verjetnost, da se pri zagonu kocke vrednost dobi manjša ali enaka 4.

Rešitev

Za izračun verjetnosti, da se ta dogodek zgodi, bo veljala definicija teoretične verjetnosti:

P (≤4) = število ugodnih primerov / število možnih primerov

P (≤5) = 5/6 = = 83,33%

Vaja 2

Poiščite verjetnost, da v dveh zaporednih igriščih običajnih šestih kock, 2 -krat 2 -krat.

Rešitev

Če se želite odzvati na to vajo, je primerno narediti sliko, ki prikazuje vse možnosti. Prva slika označuje rezultat prve kocke, drugo pa rezultat druge.

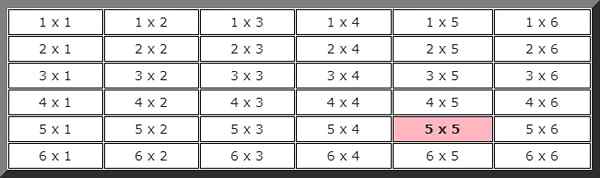
Za izračun teoretične verjetnosti moramo vedeti skupno število možnih primerov, v tem primeru, kot je razvidno iz prejšnje tabele, obstaja 36 možnosti.

Tudi pri opazovanju slike sledi, da je število primerov, ki so naklonjeni dogodku, da je v obeh zaporednih izdajah 5 le 1, poudarjeno z barvo, zato je verjetnost, da se bo ta dogodek zgodil:

P (5 x 5) = 1/33.

Ta rezultat bi lahko dosegli tudi z eno od lastnosti teoretične verjetnosti, ki navaja, da je kombinirana verjetnost dveh neodvisnih dogodkov posledica njihovih posameznih verjetnosti.

V tem primeru je verjetnost, da je v prvi izdaji 5 ⅙. Druga lansiranje je popolnoma neodvisen od prvega, zato je verjetnost, da je tudi 5 v drugem. Torej kombinirana verjetnost je:

Vam lahko služi: delni derivati: lastnosti, izračun, vaje

P (5 × 5) = p (5) p (5) = (1/6) (1/6) = 1/36.

Vaja 3

Poiščite verjetnost, da se v prvem izstrelitvi izide številka manj kot 2, v drugem. 

Rešitev

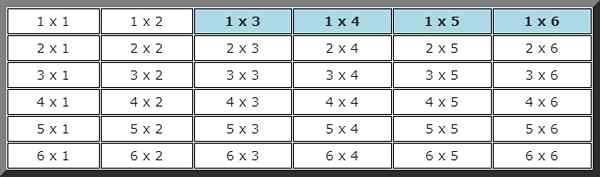
Spet morate zgraditi možno mizo prireditev, kjer tisti, v kateri je bila prva izstrelitev manjša od 2, in v drugem višji od 2 so poudarjeni.

Skupno je 4 možnosti skupno 36. Z drugimi besedami, verjetnost tega dogodka je:

P (2) = 4/36 = 1/9 = 0,1111 = 11,11%

Uporaba teorema o verjetnosti, ki navaja:

Verjetnost pojavljanja dveh neodvisnih dogodkov je enaka produktu posameznih verjetnosti.

Dobimo enak rezultat:

P (2) = (1/6) (4/6) = 4/36 = 0,1111 = 11,11%

Vrednost, pridobljena s tem postopkom, sovpada s prejšnjim rezultatom s teoretično ali klasično definicijo verjetnosti.

Vaja 4

Kakšna je verjetnost, da je z izstrelitvijo dveh glede na vsoto vrednosti 7.

Rešitev

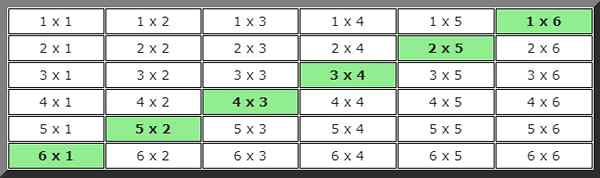
Za iskanje rešitve v tem primeru je bila razvita slika možnosti, v kateri so primeri, ki ustrezajo pogoju vrednosti, 7.

Če pogledamo mizo, je mogoče šteti 6 možnih primerov, zato je verjetnost:

P (R & D II: 7) = 6/36 = 1/6 = 0,1666 = 16,66%

Reference

1. Canavos, g. 1988. Verjetnost in statistika: aplikacije in metode. McGraw Hill.
2. Devore, j. 2012. Verjetnost in statistika za inženirstvo in znanost. 8. Izdaja. Cengage.
3. Lipschutz, s. 1991. Serija Schauma: verjetnost. McGraw Hill.
4. Obregón, i. 1989.Teorija verjetnosti. Uredništvo Limusa.
5. Walpole, r. 2007. Verjetnost in statistika za inženirstvo in znanost. Pearson.