Matematika

Pentagonalne značilnosti prizme, deli, točki, robovi, volumen

Pentagonalne značilnosti prizme, deli, točki, robovi, volumen

A Petegonalna prizma Gre za tridimenzionalno geometrijsko figuro, katere baze, enake, imajo pentagonsko obliko in imajo tudi 5 -strani v obliki paralelograma.

Če so obrazi pravokotni, pravijo, da gre za Ravna petegonalna prizma, Medtem ko so robovi nagnjeni k osnovam, potem je to poševna pentagonalna prizma. Na naslednji sliki je primer vsakega.

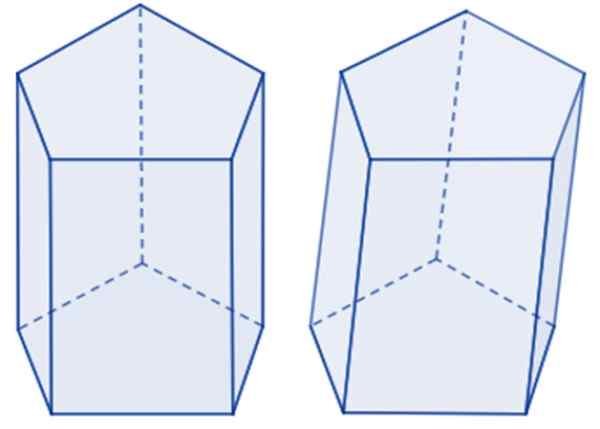Petegonalna prizma levo in poševno na desni. Vir: Wikimedia Commons.

Osnovni pentagon je lahko reden, če ima pet strani enak ukrep, pa tudi notranje kote, sicer gre za nepravilen pentagon. Če je baza prizme redna, gre za približno Navadna petegonalna prizma. Sicer je prizma nepravilno petegonalno.

Nepravilne baze petegonalne prizme, ki se uporabljajo v sodobni konstrukciji. Vir: Ozadje FLARE.

Pentagonalna prizma je harmonična struktura, ki se uporablja pri arhitekturi in oblikovanju predmetov, kot je sodobna zgradba, prikazana na zgornji sliki. Nepravilna okna v obliki Pentagona tvorijo osnovo prizm.

[TOC]

Pentagonalne lastnosti prizme

-Gre za tridimenzionalno geometrijsko figuro, površine, ki jo sestavljajo.

-Njihove baze so pentagoni in njihovi stranski obrazi so lahko pravokotniki ali paralelogrami.

-Ima vrhove -vogale prizme -in robov -bard ali obale-.

-Če so robovi, ki združujejo baze, pravokotni nanje, je prizma naravnost in če so nagnjeni, je prizma poševna.

-Ko je osnova pentagon, katerega notranji koti so manjši od 180 °, je prizma konveksna, Če pa je eden ali več notranjih kotov večji od 180 °, je prizma konkavno.

Pentagonalni prizmatični elementi

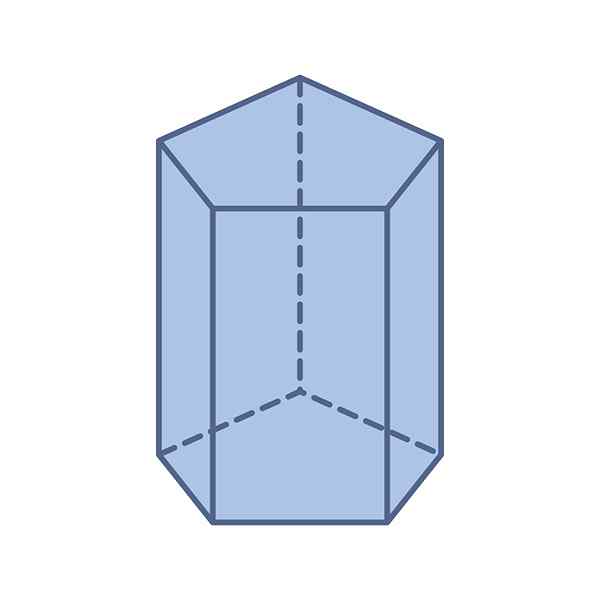
-Baze: Ima dve petegonski in skladni bazi -Njihove meritve so enake -tako redne ali nepravilne.

Vam lahko služi: Splošna formula: kvadratne enačbe, primeri, vaje

-Obraze: Pentagonalna prizma ima skupno 7 obrazov: dve peterokotni bazi in pet paralelogramov, ki sestavljajo stranice.

-Rob: segment, ki se pridruži dve bazi, prikazan v rdeči barvi na sliki 3, ali tistega, ki se pridruži dvema stranicama.

-Višina: Razdalja med obrazi. Če je prizma ravna, ta razdalja sovpada z velikostjo roba.

-Vertex: Skupna točka med osnovno in dvema stranskima stranema.

Spodnja slika prikazuje navadno osnovno pentagonalno prizmo, v kateri imajo segmenti, ki tvorijo osnovo do.

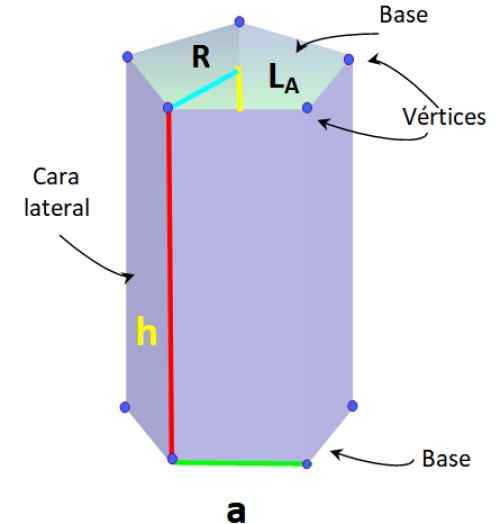 Redni petegonski elementi prizme. Vir: f. Zapata.

Ta vrsta prizme ima tudi naslednje elemente, značilne za običajni pentagon:

-Radio r: Razdalja med središčem pentagona in enim od tokov.

-Apothem lDo: Segment, ki se pridruži sredini s sredino ene od strani Pentagona.

Koliko tokov ima petegonalna prizma?

V Pentagonu je 5 vrhov in ker ima petegonalna prizma dva pentagona kot baze, ima to telo skupno 10 tokov.

Koliko robov ima petegonalna prizma?

Lahko izračunate število robov za geometrijska telesa z ravnimi obrazi, kot so prizme, z uporabo Eulerjev teorem Za konveksne polihedro. Leonhard Euler (1707-1783) je eden največjih matematikov in fizičnih v zgodovini.

Teorem vzpostavlja razmerje med številom obrazov, ki jih bomo poimenovali C, količino vrhov V in skupnimi robovi A na naslednji način:

C+V = A+2

Za petegonsko prizmo imamo: c = 7 in v = 10. Čiščenje, število robov:

Lahko vam služi: bijjektivna funkcija: kaj je to, kako je to, primeri, vaje

A = C+V-2

Zamenjava vrednosti:

A = 7 + 10 - 2 = 15

Petegonalna prizma ima 15 robov.

Kako dobiti količino petegonske prizme?

Prostornina petegonalne prizme meri prostor, ki ga zaklene stranice in baze. To je pozitiven znesek, ki se izračuna z naslednjo lastnostjo:

Vsako ravnino, ki se reže na prizmo, pravokotno na robove, ustvari križišče na enak način kot podlaga, torej pentagon istih dimenzij.

Zato je prostornina petegonske prizme produkt osnovnega območja in višine prizme.

Biti DoB peclagonalno osnovno območje in h Višina prizme, nato glasnost V je:

V = aB x h

Ta formula je splošna, ki velja za katero koli prizmo, redno ali nepravilno, ravno ali poševno.

Obseg prizme vedno prihaja v enotah dolžine visoko do kocke. Če sta dolžina strani in višina prizme podana v metrih, potem je prostornina izražena v m3, da se bere "kubični metri". Druge enote vključujejo CM3, km3, palcev3 in več.

- Redni pentagonalni volumen prizme

V petegonalni prizmi so redne baze redni pentagoni, kar pomeni, da sta stranski in notranji koti enaki. Glede na simetrijo telesa se območje Pentagona in s tem volumen enostavno izračuna na več načinov:

Poznavanje višine in merjenja strani

Biti do Ukrep peteganalne bazne strani. V tem primeru se območje izračuna z:

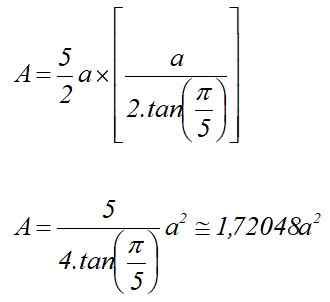
Zato je volumen običajne petegonske prizme višine h:

Vam lahko služi: namišljene številke: lastnosti, aplikacije, primeri

V = 1.72048 a2⋅ h

Poznavanje višine in mere radia

Ko Radio r Iz peteganalne baze se lahko ta druga enačba uporabi za osnovno območje:

A = (5/2) r2⋅ sena 72 °

Na ta način je glasnost peteganske prizme podana z:

V = (5/2) r2 ⋅ H ⋅ sena 72 °

Kje h To je višina prizme

Poznavanje višine, mere vrednosti apotema in oboda

Pentagonalno osnovno območje je mogoče izračunati, če je znan njegov obod P, ki je preprosto vsota strani, pa tudi merilo apotema l l lDo:

A = p. LDo / 2

Pomnožitev tega izraza z vrednostjo višine h, Imamo glasnost prizme:

V = Str. LDo .H / 2

- Nepravilen petegonalni volumen prizme

Formula, podana na začetku, je veljavna celo, kadar je osnova prizme nepravilen pentagon:

V = aB x h

Za izračun osnovnega območja se na primer uporabljajo različne metode:

-Metoda triagulacije, ki je sestavljena iz delitve pentagona na trikotnike in štirikolesnike, katerih območja so zlahka izračunana. Območje Pentagona bo vsota območij teh preprostejših številk.

-Gaussova metoda Determinants, za katero morate poznati točke slike.

Ko je vrednost območja določena, se pomnoži z višino prizme, da dobi prostornino.

Reference

  1. Aleksander, d. 2013. Geometrija. 5. Izdaja. Cengage učenje.
  2. Open Reference Math Open. Območje poligona. Okreval od: Mathpenref.com.
  3. Formule vesolja. Eulerjev teorem za polihedros. Okrevano od: univerzeformulas.com.
  4. Formule vesolja. Območje navadnega pentagona. Okrevano od: univerzeformulas.com.
  5. Wikipedija. Prizma. Okrevano od: je.Wikipedija.com.
  6. Wikipedija. Petegonalna prizma. Okrevano od: je.Wikipedija.com.