Relativni bratranci, kaj so, razlaga, primeri

Je poklican sorodniki (Coprmimos ali bratranci med seboj) na kateri koli par celih števil, ki nimajo skupnega deličarja, razen 1. Z drugimi besedami, dve celotni številki sta relativni bratranci, če v razčlenitvi v primarnih številkah nimata skupnega dejavnika.

Na primer, če sta izbrani 4 in 25. Kot je razvidno, nimajo nobenega skupnega dejavnika, zato sta 4 in 25 relativni bratranci.

Po drugi strani pa, če izberete 6 in 24, pri razčlenitvi v glavnih faktorjih dobimo, da je 6 = 2*3 in 24 = 2³*3.

Kot je razvidno, imata ta zadnja dva izraza vsaj en skupni dejavnik, zato nista relativni bratranci.

Značilnosti relativnih bratrancev

Podrobnost, s katero mora skrb.

Po drugi strani je zgornja definicija mogoče povzeti na naslednji način: Dva cela števila "A" in "B" sta relativna bratranca, če in samo največ skupnega delitve je 1, torej MCD (A, B ) = 1.

Dva takojšnja sklepa te definicije sta:

-Če je "A" (ali "B") prvotna številka, potem MCD (A, B) = 1.

-Če sta "A" in "B" glavni številki, potem MCD (A, B) = 1.

To je, če je vsaj ena od izbranih številk glavna številka, potem so par številk relativni bratranci.

Druge funkcije

Drugi rezultati, ki se uporabljajo za določitev, ali sta dve številki relativni bratranci:

-Če sta dve celotni številki zaporedni, potem sta to relativni bratranci.

-Dve naravni številki "a" in "b" sta relativni bratranci, če, in samo če sta številka "(2^a) -1" in "(2^b) -1" sorodniki.

-Dve celotni številki "a" in "b" sta relativni bratranci, če in le, če pri grafiranju točke (a, b) v kartezijanski ravnini in zgradimo črto, ki poteka skozi izvor (0,0) in (a , b), to ne vsebuje nobene točke s celotnimi koordinatami.

Primeri

1.- Razmislite o celih številkah 5 in 12. Razgradnje v glavnih faktorjih obeh številk sta: 5 oziroma 2²*3. Za zaključek sta MCD (5,12) = 1 torej 5 in 12 sorazmerni bratranci.

2.- Naj številki -4 in 6. Potem -4 = -2² in 6 = 2*3, tako da je MCD (-4,6) = 2 ≠ 1. Za zaključek -4 in 6 nista relativni bratranci.

Če črta, ki poteka skozi urejene pare (-4,6) in (0,0) in za določitev enačbe omenjene črte, je mogoče preveriti, ali to prehaja skozi točko (-2,3).

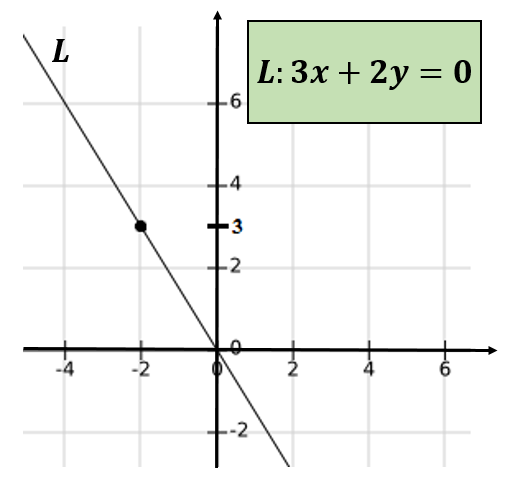
Spet je sklenjeno, da -4 in 6 nista sorodnika.

3.- Številka 7 in 44 sta relativna bratranca in jih je mogoče hitro sklepati po zaslugi zgoraj navedenega, ker je 7 glavna številka.

4.- Razmislite o številkah 345 in 346. Ker je dve zaporedni številki, je preverjeno, da sta MCD (345,346) = 1 torej 345 in 346 relativni bratranci.

5.- Če se upoštevajo številki 147 in 74.

6.- Številki 4 in 9 sta sorodnika. Če ga želite dokazati, lahko uporabite drugo zgoraj omenjeno karakterizacijo. Dejansko je 2^4 -1 = 16-1 = 15 in 2^9-1 = 512-1 = 511.

Pridobljene številke so 15 in 511. Razgradnje v glavnih faktorjih teh številk so 3*5 in 7*73, tako da je MCD (15,511) = 1.

Kot lahko vidite, je uporaba druge karakterizacije daljše in bolj naporno delo za njegovo preverjanje.

7.- Razmislite o številkah -22 in -27. Potem lahko te številke prepišemo na naslednji način: -22 = -2*11 in -27 = -3³. Zato sta MCD (-22, -27) = 1, torej -22 in -27 so relativni bratranci.