Manometrična razlaga tlaka, formule, enačbe, primeri

The Tlak merilnika Str_m To je tisto, ki se meri glede na referenčni tlak, ki je v večini primerov izbran kot atmosferski tlak P_Bankomat na morskem nivoju. Potem je a Relativni tlak, še en izraz, za katerega je znan tudi.

Drugi način, kako se običajno meri tlak, ga primerja z absolutno praznino, katere tlak je vedno nič. V tem primeru govori o absolutni pritisk, Na kar bomo označili, kako p_do.

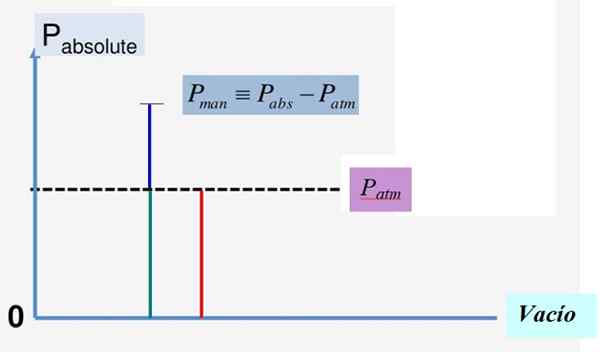
Slika 1. Absolutni tlak in manometrični tlak. Vir: f. Zapata.

Matematični odnos med temi tremi količinami je:

Str_do = P_Bankomat + Str_m

Zato:

Str_m = P_do - Str_Bankomat

Slika 1 priročno ponazarja to razmerje. Ker je vakuumski tlak 0, je absolutni tlak vedno pozitiven in enako velja za atmosferski tlak P_Bankomat.

Manometrični tlak se običajno uporablja za označevanje tlakov nad atmosferskim tlakom, kot je tisti, ki ga nosijo pnevmatike ali tisti na dnu morja ali bazena, ki ga izvaja teža vodnega stolpca. V teh primerih str_m > 0, saj str_do > P_Bankomat.

Vendar pa so pod P absolutni pritiski_Bankomat. V teh primerih str_m < 0 y recibe el nombre de Vakuumski tlak In ga ne bi smeli zamenjati s že opisanim tlakom vakuuma, ki je odsotnost delcev, ki bi lahko izvajali tlak.

[TOC]

Formule in enačbe

Tlak v tekočini -tekočini ali plinu je ena najpomembnejših spremenljivk v svoji študiji. V stacionarni tekočini je tlak enak, kar kaže na isto globino ne glede na orientacijo, medtem ko gibanje tekočin v ceveh povzroča spremembe tlaka.

Povprečni tlak je opredeljen kot količnik med silo, pravokotno na površino F_⊥ in območje omenjene površine A, ki je matematično izraženo na naslednji način:

P = f_⊥ /Do

Tlak je skalarna količina, katere dimenzije so sile na enoto območja. Enote vašega ukrepa v sistemu mednarodnih enot (SI) so Newton/M², v čast Blaise Pascal (1623-1662) se imenuje Pascal in skrajša kot PA.

Večkratniki všeč kilogram (10³) in mega (10⁶) Pogosto se uporabljajo, saj je atmosferski tlak običajno v območju 90.000 - 102.000 Pa, ki je enak: 90 - 102 kPa. Pritiski vrstnega reda mega Pascals niso redki, zato se je treba seznaniti s predponami.

V anglo -saksonskih enotah se tlak meri v kilogramih/stopalu², Vendar je treba storiti v kilogramih/palcu² tudi psi (Kilograma na kvadratni palec).

Vam lahko služi: prenos toplote: zakoni, obrazci za prenos, primeri

Sprememba tlaka z globino

Bolj ko se potopimo v vodo bazena ali v morju, več pritiska doživljamo. Nasprotno, naraščajoča višina se atmosferski tlak zmanjšuje.

Povprečni atmosferski tlak na morskem nivoju je vzpostavljen v 101300 PA ali 101.3 kPa, medtem ko je v jami Mariana v zahodnem Tihem oceanu - največja globina, ki je znana - približno 1000 -krat višja in na vrhu Everesta je le 34 kPa.

Jasno je, da sta tlak in globina (ali višina) povezana. Če želite vedeti v primeru tekočine za počitek (statično ravnovesje), se šteje za del tekočine s tekočino v obliki diska, omejen v posodi (glej sliko 2). Disk ima presek Do, utež Dw in višina Dy.

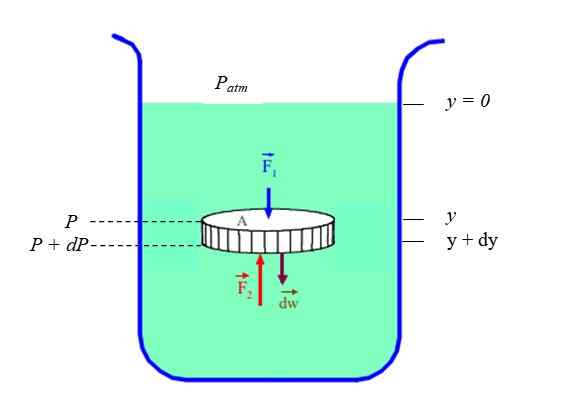Slika 2. Diferencialni element statične ravnotežne tekočine. Vir: Fanny Zapata.

Poklicali bomo Str ob tlaku, ki obstaja v globini "in"in P + DP pri tlaku, ki obstaja v globini (in + dy). Ker je gostota ρ tekočine razlog med njegovo maso Dm in njeno glasnost DV, Moraš:

ρ = dm/ dv ⇒ dm = ρ.DV

Zato teža Dw elementa je:

dw = g. Dm = ρ.g.DV

In zdaj velja drugi zakon Newtona:

Σ f_in = F₂ - F₁ - Dw = 0

(P + DP).A - p.Do - ρ.g.DV = 0

(P + DP).A - p.Do - ρ.g. Do. Dy = 0

Dp = ρ.g.Dy

Raztopina diferencialne enačbe 

Vključevanje obeh strani in upoštevanje te gostote ρ, kot tudi gravitacija g Sta konstantna, obstaja iskan izraz:

Str₂ - Str₁ = ΔP = ρ.g.(in₂ - in₁)

ΔP = ρ.g. Δin

Če je v prejšnjem izrazu izbran Str₁ kot so atmosferski tlak in in₁ Kot površina tekočine in₂ Nahaja se na globini h in ΔP = str₂ - Str_Bankomat To je manometrični tlak, odvisno od globine:

Str_m = ρ.g.h

Če potrebujete absolutno vrednost tlaka, je atmosferski tlak preprosto dodan v prejšnji rezultat.

Primeri

Za manometrični tlak se uporablja naprava merilnik tlaka, ki na splošno ponuja razlike v tlaku. Na koncu bo opisano načelo obratovanja u -sharenega tlaka Manometra, zdaj pa si oglejmo nekaj pomembnih primerov in posledic prej odštete enačbe.

Načelo Pascal

Enačba ΔP = ρ.g.(in₂ - in₁) Lahko ga zapišemo kot  P = po + ρ.g.h, kje Str je tlak na globini h, medtem Str_tudi To je pritisk na površino tekočine Str_Bankomat.

Očitno vsakič, ko se povečate Po, poveča Str v isti količini, dokler gre za tekočino, katere gostota je konstantna. To je točno tisto, kar naj bi upoštevali ρ konstantno in ga postavite zunaj integrala, ki je bil razrešen v prejšnjem razdelku.

Vam lahko služi: preprosto harmonično gibanje

Načelo Pascal pravi, da se vsako povečanje tlaka tekočine, omejene v ravnovesju, prenaša brez kakršnih koli sprememb na vse točke omenjene tekočine. Skozi to lastnost je mogoče pomnožiti silo F₁ nanesemo na majhno levo levo in dobimo F₂ na desni.

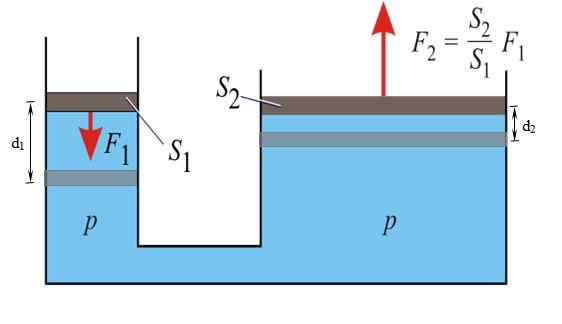Slika 3. V hidravličnem tisku se uporablja načelo Pascal. Vir: Wikimedia Commons.

Avtomobilske zavore delujejo po tem načelu: na stopalko se uporabi razmeroma majhna sila, ki postane glavna sila na zavornem valju na vsakem kolesu, zahvaljujoč tekočini, ki se uporablja v sistemu.

Stevinov hidrostatični paradoks

Hidrostatični paradoks navaja, da je sila zaradi tlaka tekočine na dnu posode lahko enaka, večja ali manjša od teže same tekočine. Toda pri postavljanju posode na lestvico bo običajno zabeležila težo tekočine (seveda ena od posode). Kako razložiti ta paradoks?

Začnemo iz dejstva, da je tlak na dnu vsebnika odvisen izključno od globine in je neodvisen od oblike, kot je bilo sklenjeno v prejšnjem razdelku.

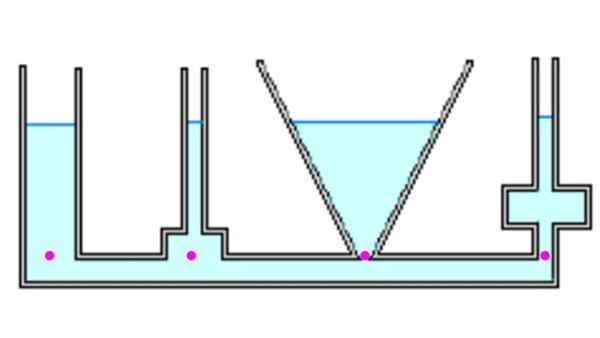Slika 4. Tekočina doseže enako višino v vseh posodah in tlak v ozadju je enak. Vir: f. Zapata.

Poglejmo nekaj različnih zabojnikov. Ko jih komunicirajo, ko so napolnjeni s tekočino, vsi dosežejo enako višino h. Vidne točke so ob enakem pritisku, saj so na isti globini. Vendar se sila zaradi tlaka v vsaki točki lahko razlikuje od teže (glej primer 1 spodaj).

Vaje

Vaja 1

Primerjajte silo, ki jo ima pritisk na dnu vsakega od zabojnikov s težo tekočine, in pojasnite, zakaj razlike, če obstajajo.

Zabojnik 1 

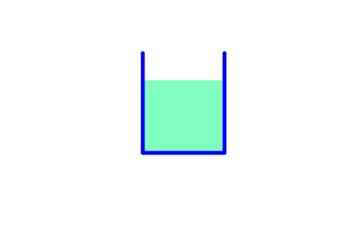Slika 5. Tlak v ozadju je enak velikosti tekočine. Vir: Fanny Zapata.

V tej vsebniki je torej osnovno območje a:

Teža tekočine: mg = ρ.V.G = ρ . Do .h . g

Pritisk na dnu: ρ. g. h

Sila zaradi tlaka: f = p.A = ρ. g. h. Do

Teža in sila zaradi tlaka sta enaka.

Zabojnik 2 

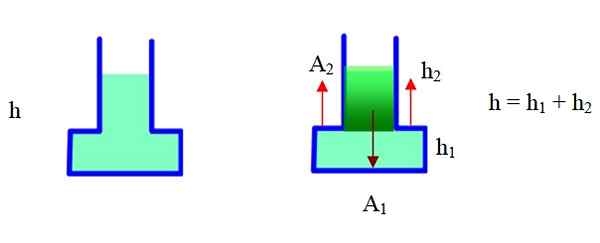Slika 6. Sila zaradi tlaka v tej posodi je večja od teže. Vir: f. Zapata.

Zabojnik ima ozek del in širok del. V desni shemi je bila razdeljena na dva dela in bo geometrija uporabila za iskanje skupne volumna. Območje a₂ je zunaj vsebnika, h₂ Je višina ozkega dela, h₁ To je višina širokega dela (podlaga).

Vam lahko služi: pleide: zgodovina, izvor in sestava

Popolna glasnost je prostornina podstavka + prostornina ozkega dela. S temi podatki imate:

Teža tekočine: m . G = ρ . g. V = ρ . g. [Do₁ .h₁+ (Do₁ -Do₂) .h₂] =

= ρ . g (a₁.ha₂h₂) = ρ . g . Do₁.H - ρ . g . Do._. h₂ (Uporaba h = h₁ +h₂)

Pritisk na dnu: p = ρ. g. h

Sila na dnu zaradi tlaka: f = p. Do₁ = ρ. g. h. Do₁

Če primerjamo težo tekočine s silo zaradi tlaka, je ugotovljeno, da je to večje od teže.

Kar se zgodi, je, da tekočina izvaja tudi trdnost na delu koraka v posodi (glej rdeče puščice slike), ki so vključene v prejšnji izračun. Ta nasprotna sila tistim, ki se izvajajo, in teža, ki jo beleži lestvica, je rezultat teh. V skladu s tem je obseg teže:

W = sila na ozadju - moč na stoječem delu = ρ . g . Do₁.H - ρ . g . Do._. h₂

Vaja 2

Slika prikazuje odprti merilnik tlaka v cevi. Sestavljen je iz U cevi U, v kateri je eden od koncev pri atmosferskem tlaku, drugi pa se poveže s S, sistemom, katerega tlak bo izmerjen.

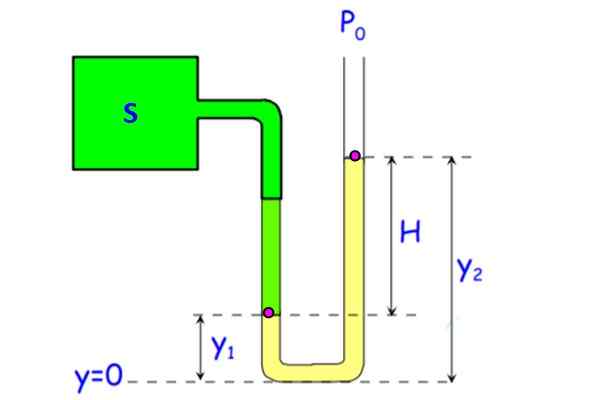Slika 7. Odprti merilnik tlaka v cevi. Vir: f. Zapata.

Tekočina v cevi (na sliki rumene) je lahko voda, čeprav se živo srebro uporablja za zmanjšanje velikosti naprave. (Razlika v 1 atmosferi ali 101.3 KPA zahteva 10 vodni stolpec.3 metre, nič prenosnega).

Zahteva se, da najdete manometrični tlak Str_m V sistemu S, odvisno od višine h tekočega stolpca.

Rešitev

Tlak v ozadju za obe veji cevi je enak, ker je v isti globini. Naj p_Do Pritisk v točki A, ki se nahaja v in₁ In p_B tiste točke B, ki je na vrhuncu in₂. Ker je točka B nameščena v vmesniku za tekočino in zrak, je tlak p_tudi. V tej veji merilnika tlaka je tlak na dnu:

PO + ρ.g.in₂

Po njegovem delu je tlak na dnu za vejo leve:

P + ρ.g.in₁

Kjer je p absolutni tlak sistema in ρ je gostota tekočine. Enaka oba tlaka:

PO + ρ.g.in₂ = P +ρ.g.in₁

Čiščenje Str:

P = po + ρ.g.in₂ - ρ.g.in₁ = PO + ρ.g (in₂ - in₁) = PO + ρ.g. H

Zato manometrični tlak Str_m Daje ga P - P_tudi = ρ.g. H In da ima svojo vrednost, je dovolj, da merite višino, do katere se dvigne manometrična tekočina, in jo pomnoži z vrednostjo g in gostota tekočine.

Reference

1. Cimbala, c. 2006. Mehanika tekočin, osnov in aplikacij. MC. Graw Hill. 66-74.
2. Figueroa, d. 2005. Serija: Fizika za znanost in inženiring. Zvezek 4. Tekočine in termodinamika. Uredil Douglas Figueroa (USB). 3-25.
3. Mott, r. 2006. Mehanika tekočine. 4. Izdaja. Pearson Education. 53-70.
4. Shaugnessy, npr. 2005. Uvod v mehaniko tekočine.Oxford University Press. 51 - 60.
5. Stylianos, v. 2016. Do preproste razlage klasičnega hidrostatičnega paradoksa. Okreval od: haimgaifman.Datoteke.WordPress.com