Elementi Pentadecágono, klasifikacija, značilnosti, vadba

A Pentadecantagon To je ravna figura, zgrajena s petnajstimi ravnimi segmenti in zaprto. Tovrstne številke se imenujejo poligon In imenovani so glede na količino strani, ki imajo.

Trikotnik s tremi stranicami in štirikoletnimi, štirimi, je primeri zelo znanih poligonov, vendar imajo lahko več strani več strani.

Slika 1.  Navadni pentagon z rdečimi tolici. Vir: Wikimedia Commons.

Osnovni elementi Pentadecágona so enaki vsakemu poligonu, ne glede na količino strani, ki jih ima. Ti elementi so:

-Strani, ki so segmenti, ki sestavljajo Pentadecágono za skupno 15.

-Točke, tudi 15, ki so konci sosednjih strani.

-Notranji koti, Tisti, ki se oblikujejo znotraj Pentadecágono med dvema sosednjima stranema.

-Zunanji koti, tvori med eno stranjo in podaljšanje ene od zaporednih strani.

-Diagonale, Linijski segmenti, ki se pridružijo dvema neprimernim tohom.

[TOC]

Klasifikacija

Pentadecágono je lahko redno tudi nepravilno, odvisno od velikosti njihovih strani in mera notranje kote. Če imate vse strani in enake notranje kote - Quilátero in Equiangle - je redno, kot je prikazano na sliki 1, sicer je nepravilno.

Lahko ga tudi razvrstimo po konveksna tudi konkavno. Konkavni pentagon ima enega ali več notranjih kotov, večjih od 180 °, medtem ko ima eden vedno konveksnih notranjih kotov manj kot 180 °. Navadni pentagon je izbočen.

Upošteva se druga merila za razvrščanje, če so njegove nekomerne strani - ali njihove podaljške - razrezane ali ne. Ko jih ne režejo, kot na sliki 1, se reče, da gre za preprost pentadecágon. In če so rezani, potem je zapleteno.

Lahko vam služi: analitična geometrija

Navadni pentagon

Navadni Pentagon, katerega strani in notranji koti imajo enak ukrep, je figura velike simetrije, saj so za predhodno opisane naslednje dodatne elemente:

-Center: Točka, ki je enakovredna točkam in straneh.

-Radio: Razdalja od središča do enega od običajnih vrhov Pentagon.

-Osrednji kot: Tisti, ki ima svojo vrhovo na sredini figure in njenih strani prehaja skozi dve sosednji točki.

-Apotem, Pravokotni segment se pridruži središču ene strani s sredino slike.

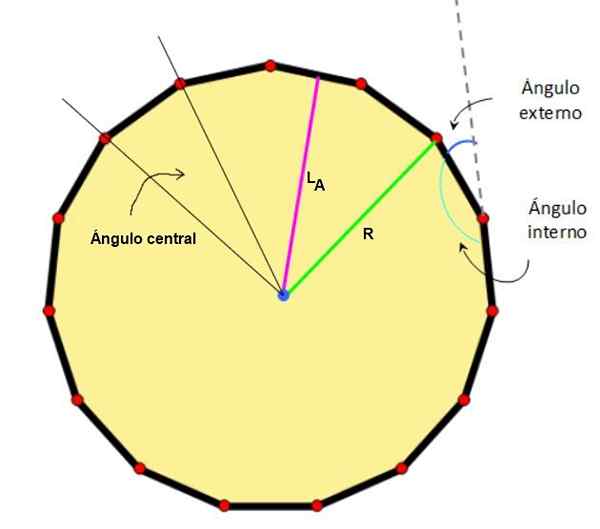Slika 2. Center, apotem, radio in opazni koti Pentadecágona. Vir: Wikimedia Commons/F. Zapata.

- Značilnosti običajnega pentagona

Notranji koti

Naslednja formula se uporablja za izračun ukrepa I notranjih kotov katerega koli rednega poligona, kjer n To je število strani:

V tej formuli je ukrep I nastopi v stopinjah, da ga izrazim v radianih, pomnoži faktor π/180. Poglejmo, kakšna je merilo notranjega kota običajnega pentagona, ki nadomesti n = 15:

I = [(15-2) × 180 °]/15 = 156 °

Enakovredno radianom 13π/15. Ker so notranji koti navadnega pentagona manjši od 180 °, je konveksni poligon.

Vsota notranjih kotov

Vsoto notranjih kotov je mogoče izračunati z naslednjo formulo:

S = (n-2) x 180 °

Kot vedno, n predstavlja število strani. Ta formula velja za n = 3, 4, 5 .. .

Delamo n = 15, dobimo:

S = (15 - 2) x 180 ° = 2340 °

Zunanji koti

Notranji kot in zunanji kot sta dopolnita, torej vsota je 180 °, kot je prikazano na sliki 2. Zato zunanji kot Pentadecágono ukrepov:

Vam lahko služi: konjugirani binomial: kako je rešena, primeri, vaje

180 ° - 156 ° = 24 °.

Obod in območje

Obod je merilo konture poligona in zlahka dodaja vse strani. Ja do Je dolžina strani, dovolj je, da se pomnoži n, Število strani.

Za navaden pentagon strani A je obod P:

P = 15a

Če gre za nepravilno figuro, v kateri se merilo strani razlikuje, obod dodaja dolžino vseh strani.

Kar zadeva območje, ga lahko izračunamo na več načinov. Na primer imamo formulo, ki vam omogoča, da jo pridobite in poznate dolžino A njegovih strani:

Z navedenimi operacijami ostaja približno:

A = 17.6426⋅A²

Obstaja še ena možnost, ki se uporablja za običajne poligone. Gre za to, da jih delimo na osnovne trikotnike, ki so enaki poligonu. Višina trikotnika je dolžina apotema l_Do, definirano zgoraj.

Območje omenjenega trikotnika se izračuna z dobro znano formulo: osnovna x višina /2. Na ta način je območje posameznega trikotnika:

Območje = a. L_Do /2

Če želite imeti skupno površino poligona, je dovolj, da se pomnoži po številu strani N, kar je v tem primeru 15:

A = 15⋅a⋅ l_Do /2

In ker je obod slike p = 15⋅A, potem:

A = p⋅ l_Do /2

Diagonale

Diagonale so segmenti, ki združujejo dve nekomerni točki, kot je navedeno zgoraj. Vedeti, koliko diagonalov ima redni poligon n strani, vključno s Pentadecágono, obstaja naslednja formula:

Kjer je D število diagonalov.

Zdaj nadomestimo n = 15, da dobimo skupne diagonale:

Vam lahko služi: redni poligoni: lastnosti, elementi, koti, primeri

D = [15 × (15-3)]/2 = 90 diagonalov.

Gradnja s pravilom in kompasom

Pentadecágono je zgrajen s pravilom in kompasom, ki se začne iz oboda. 360 ° je treba razdeliti na 15 enakih delov 24 °. Najprej so pomožne konstrukcije, navedene v animaciji.

Slika 3. Gradnja s pravilom in kompasom rednega pentagona. Vir: Wikimedia Commons.

Vaja rešena

Če je obod Pentadecágono, registriranega v krogu polmera R, 12,56 cm. Izračunati:

a) radio.

b) vaše območje.

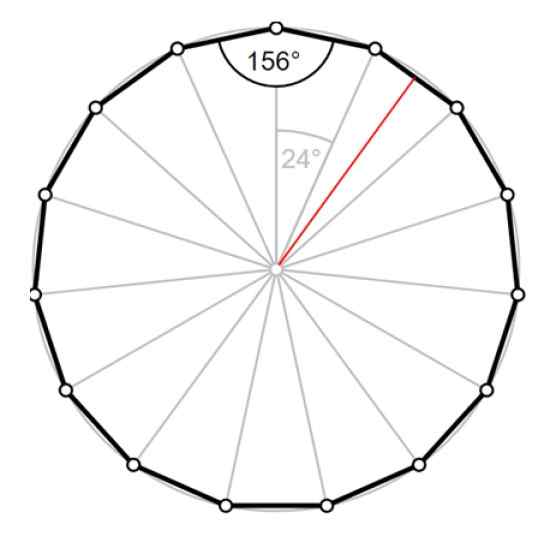Slika 4. Pentadecágono: osrednji kot, notranji kot in rdeča apotema. Vir: Wikimedia Commons/F. Zapata.

Rešitev

Obod je p = 15⋅a = 12.56 cm torej stran Pentadecágono je 0.8373 cm. Radio Lahko ga izračunamo s pomočjo enega od trikotnikov na sliki 4.

Apothem l_Do ustreza višini trikotnika, narisano v rdeči barvi, ki deli kot 24 ° na dva kota 12 °.

Obstajata dva desna trikotnika z notranjim kotom 12 °, za katero koli od njih pa lahko uporabimo trigonometrijo, da najdemo hipotenuzo, ki je dolžina R polmera.

Na ta način:

sen 12 ° = (a /2) /r

R = (a /2) /sen 12º = (0.8373 cm / 2) / sen12º = 2.01 cm.

Rešitev b

Področje Pentadecágono lahko izračunamo s formulo:

A = p⋅ l_Do /2

Že poznamo obod p = 12.56 cm, dolžina apotema pa izračuna tangent ali 12 ° kosinus:

Cos 12 ° = l_Do / R

L_Do = R. cos 12 ° = 2.01 cm. cos 12 ° = 1.97 cm

Zamenjava:

A = 12.56 cm⋅ 1.97 cm /2 = 12.35 cm²

Reference

1. Aleksander, d. 2013. Geometrija. 5. Izdaja. Cengage učenje.
2. Naučite se matematike. Geometrijske figure. Okrevano od: Rodrigoanchorena.WixSite.com.
3. Sangaku matematika. Elementi poligona in njegove klasifikacije. Okreval od: sangakoo.com.
4. Wikipedija. Pentadecágono. Okrevano od: je.Wikipedija.org.
5. Wolfram Math World. Pentadecagon. Okreval od: Mathworld.Wolfram.com.