Papomudas

Kaj je papomudas?

On Papomudas To je postopek za reševanje algebrskih izrazov. Njegov kratica kaže na vrstni red prednostne naloge: oklepaje, pooblastila, množenje, delitev, dodajanje in odštevanje. S to besedo si lahko preprosto zapomnite vrstni red, v katerem je treba rešiti izraz, sestavljen iz več operacij.

Na splošno lahko v numeričnih izrazih najdete več aritmetičnih operacij skupaj, kot so vsote, odštevanje, množenje in delitve, ki so lahko tudi frakcije, moči in korenine. Za njihovo reševanje je treba slediti postopku, ki zagotavlja, da bodo rezultati pravilni.

Aritmetični izraz, ki ga sestavlja kombinacija teh operacij. Tako lahko vsi ljudje sledijo istemu postopku in dobijo enak rezultat.

Značilnosti

Papomudas je standardni postopek, ki določa vrstni red, ki ga je treba upoštevati, ko je treba dati izraz, ki je sestavljen iz kombinacije operacij, kot so vsota odštevanja, množenje in delitev.

Ta postopek določa vrstni red prednostne operacije v zvezi z drugimi v času, ko bodo; to pomeni, da ima vsaka operacija hierarhični premik ali raven, ki jo je treba rešiti.

Vrstni red, v katerem je treba razrešiti različne operacije izraza, daje vsaka kratica besede papomudas. Na ta način morate:

1. PA: oklepaji, kvadratni nosilci ali tipke.
2. PO: Powers and Roots.
3. MU: Multiplication.
4. D: Oddelki.
5. O: Dodatki ali vsote.
6. S: odštevanje ali odštevanje.

Ta postopek se imenuje tudi v angleščini kot pemdas; Za enostavno zapomnitev je ta beseda povezana z besedno zvezo: "Prosim oprostite, draga moja teta Sally", Kjer vsaka začetna črka ustreza aritmetični operaciji, na enak način kot papomudi.

Kako jih rešiti?

Na podlagi hierarhije, ki jo je ustanovil Papomudas za reševanje operacij izraza, je treba izpolniti naslednji vrstni red:

• Najprej je treba rešiti vse operacije, ki so znotraj združevanja simbolov, kot so oklepaji, ključi, oklepaji in palice. Ko obstajajo združevanje simbolov znotraj drugih, začnete izračunati od znotraj.

Vam lahko služi: kvadratni nasledniki: primeri, pravilo in vaje rešene

Ti simboli se uporabljajo za spreminjanje vrstnega reda, v katerem se rešijo operacije, ker je treba vedno rešiti tisto, kar je vedno znotraj teh.

• Potem so moči in korenine rešene.
• Na tretjem mestu se rešujejo množenje in delitve. Ti imajo enak vrstni red; Torej, ko se ti dve operaciji najdemo v izrazu, je treba rešiti tisto, ki se najprej pojavi, brati izraz od leve proti desni.
• Navsezadnje se rešijo vsote in odštevanje, ki imata tudi enak vrstni red, zato je razrešena, ki se najprej pojavi v izrazu, beremo od leve proti desni.
• Operacije nikoli ne smete mešati, če se preberete od leve proti desni, vedno morate upoštevati vrstni red prednostnih nalog ali hierarhijo, ki jo vzpostavi papomudi.

Pomembno si je zapomniti, da mora biti rezultat vsake operacije v enakem vrstnem redu v primerjavi z drugimi, vse vmesne korake.

Aplikacija

Postopek Papomudas se uporablja, kadar imate kombinacijo različnih operacij. Če upoštevamo, kako so rešeni, je to mogoče uporabiti v:

Izrazi, ki vsebujejo vsote in odštevanja

Je ena najpreprostejših operacij, saj imata oba enak vrstni red, tako da ga je treba v izrazu razrešiti, začenši z leve na desno; Na primer:

22 -15 + 8 +6 = 21.

Izrazi, ki vsebujejo vsote, odštevanje in množenje

V tem primeru je največja prednostna operacija množenje, nato pa se rešijo vsote in odštevanje (tista, ki je najprej v izrazu). Na primer:

6 _* 4 - 10 + 8 _* 6 - 16 + 10 _* 6

= 24 -10 + 48 - 16 + 60

= 106.

Izrazi, ki vsebujejo vsoto, množenje odštevanja in delitev

V tem primeru obstaja kombinacija vseh operacij. Začne se z reševanjem množenja in delitve, ki imata vrhunsko prednostno nalogo, nato vsote in odštevanje. Branje izraza od leve proti desni se razreši v skladu z njegovo hierarhijo in položaj znotraj izraza; Na primer:

Vam lahko služi: mamica

7 + 10 _* 13 - 8 + 40 ÷ 2

= 7 + 130 - 8 + 20

= 149.

Izrazi, ki vsebujejo vsoto, odštevanje, množenje, delitev in pooblastila

V tem primeru je ena od številk povišana na moč, ki jo je treba najprej rešiti v prednostni ravni, nato pa rešiti množenje in delitve ter na koncu vsote in odštevanje:

4 + 4² _* 12 - 5 + 90 ÷ 3

= 4 + 16 _* 12 - 5 + 90 ÷ 3

= 4 + 192 - 5 + 30

= 221.

Tako kot pristojnosti imajo tudi korenine drugi vrstni red; Zato jih je treba v izrazih, ki jih vsebujejo, najprej rešiti kot množenje, delitve, vsote in odštevanje:

5 _* 8 + 20 ÷ √16

= 5 _* 8 + 20 ÷ 4

= 40 + 5

= 45.

Izrazi, ki uporabljajo simbole za razvrščanje

Ko se uporabljajo znaki, kot so oklepaji, ključi, oklepaji in palice, ki so znotraj teh, se najprej rešijo, ne glede na vrstni red prednostne naloge, ki jih vsebuje v zvezi s tistimi, ki niso zunaj tega Izraz:

14 ÷ 2 - (8 - 5)

= 14 ÷ 2 - 3

= 7 - 3

= 4.

Če je znotraj tega več operacij, jih je treba rešiti s hierarhičnim redom. Potem so rešene druge operacije, ki sestavljajo izraz; Na primer:

2 + 9 * (5 + 2³ - 24 ÷ 6) - 1

= 2 + 9 * (5 + 8 - 4) - 1

= 2 + 9 * 9 - 1

= 2 + 81 - 1

= 82.

V nekaterih izrazih se uporabljajo združevanje simbolov znotraj drugih, na primer, kadar je treba spremeniti znak operacije. V teh primerih se mora začeti z reševanjem od znotraj Out; to pomeni poenostavitev simbolov združevanja, ki so v središču izraza.

Na splošno je vrstni red reševanja operacij, ki jih vsebuje te simbole.

90 - 3_*[12 + (5_*4) - (4_*2)]

= 90 - 3_* [12 + 20 - 8]

Vam lahko služi: teoretična verjetnost: kako jo izvleči, primeri, vaje

= 90 - 3 _* 24. 24

= 90 - 72

= 18.

Vaje

Prva vaja

Poiščite vrednost naslednjega izraza:

dvajset² + √225 - 155 + 130.

Rešitev

Pri uporabi papomud je treba moči in korenine najprej rešiti in nato dodati in odštevati. V tem primeru prva dva operacija pripadata istemu vrstnemu redu, zato je ta, ki je najprej, rešena, začenši od leve proti desni:

dvajset² + √225 - 155 + 130

= 400 + 15 -155 + 130.

Nato dodajte in odštevanje, začenši tudi na levi:

400 + 15 -155 + 130

= 390.

Druga vaja

Poiščite vrednost naslednjega izraza:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)].

Rešitev

Začne se z reševanjem operacij, ki so znotraj oklepajev, po hierarhičnem vrstnem redu, ki ga imajo v skladu s Papomudami.

Najprej se rešijo pristojnosti prvega oklepaja, nato pa se rešijo operacije drugega oklepaja. Ko pripadajo istemu vrstnemu redu, je prvo delovanje izraza rešeno:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)]

= [- (216–729) ÷ (8 _* 6 ÷ 16)]

= [ - (216 - 729) ÷ (48 ÷ 16)]

= [- (-513) ÷ (3)].

Ker so operacije v oklepajih že rešene, se zdaj nadaljuje delitev, ki ima največjo hierarhijo:

[- (-513) ÷ (3)] = [- (-171)]].

Nazadnje oklepaja, ki loči znak minus (-) od rezultata, kar je v tem primeru negativno, kaže, da je treba pomnoževanje teh znakov narediti. Tako je rezultat izraza:

[- (-171)] = 171.

Tretja vaja

Poiščite vrednost naslednjega izraza:

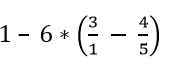
Rešitev

Frakcije, ki so znotraj oklepaja, so razrešene:

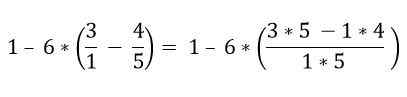
Znotraj oklepaja je več operacij. Množevanje se najprej rešijo in nato odštevanja; V tem primeru se frakcijska vrstica šteje za skupinski simbol in ne kot delitev, zato je treba reševati operacije zgornjega in spodnjega dela:

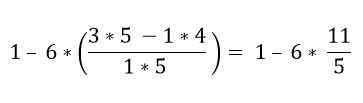
Po hierarhičnem vrstnem redu je treba rešiti množenje:

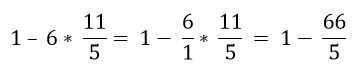
Končno je odštevanje rešeno: