Orthoedro formule, območje, prostornina, diagonala, primeri

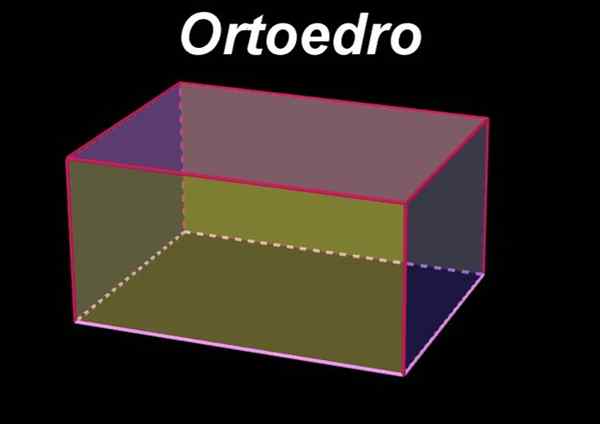
On Orthoedro Gre za volumetrično ali tridimenzionalno geometrijsko figuro, za katero je značilno šest pravokotnih obrazov, tako da so nasprotni obrazi v vzporednih ravninah in so enaki ali skladni pravokotniki med seboj. Po drugi strani so obrazi, ki mejijo na določen obraz.

Lahko tudi upoštevamo, kdaj Orthoedro kot pravokotna pravokotna osnovna prizma, v kateri Dihedrosovi koti Oblikovani z dvema načrti, ki mejijo na skupni rob, merijo 90 °. Dvostranski kot med dvema obrazoma se meri na presečišču obrazov s pravokotno in skupno ravnino do njih.

Slika 1. Orthoedro. Vir: f. Zapata z geogebro.

Prav tako je ortoedro a Pravokotnik vzporedno, Ker je to opredeljeno na vzporednici kot volumetrična figura šestih obrazov, ki sta vzporedna dva do dva.

V kateri koli vzporednici so obrazi paralelogrami, toda v pravokotniku, vzporedni, morajo biti obrazi pravokotni.

[TOC]

Deli ortoedro

Deli poliedra, kot je ortoedro, so:

-Robovi

-Točke 

-Obraze

Kot med dvema roboma obraza ortoedra sovpada z dihedrskim kotom, ki ga tvorita druga dva obraza, ki meji na vsakega od robov, in tvori desni kot. Naslednja slika pojasnjuje vsak koncept:

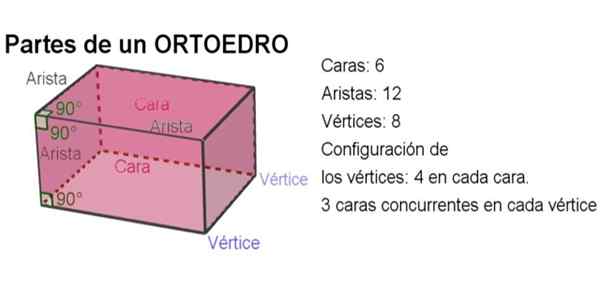Slika 2. Deli ortoedro. Vir: f. Zapata z geogebro.

-Skupaj ima ortoedro 6 obrazov, 12 robov in 8 vrhov.

-Kot med dvema roboma je pravi kot.

-Dvostranski kot med dvema stranicama je prav tako raven.

-V vsakem obrazu so štiri točke in v vsaki točki se udeležijo trije medsebojno pravokotni obrazi.

Vam lahko služi: kaj je številka capicúa? Lastnosti in primeri

Orthoedro formule

Območje

Površina ali površina a Orthoedro To je vsota območij njihovih obrazov.

Če imajo trije robovi, ki se strinjajo v točki C⋅B In obraz v ozadju ima tudi območje C⋅B.

Nato imata dva stranska obraza območje A⋅B vsak. In končno, obrazi tal in streha imata območje A⋅c vsak.

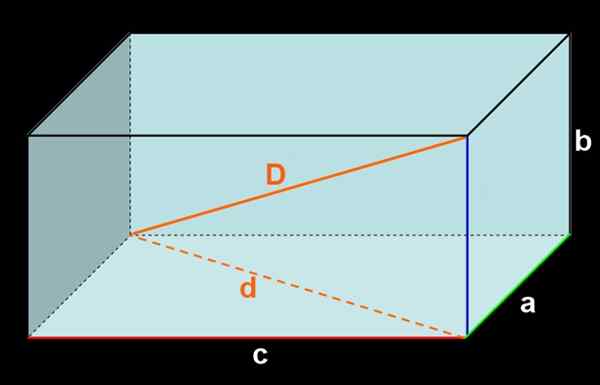Slika 3. Orthoedro dimenzij A, B, C. Notranja diagonala d in zunanja diagonala d.

Dodajanje območja vseh obrazov se dobi:

A = 2⋅C⋅B + 2⋅A⋅B + 2⋅A

Risanje skupnega faktorja in naročanje izrazov:

A = 2⋅ (A⋅B + B⋅C + C⋅A)

Glasnost

Če se orthoedro šteje za prizmo, se njen obseg izračuna na naslednji način:

Zvezek = osnovno območje prizme x Višina prizme

V tem primeru se tla dimenzij jemljejo kot pravokotna c in do, Torej je osnovno območje C⋅A.

Višino daje dolžina b Od pravokotnih robov do strani do in c.

Pomnoži osnovno območje (A⋅c) po višini b Imate glasnost V Iz ortoedro:

V = a⋅B⋅C

Notranja diagonala

V ortoedru sta dve vrsti diagonalov: zunanje diagonale in notranje diagonale.

Zunanje diagonale so na pravokotnih obrazih, notranje diagonale pa so segmenti, ki se pridružijo dve nasprotni točki, ki jih razumejo nasprotni točki, ki ne delijo nobenega roba.

V ortoedro so štiri notranje diagonale, vse enake ukrepe. Dolžina notranjih diagonalov lahko dobimo z uporabo teorema pitagore za pravokotnike.

Lahko vam služi: trigonometrične funkcije: Osnovne, v kartezijanski ravnini, primeri, vadba

Dolžina D zunanje diagonale ortoedre nadstropje izpolnjuje pitagorejsko razmerje:

d² = a² + c²

Podobno je diagonala merjenja notranjega merjenja pitagorejskega odnosa:

D² = d² + b².

Združitev dveh prejšnjih izrazov, ki jih imate:

D² = a² + c² + b².

Končno je dolžina katere koli notranje diagonale ortoedro podana z naslednjo formulo:

D = √ (a² + b² + c² ). 

Primeri

- Primer 1

Mason zgradi rezervoar v obliki ortoedro, katerega notranje dimenzije so: 6 m x 4 m baza in visoka 2 m. Zahteva se:

a) Določite notranjo površino rezervoarja, če je popolnoma odprta v zgornjem delu. 

b) Izračunajte prostornino notranjega prostora rezervoarja.

c) Poiščite dolžino notranje diagonale.

d) kakšna je zmogljivost rezervoarja v litrih?

Rešitev

Vzeli bomo dimenzije pravokotne osnove A = 4 m in c = 6 m in višino kot b = 2 m

Področje ortoedra z dimenzijami daje naslednje razmerje:

A = 2⋅ (A⋅B + B⋅C + C⋅A) = 2⋅ (4 m⋅2 m + 2 m⋅6 m + 6 m⋅4 m)

To pomeni:

A = 2⋅ (8 m² + 12 m² + 24 m²) = 2⋅ (44 m²) = 88 m²

Prejšnji rezultat je območje orthoedro, zaprtega z danimi dimenzijami, a ker je v zgornjem delu rezervoar, ki je popolnoma odkrit, da dobimo površino notranjih sten rezervoarja, območje manjkajočega pokrova to je:

C⋅a = 6 m ⋅ 4 m = 24 m².

Končno bo notranja površina rezervoarja: s = 88 m² - 24 m² = 64 m².

Rešitev b

Notranja prostornina rezervoarja je podana z prostornino ortoedro notranje dimenzije rezervoarja:

V = a⋅B⋅C = 4 m ⋅ 2 m ⋅ 6 m = 48 m³.

Rešitev c

Notranja diagonala oktaedra z dimenzijami notranjosti rezervoarja ima dolžino, ki jo daje:

Vam lahko služi: neprekinjena naključna spremenljivka

√ (a² + b² + c² ) = √ ((4 m)² + (2 m)² + (6 m)² )

Izvajanje navedenih operacij imamo:

D = √ (16 m² + 4 m² + 36 m² ) = √ (56 m²) = 2√ (14) M = 7,48 m.

Rešitev d

Za izračun zmogljivosti rezervoarja v litrih je treba vedeti, da je prostornina kubičnega decimetra enakovredna zmogljivosti litra. Prej je bil izračunan v volumnu v kubičnih metrih, vendar ga je treba spremeniti v kubične decimetre in nato v litre:

V = 48 m³ = 48 (10 dm)³ = 4.800 dm³ = 4.800 l

- Vaja 2

Stekleni akvarij ima kubično obliko 25 cm strani. Določite območje v m², Prostornina v litrih in dolžina notranje diagonale v CM.

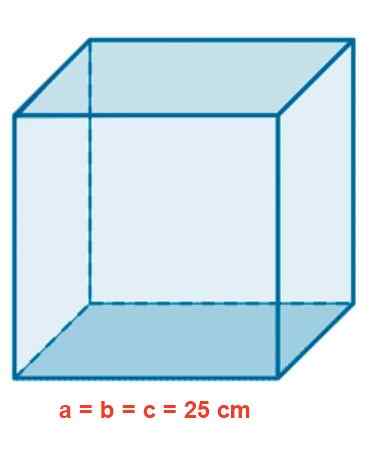Slika 4. Kubični stekleni akvarij.

Rešitev

Območje se izračuna z isto ortoedro formulo, vendar upoštevamo, da so vse dimenzije enake:

A = 2⋅ (3 a⋅A) = 6⋅ a² = 6⋅ (25 cm)² = 1.250 cm²

Obseg kocke je podan z:

V = a³ = (25 cm)³ = 15.625 cm³ = 15.625 (0,1 dm)³ = 15.625 dm³ = 15.625 l.

Dolžina d notranje diagonale je:

D = √ (3²) = 25√ (3) cm = 43,30 cm.

Reference

1. Arias J. Geogebra: Prizma. Obnovil od: YouTube.com.
2. Izračun.DC. Vaje in problemi, rešeni na območjih in količinah. Iztegnjeno od: izračun.DC.
3. Salvador r. Pyramid + Orthoedro z geogebro (IHM). Obnovil od: YouTube.com
4. Weisstein, Eric. "Ortoedro". Mathworld. Wolfram Research.
5. Wikipedija. Orthoedro. Okrevano od: je.Wikipedija.com