Matematika

Decimalna zapis

Decimalna zapis
3/2 delež, napisan v decimalni zapisi

Kaj je decimalna zapis?

The Decimalna zapis Sestavljen je iz pisanja resnične številke skozi celoten del in decimalni del, tako ločen s točko ali vejico. Celoten del je ostal in decimalni del desno od te točke.

0 se lahko pojavi tako v celotnem delu kot v decimalni. Na primer, naslednje številke so decimalne številke:

  • 0.25
  • 1.5903
  • 4.19367

Upoštevajte, da je decimalni del teh številk končen, vendar obstajajo tudi številke z neskončnim decimalnim delom, na primer 0,33333….

Na splošno je mogoče zapisati končno decimalno številko kot:

N.do1do2do3… Don

Ker je n in n in n količina decimalk, medtem ko neskončna decimalka sprejema obrazec:

N.do1do2do3..

V decimal 0.25 so identificirane:

  • N = 0
  • do1 = 2
  • do2 = 5

Decimali se pojavljajo kot drug način izražanja racionalnih števil, ki so oblikovane ali pokvarjene. Pravzaprav lahko kateri koli del zapišemo v decimalnem zapisu, kot bo razvidno takoj.

Služijo tudi za predstavljanje številk, ki ne izhajajo iz delčka, tako imenovane iracionalne številke, kot so: π, √2, √3, √5, število "e" in mnogi drugi.

Primeri decimalnih številk

Decimalno številko lahko dobimo iz del. Če je imenovalec enota, ki ji sledijo ničle, je to zelo preprosto:

  • 8/10 = 0.8
  • - (5/100) = −0.05

V prvem primeru, ker je imenovalec 10, se decimalna točka takoj postavi na levo od 8 in decimal.8 se glasi "8 desetin" ali "nič točke osem".

V drugem primeru, ker je imenovalec 100, morate decimalno točko postaviti dve mesti na levo od 5, in ker je število negativno, se glasi "manj 5 stotin" ali "manj nič nič točke pet".

Ko imenovalec ni enota, ki ji sledi 0, se uporablja dolga delitev:

Upoštevajte, da je za izvedbo te delitve, saj je števca manjši od imenovalca, pomnoženo najprej z 10 in pri tem je 0, ki ji sledi decimalna točka v količniku, da ne bi spremenili operacije, tako da ne Za spremembo operacije. Nato normalno nadaljujte, da razdelite 10 do 2, kar je enako 5, delitveni ostanek pa 0.

Vam lahko služi: vektorske količine

Decimalna oblika frakcije ½ je 0.5, tista "nič točka pet" se prebere:

Del 7/8 je še en primer. Ker je 7 manj kot 8, se pomnoži 7 × 10 = 70, v količniku je nameščen 0, ki mu sledi decimalna točka in je običajno razdeljena:

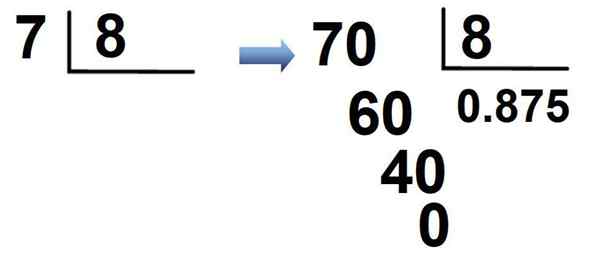
Rezultat tega je, da je del zapisan v decimalni zapisi kot:

7/8 = 0.875

Ta številka, tako kot prejšnji rezultat, je končna decimalka in način branja je: "Zero Point Osemsto sedemdeset -pet". S tem postopkom so v decimalni zapisi zapisane tudi naslednje frakcije:

8/10 = 0.8

5/7 = 0.714285714…

9/20 = 0.Štiri. Pet

3/8 = 0.375

Upoštevajte, da je kot v vseh teh frakcijah števca manjši od imenovalca, tudi celoten del nastalih decimalk je 0. Vendar mešana številka ali a Nepravilna frakcija (Da čigar števnik je večji od imenovalca) ima tudi decimalno zastopanje.

V tem primeru je celoten del večji ali enak 1, če je delež pozitiven in manjši od -1, če je negativen:

9/4 = 2.25

10/3 = 3.333333…

−12/5 = −2.4

1 ½ = 1.5

2 ¾ = 2.75

Celoten del in delni del negativnih decimalk

V prejšnjih primerih je bilo ugotovljeno, da se za iskanje decimalnega izražanja frakcije številčni in imenovalec preprosto razdelijo. Tudi če je frakcija negativna, je preprosto znamenje minus v enakovredni decimimientni izraz.

Vendar se celoten del in delni del decimalke razlikujeta glede na znak, ki ga nosite.

Ko je decimalka pozitivna, kot 2.25, celoten del je 2 in njen decimalni del je 0.25 in številko lahko zapišemo kot vsoto celotnega dela in decimalnega dela, kot je ta:

2.25 = 2 + 0.25

Celoten del je opredeljen kot celo število, ki je takoj nižje od decimalne in decimalni del je vedno pozitiven. Za 2.25, takoj nižje celo število je 2.

Toda v primeru frakcije −12/5, enakovredno decimalnim −2.4 Zgornje ne deluje.

Vam lahko služi: kakšni so deli kartezijanske ravnine?

 Če −2 je bil celoten del in 0.4 Decimalni del, z dodajanjem bi bil pridobljen:

−2 + 0.4 = −1.6 ≠ −2.4

Zato je celoten del −2.4 ne more biti −2, ampak takoj nižje celo število: −3. Toda v tem primeru delni del ne bi bil 0.4, saj z dodajanjem:

−3 + 0.4 = −2.6 ≠ −2.4

Torej, kakšen je decimalni del negativne številke −2.4? Odšteva decimalno številko od celotnega dela in rezultat bo vedno pozitiven:

−2.4 - ( - 3) = 0.6

Končno je dokazano, da se z dodajanjem celotnega dela in delnega dela pridobi iskana decimalna:

−3 + 0.6 = −2.4

Postopek za iskanje celega dela in decimalnega dela katere koli številke, ne glede na znak, je povzet na ta način:

  • Celoten del je celo število nižje od decimalnega števila.
  • Decimalni del se izračuna tako, da decimalno odštejemo od celotnega dela.

Vendar pa za praktične izračune decimalno število −2.4 je mogoče razčleniti kot - (2 + 0.4) = - 24/10 ali:

Kot je razvidno, decimalna zapisovalna predstavitev števila ni edinstvena.

Vrste decimalk

Obstajajo decimalne številke, katerih decimalni del je končen ali neskončen, ki se uporablja kot klasifikacijska merila:

Končni ali natančni decimali

Ko so decimali končni, na primer 0.125, pravijo tudi, da so natančne decimale.

Neskončni decimali

Neskončna decimalka dobimo, ko ostanek delitve med števcem in imenovalcem ni nikoli narejen 0.

Pod pogojem, da decimalka izvira iz količnika med dvema številoma, je ta decimalni del periodičen, torej je sestavljen iz ene ali več številk, ki se ponavljajo v nedogled obdobje.

Na primer številka 3.333333… nastaja nepravilna frakcija 10/3, je periodična decimalna: celoten del je 3, po decimalni točki. To je mogoče simbolizirati tako, da na številko, ki se ponovi, postavite krivuljo ali klobuk:

Obdobje je lahko večja številka, kot v frakciji 5/7, katerega predstavitev v decimalni zapisi je 0.71428571428571428… in napisano je kot:

Vam lahko služi: proporcionalna variacija

Te decimale, v katerih se obdobje pojavi takoj po decimalni točki Čiste periodične decimale. Vendar v tem drugem:

Obdobje, ki je 45, velja dve števki, ki se v decimalnem delu ne ponavljajo več: 23. Ta številka se imenuje predhodno obdobje, Ker je pred obdobjem. V tem primeru je Mešani časopis Decimal.

Končno obstajajo neskončni decimali, ki niso časopisi, ki ne izvirajo iz količnika med dvema celotnima številkama. Kot smo že omenili na začetku, ti decimali pripadajo celoti iracionalne številke, Kot na primer številka PI.

Rešene vaje

Vaja 1

Napišite številčne naslednje decimalne številke:

a) nič točka štiristo štirideset -seven
b) pet tisoč
c) dve enoti in pet stotin
d) tri točke sedemindvajset negativnih
e) Ena točka osemsto dvajset tisoč petsto šestdeset let

  • Rešitev

a) 0.447

b) 0.005

c) 2.05

d) −3.27

e) 1.824563

Vaja 2

Naslednje decimalne številke razvrstite v natančne decimalne, čiste časopise, mešane časopise ali iracionalne številke. V vseh primerih navedite vrednost celotnega dela in če so časopisi ali mešani časopisi, tudi navajajo vrednost obdobja in spredaj, kot je primerno:

a) 0.35627

b) 1.21212121…

c) −1.32

d) 1.414213562… = √2

  • Rešitev

a) 35627 je natančna decimalna. Celoten del je 0, njegov decimalni del pa je 0.35627.

b) 1.21212121… je neskončen decimalni in čisti časopis, celoten del je 1 in obdobje je 21.

c) −1.32 je natančna in negativna decimalna, katere celoten del je −2. Decimalni del se izračuna tako, da decimalno številko odštejemo od celotnega dela:

−1.32 - (−2) = 0.68

d) decimalni izraz √2 je neskončen in ni periodičen, saj je iracionalno število.

Je mešan časopis, celoten del je 3, sprednja je 1, obdobje pa 89.

Reference

  1. Pedagoški prispevki in didaktični material. Decimalna zapis. Okrevano od: tecdigital.Tec.AC.Cr.
  2. Baldor, a. 2007. Praktična teoretična aritmetika. Uredniška skupina Patria S.Do. od c.V.
  3. Matematika za trgovine. Razumevanje decimalne zapise. Pridobljeno iz: OpenTextbc.AC.
  4. Ne. Racionalne številke: pomeni in reprezentacije. Okrevano od: Redi.Kodoik.Ne.mx.