Lastnosti, primeri in operacije racionalnih številk

The racionalne številke So vse številke, ki jih je mogoče dobiti kot delitev dveh celotnih številk. Primeri racionalnih števil so: 3/4, 8/5, -16/3 in tisti, ki se pojavijo na naslednji sliki. V racionalnem številu je naveden količnik, ki ga je mogoče storiti pozneje, če je potrebno.

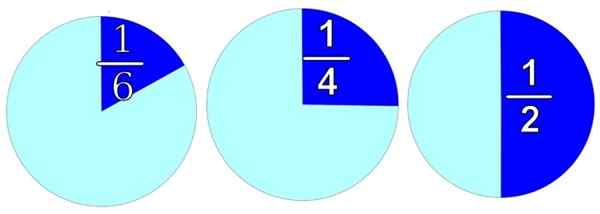
Na sliki je predstavljen kateri koli predmet, okrogel za udobje. Če ga želimo razdeliti na dva enaka dela, kot na desni, imamo dve polovici in vsaka je 1/2.

Slika 1. Racionalne številke se uporabljajo za delitev celote na različne dele. Vir: Freesvg.

Če ga delimo na 4 enake dele, bomo dobili 4 kose in vsak je vreden 1/4, kot na sliki središča. In če ga morate razdeliti v 6 enakih delih, bi bil vsak del vreden 1/6, kar vidimo na sliki na levi strani.

Seveda bi ga lahko razdelili tudi na dva neenakomerna dela, na primer, lahko obdržimo 3/4 delov in shranimo 1/4 dela. Možni so tudi drugi oddelki, na primer 4/6 in 2 dela. Pomembno je, da je vsota vseh delov 1.

Na ta način je razvidno, da lahko z racionalnimi številkami razdelite, štejete in distribuirate stvari, kot so hrana, denar, zemlja in vse vrste predmetov v ulomkih. In tako se količina operacij, ki jih je mogoče izvesti s številkami.

Racionalne številke je mogoče izraziti tudi decimalno, kot je razvidno iz naslednjih primerov:

1/2 = 0,5

1/3 = 0,3333…

3/4 = 0,75

1/7 = 0,142857142857142857…

Kasneje navedemo, kako prehoditi z ene poti na drugo s primeri.

[TOC]

Lastnosti racionalnih številk

Racionalne številke, katerih nastavimo s črko Q, imajo naslednje lastnosti:

-Q Vključuje naravne številke n in celotne N številke.

Ob upoštevanju katere koli številke do Lahko se izraža kot količnik drug z drugim in 1, enostavno je videti, da obstajajo tudi naravne številke in cela števila.

Tako lahko naravno številko 3 zapišemo kot delček in tudi -5:

3 = 3/1

-5 = -5/1 = 5/-1 = -(5/1)

Na ta način je številčni niz, ki pokriva večje število številk, nekaj zelo potrebnega, če "okrogle" številke niso dovolj, da bi opisali vse možne operacije.

Vam lahko služi: 90 delitev: kaj so in razlaga

-Lahko dodamo racionalne številke, odštejemo, množimo in delimo, rezultat operacije pa je racionalno število: 1/2 + 1/5 = 7/10; 1/2 - 1/5 = 3/10; (1/2) x (1/5) = 1/10; (1/2) ÷ (1/5) = 5/2.

-Med vsakim parom racionalnih številk je vedno mogoče najti drugo racionalno številko. Pravzaprav med dvema racionalnima številoma sta racionalni neskončni. 

Na primer, med racionalnimi 1/4 in 1/2 so racionalni 3/10, 7/20, 2/5 (in še veliko več), kar je mogoče preveriti, da jih izražajo kot decimalke.

-Vsako racionalno število lahko izrazimo kot: i) celo število ali ii) omejeno decimalno (strogo) ali časopis: 4/2 = 2; 1/4 = 0,25; 1/6 = 0,1666666…

-Enako število lahko predstavljajo neskončne enakovredne frakcije in vsi pripadajo Q. Poglejmo to skupino:

Vsi predstavljajo decimal 0.428571 ..

-Med vsemi enakovrednimi frakcijami, ki predstavljajo isto število, je nereducibilna frakcija, najpreprostejša od vseh, Kanonični predstavnik te številke. Kanonični predstavnik prejšnjega primera je 3/7.

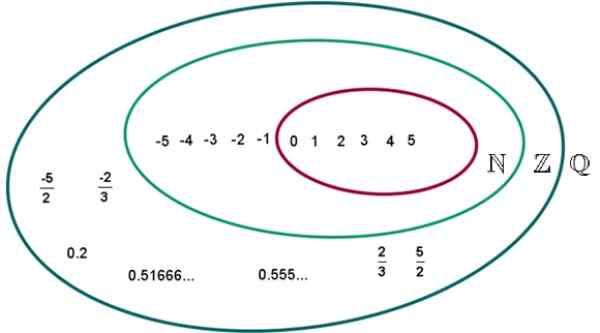Slika 2.- Q nabor racionalnih številk. Vir: Wikimedia Commons. UVM Eduardo Artur/CC by-S (https: // createCommons.Org/licence/by-sa/4.0.

Primeri racionalnih številk

-Lastne frakcije, tiste, v katerih je števec manj kot imenovalec:

-Nepravilne frakcije, katerih števec je večji od imenovalca:

-Naravne in cele številke:

-Enakovredne frakcije:

Decimalna reprezentacija racionalnega števila

Ko je števec razdeljen med imenovalec, je decimalna oblika racionalnega števila. Na primer:

2/5 = 0.4

3/8 = 0.375

1/9 = 0.11111 ..

6/11 = 0.545454…

V prvih dveh primerih je količina decimalk omejena. To pomeni, da se ob izdelavi delitve dobi počitek.

Po drugi strani je v naslednjih dveh število decimalcev neskončno in zato so postavljene suspenzivne točke. V slednjem primeru je v decimali vzorec. V primeru frakcije 1/9 se slika 1 ponavlja v nedogled, medtem ko je v 6/11 54.

Lahko vam služi: verjetnost frekvence: koncept, kako se izračuna in primeri

Ko se to zgodi, je rečeno, da je decimalna časopis časopis in jo označuje naglasni naglas Circumflex na naslednji način:

Preoblikujte decimal v frakcijo

Če je omejena decimalka, se vejica preprosto odpravi in ​​imenovalec postane enota, ki ji sledi toliko ničle, kolikor ima številke. Na primer preoblikovati decimal 1.26 v deli je napisano tako:

1.26 = 126/100

Potem je nastali delež poenostavljen do največjega:

126/100 = 63/50

Če je decimal neomejeno najprej, je obdobje ugotovljeno. Nato sledimo tem korakom, da bi našli nastalo frakcijo:

-Števec je odštevanje med številko (brez kome ali naglasa Corcusflex) in delom, ki ne vsebuje naglasa Courceflex.

-Imenovalec je celo število s toliko 9 kot številke, ki so tam pod okrožjem, in toliko ali kot številke v decimalnem delu.

Sledite temu postopku za preoblikovanje decimalne številke 0,428428428… v frakciji.

-Najprej je identificirano obdobje, ki je ponovljeno zaporedje: 428.

-Nato je narejeno delovanje odštevanja številke brez kome ali naglasa: 0428 dela, ki nima obrobja, kar je 0. To je 428 - 0 = 428.

-Imenovalec je zgrajen, saj ve, da so pod Circumflexom 3 številke in vsi so pod Circusflexom. Zato je imenovalec 999.

-Končno se frakcija oblikuje in poenostavlja, če je mogoče:

0.428 = 428/999

Ni mogoče več poenostaviti.

Delovanje racionalnih številk

- Dodati in odštevati

Frakcije z istim imenovalcem

Ko imajo frakcije enakega imenovalca, jih dodajte in/ali odštejte zelo enostavno, saj se števci preprosto dodajo algebraično, pri čemer se kot imenovalec rezultata pustijo enakemu dodatkom. Končno, če je mogoče, je poenostavljeno.

Primer

Izvedite naslednjo algebrsko vsoto in poenostavite rezultat:

Nastala frakcija je že nepopustljiva.

Frakcije z različnim imenovalcem

V tem primeru se dodatke nadomestijo z enakovrednimi ulomki z istim imenovalcem in nato je postopek že opisan. 

Primer

Algebraično dodajte naslednje racionalne številke, ki poenostavijo rezultat:

Vam lahko služi: robovi kocke

Koraki so:

-Določite minimalno skupno večkratno (MCM) imenovalcev 5, 8 in 3:

MCM (5,8,3) = 120

To bo imenovalec nastalega uloma, ne da bi poenostavili.

-Za vsak delež: MCM razdelite med imenovalca in pomnožite s števcem. Rezultat te operacije je postavljen z ustreznim znakom v števca frakcije. Na ta način dobimo delček, ki ustreza izvirniku, vendar z MCM kot imenovalec.

Na primer, za prvo frakcijo je števca zgrajena takole: (120/5) x 4 = 96 in dobimo:

Nadaljujte na enak način za preostale frakcije:

Končno se enakovredne frakcije nadomestijo, ne da bi pozabili na njihov znak in je narejena algebrska vsota števcev:

(4/5) + (14/8) - (11/3) + 2 = (96/120) + (210/120) - (440/120) + (240/120) =

= (96+210-440+24) / 120 = -110 / 120 = -11/12

- Množenje in delitev

Pomnoževanje in delitev se opravita po spodnjih pravilih:

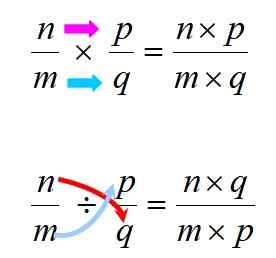Slika 3. Pravila za izvajanje množenja in delitve racionalnih številk. Vir: f. Zapata.

Vsekakor je pomembno, da se spomnimo, da je množenje komutativno, kar pomeni, da vrstni red dejavnikov ne spremeni izdelka. To se ne zgodi z oddelkom, zato morate paziti, da spoštujete odredbo med dividendo in delitvijo.

Primer 1

Izvedite naslednje operacije in poenostavite rezultat:

a) (5/3) x (8/15)

b) (-4/5) ÷ (2/9)

Odgovor na

(5/3) x (8/15) = (5 x 8)/(3 x 15) = 15/120 = 1/8

Odgovor b

(-4/5) ÷ (2/9) = (-4 x 9)/(5 x 2) = -36/10 = -18/5

Primer 2     

Luisa je imela 45 dolarjev. Deseto je kupil knjigo in 2/5 delov tistega, kar je ostalo v majici. Koliko denarja je ostalo Luisa? Izrazite rezultat v nerazrešljivi frakciji.

Rešitev

Stroški knjige (1/10) x 45 $ = 0.1 x 45 $ = 4.5 $

Zato je Luisa ostala pri:

45 - 4.5 $ = 40.5 $

S tem denarjem je Luisa odšla v trgovino z oblačili in kupila majico, katere cena je:

(2/5) x 40.5 $ = 16.2 $

Zdaj ima Luisa v portfelju:

40.5 - 16.2 $ = 24.3 $

Če ga želite izraziti v deli, je napisano tako:

24. 24.3 = 243/10

To je nepredelano.

Reference

1. Baldor, a. 1986. Aritmetika. Codex izdaje in distribucije.
2. Carena, m. 2019. Priročnik za matematiko. Nacionalna univerza na obali.
3. Figuera, j. 2000. Matematika 8. Co-Bo izdaje.
4. Jiménez, r. 2008. Algebra. Dvorana Prentice.
5. Racionalne številke. Okreval od: cimanet.UOC.Edu.
6. Racionalne številke. Pridobljeno od: webdelprofesor.Ula.pojdi.