Zgodovina iracionalnih številk, lastnosti, klasifikacija, primeri

The iracionalne številke To so tisti, katerih decimalni izraz ima neskončne številke brez ponavljajočega se vzorca, zato jih ni mogoče dobiti z izdelavo količnika med dvema številoma.

Med najbolj znanimi iracionalnimi številkami so:

Slika 1. Od zgoraj navzdol naslednje iracionalne številke: PI, število Eulerja, aúrea in dve kvadratni korenini. Vir: Pixabay.

Med njimi je brez dvoma π (pi) najbolj znan, vendar jih je še veliko več. Vsi pripadajo naboru resničnih števil, ki je številčni niz, ki združuje racionalne in iracionalne številke.

Spustne točke na sliki 1 kažejo, da decimali sledijo v nedogled, kar se zgodi, je, da prostor trenutnih kalkulatorjev omogoča le pokazati nekaj.

Če pogledamo natančno, pod pogojem, da naredimo količnik med dvema cestnimi celicami, dobimo decimalko z omejenimi številkami ali če ne, z neskončnimi številkami, v katerih se eno ali več ponavljajo. No, to se ne zgodi z iracionalnimi številkami.

[TOC]

Zgodovina iracionalnih številk

Veliki matematik antike pitagore, rojen leta 582.C v Samosu v Grčiji je ustanovil pitagoško miselno šolo in odkril znamenito izrek, ki nosi njegovo ime. Imamo ga navzdol na levi (Babilonci so ga že lahko poznali že veliko prej).

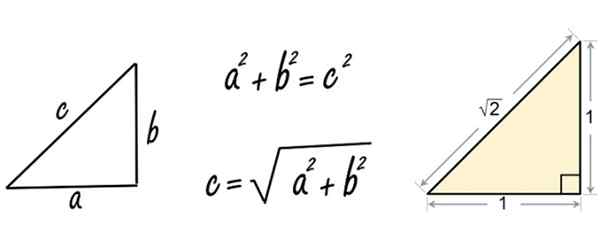Slika 2. Teorem Pythagora, ki se nanaša na trikotnik strani, enak 1. Vir: Pixabay/Wikimedia Commons.

No, ko je pitagora (ali verjetno njegov učenec) nanesel teorem na desni trikotnik, ki je enak 1, je našel iracionalno število √2.

Lahko vam služi: sušilne črte

To je storil tako:

C = √1² + 1² = √1+1 = √2

In takoj je spoznal, da ta nova številka ne izvira iz količnika med dvema naravnima številkama, ki sta bila tiste, ki sta bila takrat znana.

Zato ga je poklical iracionalno, In odkritje je povzročilo veliko tesnobo in zmedo med Pitagorejci.

Lastnosti iracionalnih številk

-Nabor vseh iracionalnih številk je označen s črko I in včasih kot Q* ali Q^C. Zveza med iracionalnimi številkami I ali Q* in racionalnimi številkami Q, povzroči niz resničnih N številk.

-Z iracionalnimi številkami je mogoče izvesti znane aritmetične operacije: vsota, odštevanje, množenje, delitev, potenciranje in drugo.

-Delitev med 0 ni opredeljena med iracionalnimi številkami.

-Vsota in izdelek med iracionalnimi številkami ni nujno drugo iracionalno število. Na primer:

√2 x √8 = √16 = 4

In 4 ni iracionalna številka.

-Vendar vsota racionalnega števila plus iracionalna povzroči iracionalno. Na ta način:

1 + √2 = 2.41421356237…

-Produkt drugačne racionalne številke od 0 po iracionalnem številu je tudi neracionalen. Poglejmo ta primer:

2 x √2 = 2.828427125…

-Inverzno iracionalno rezultat v drugem iracionalnem številu. Poskusimo nekaj:

1 / √2 = 0.707106781…

1 / √3 = 0.577350269…

Te številke so zanimive, ker so tudi vrednosti nekaterih trigonometričnih razlogov znanih zornih kotov. Večina trigonometričnih razlogov je iracionalna številka, vendar obstajajo izjeme, na primer Sen 30 ° = 0.5 = ½, kar je racionalno.

-V skupni vlogi so izpolnjene komutacijske in asociativne lastnosti. Če sta A in B dve neracionalni številki, to pomeni, da:

Lahko vam služi: Prevelika funkcija: definicija, lastnosti, primeri

A + b = b + a.

In če je C še ena iracionalna številka, potem:

(A + b) + c = a + (b + c).

-Distribucijska lastnost množenja glede na vsoto je še ena znana lastnost, ki je izpolnjena tudi za iracionalne številke. V tem primeru:

do.(B+C) = a.b + a.c.

-Iracionalno, da ima svoje nasprotje: -a. Ko je rezultat dodan, je 0:

A+(-a) = 0

-Med dvema različnima racionalnima je vsaj eno iracionalno število.

Lokacija iracionalne številke na pravi črti

Prava črta je vodoravna črta, kjer se nahajajo resnične številke, od katerih so iracionalni pomemben del.

Če želite najti iracionalno številko na pravi črti, v geometrijski obliki, smo lahko vredni teorema Pitagore, pravila in kompasa.

Kot primer bomo poiskali √5 na pravi črti, za katero narišemo pravokotnik strani x = 2 in y = 1, Kot prikazuje slika:

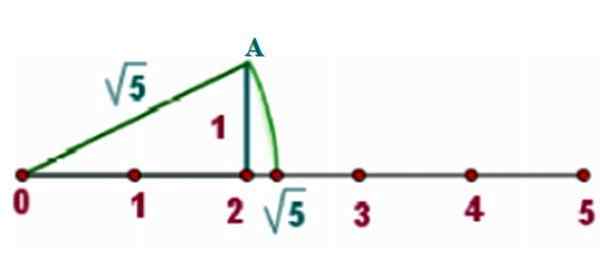Slika 3. Metoda za iskanje iracionalne številke na resnični liniji. Vir: f. Zapata.

Za teorem pitagore je hipotenuza takšnega trikotnika:

C = √2² + 1² = √4+1 = √5

Zdaj je utrip s konico postavljen na 0, kjer je tudi ena od vrst pravega trikotnika. Konica svinčnika kompasa mora biti na vrhovi do.

Narisan je obod, ki reže pravo črto. Ker je razdalja med središčem oboda in katero koli točko istega polmera, ki je vredna √5, je tudi križišče √5 od središča.

Grafa je razvidno, da je √5 med 2 in 2.5. Kalkulator nam ponuja približno vrednost:

Vam lahko služi: koeficient določanja: formule, izračun, razlaga, primeri

√5 = 2.236068

In tako je mogoče nastaviti trikotnik z ustreznimi stranicami, druge iracionalne, na primer √7 in drugi.

Razvrstitev iracionalnih številk

Iracionalne številke so razvrščene v dve skupini:

-Algebrski

-Transcendentna ali transcendentalna

Algebrske številke

Algebrske številke, ki so lahko neracionalne ali ne, so rešitve polinomnih enačb, katerih splošna oblika je:

do_n xⁿ + do_N-1x^N-1 + do_N-2x^N-2 +.. . +do₁x + a_tudi = 0

Primer polinomne enačbe je enačba druge stopnje, kot je ta:

x³ - 2x = 0

Enostavno je dokazati, da je iracionalna številka √2 ena od rešitev te enačbe.

Transcendentne številke

Namesto tega transcendentna številka, čeprav neracionalna, nikoli ne nastanejo kot rešitev polinomne enačbe.

Transcendentne številke, ki jih najpogosteje najdemo v uporabljeni matematiki, so π, za njun odnos z obodom in številko E ali Eulerjevo številko, kar je osnova neperijskih logaritmov.

Vaja

Na črnem kvadratu je postavljena siva v položaju, navedenem na sliki. Znano je, da je površina črnega kvadrata 64 cm². Koliko sta dolžini obeh kvadratov?

Slika 4. Dva kvadrata, od katerih je treba najti dolžino strani. Vir: f. Zapata.

Odgovor

Površina kvadrata stranske L je:

A = l²

Ker je črni kvadrat 64 cm² območja, mora biti njegova stran 8 cm.

Ta ukrep je enak kot Diagonala sivega kvadrata. Če uporabimo teorem pitagore na tej diagonali in se spomnimo, da so strani kvadrata enake, bomo imeli:

8² = L_g² + L_g²

Kjer l_g Je stran sivega kvadrata.

Zato: 2l_g² = 8²

Uporaba kvadratnega korena na obeh straneh enakosti:

L_g = (8/√2) cm

Reference

1. Carena, m. 2019. Priročnik za matematiko prednavdljivosti. Nacionalna univerza na obali.
2. Figuera, j. 2000. Matematika 9. Stopinja. Co-Bo izdaje.
3. Jiménez, r. 2008. Algebra. Dvorana Prentice.
4. Izobraževalni portal. Iracionalne številke in njihove lastnosti. Pridobljeno iz: portaledukcijsko.mreža.
5. Wikipedija. Iracionalne številke. Okrevano od: je.Wikipedija.org.