Liha števila

Kaj so nenavadne številke?

The liha števila So tiste celotne številke, ki jih 2 ni mogoče deliti 2. To pomeni, da z nenavadnimi količinami ne morete narediti skupin 2, na primer, če ima nekdo 9 bombonov, ki bi jih lahko delili s prijateljem in jih ne želite deliti, se bodo dotaknili 4 bombonov in ostalih 5.

Nekatere od lih številk so naslednje: ... -5, -3, -1, 1, 3, 5, 7, 9, 11, 13 ..  V tem izrazu SUSSIONSKE TOČKE kažejo, da je več številk, levo in desno.

Slika 1: Kako vedeti, ali je številka čudna?

Če pogledate previdno, lahko vidite, da lahko vsako liho številko dobite tako, da dodate 2 v prejšnjo številko. Na primer, če dodamo 2 v -1, dobite 1, če naredimo 1 + 2, je 3 in tako naprej.

Opažamo tudi, da če se pari prepletajo, vključno z 0, kar velja za enakomerno število, dobimo niz celih števil Z.

Zato je mogoče katero koli nenavadno naravno število zapisati v obliki 2n + 1, kjer je n = 0, ± 1, ± 2, ± 3, ± 4, ± 5…, kjer simbol ± pomeni, da ga je mogoče jemati kot pozitiven ali kot negativno.

V primeru večjih številk ga je mogoče prepoznati, ko je čudno, ker se vedno konča v 1, 3, 5, 7 ali 9. Na primer, 1571 je nenavadno in tako je tudi negativno celo število -152.489.

Primeri neparnih številk

Neparno številke so pogosto predstavljene v naravi, med njimi pa je številka 3 posebnega pomena. Poglejmo nekaj primerov:

-Obstaja veliko cvetov z lihom številom cvetnih listov.

-V vsaki roki imamo 5 prstov.

Vam lahko služi: naključna spremenljivka: koncept, vrste, primeri

-Človeška bitja imajo 23 kromosomov.

-Obstajajo trije zakoni Newtona in trije zakoni termodinamike.

-Jedra atomov, ki imajo neparno število protonov in nevtronov.

-Magiji so 3.

-V zgodbah in zgodbah se pogosto pojavlja številka 3, na primer romani, kot so Trije mušketirji avtor Alejandro Dumas in v priljubljenih zgodbah, kot so Trije bratje in Trije mali prašiči.

-Za umetniško skladbo je klic Nenavadno pravilo, ki določa, da je skladba z lihom številom elementov privlačnejša od enega s parom. Neparna številka dodaja dinamiko, en par pa stabilnost.

Slika 2. Neparno število elementov dodajo dinamiko na sliko

-Skupna strategija, da se cene predmetov zdijo cenejša, je, da končate 9, na primer 2.99 USD, 39 USD in tako naprej.

-Številka 13 nekateri štejejo za slabo srečo, drugi pa mistične lastnosti pripisujejo 11, obe neparni številki.

Primo številke

Primo številke, tiste, ki priznavajo samo kot delitve in 1, so nenavadne, z izjemo 2, ki je edini navor številke.

Možno je dokazati, da je mogoče katero koli število razčleniti kot produkt glavnih dejavnikov (vključno s temi pristojnostmi) in da je tak način izražanja številke edinstven, razen v vrstnem redu dejavnikov.

Na primer, številko 45 lahko razčlenimo kot 45 = 3³ x 5.

Operacije nenavadnih številk

Z neparnimi številkami se izvajajo vse aritmetične operacije, nekatere pa imajo izjemne značilnosti.

Vam lahko služi: simbolizacija izrazov

- Vsote in izdelki

-Vsota dveh neparnih številk povzroči enakomerno število: 3+5 = 8; 11+15 = 26; (-10)+ (+6) = - 4.

-Z dodajanjem neparne številke z enim navorom je rezultat nenavaden: 7+2 = 9; 26+ 9 = 35; (-5) + 12 = 7.

-Če n Prva naravna, nenavadna in zaporedna številka je rezultat n². Poglejmo to z malo več podrobnosti:

Za n = 2: 1 + 3 = 4 = 2²

Za n = 3: 1 + 3 + 5 = 9 = 3²

Za n = 4: 1 + 3 + 5 + 7 = 16 = 4²

-Ko se nepar pomnoži s parom, izvira enakomerno število: 7 x 4 = 28; (-3) x 12 = -36.

-Pomnoževanje dveh neparnih števil, dobimo tudi lih: 3 x 5 = 15; (-5) x (+11) = -55.

- Moči

-Ko se pozitivno število dvigne na nenavadno moč, je pozitivno število, na primer: 3³ = 27.

-Z dvigom negativne številke na nenavadno moč je rezultat negativen: (-2)³= (-2) x (-2) x (-2) = -8.

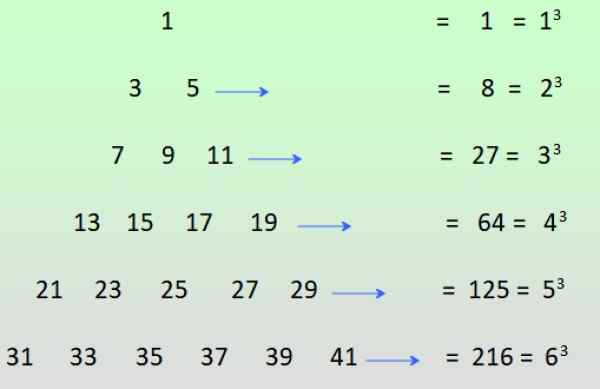
-Nenavadne moči pozitivnih celih števil je mogoče doseči, če so na voljo neparne številke, kot je prikazano na sliki in dodane vrstice:

Slika 3. Pridobivanje nenavadnih moči iz vsote lih številk. Vir: f. Zapata.

Rešene vaje

- Vaja 1

Odločite se, ali je rezultat naslednjega operacije enakomeren ali nenavaden:

(53476890083 + 1987628967) x 13567903

Rešitev

Če želite pridobiti odgovor, vam ni treba zagnati, da bi iskali kalkulator, ampak za uporabo vidnih lastnosti. Oglejmo si zadnje številke dodatkov, ki so 3 oziroma 7:

53476890083  + 1987628967

To pomeni, da so odvisniki čudni in že vemo, da je vsota dveh lih številk enakomerna.

Zato je številka, ki je posledica oklepaja, enakomerna in se bomo pomnožili za številko, ki se konča v 3:

Vam lahko služi: vektorska algebra

13567903

Kar pomeni, da je ta številka čudna.

V zgoraj opisanih lastnostih je bilo ugotovljeno, da je množenje navora x enakomerno število. Zato je nastala operacija enakomerna.

- Vaja 2

Koliko je vsota prvih 5 zaporednih neparnih številk? In prvih 50?

Rešitev

Vsota prvih 5 zaporednih neparnih števil je:

1 + 3 + 5 + 7 + 9 = 25

Če pa želimo dodati prvih 50 na ta način, je okorno, zato gremo na lastnosti. Potrjujejo, da je vsota zaporednih neparnih številk n². V tem primeru n = 50 in zahtevana vsota je:

petdeset² = 50 x 50 = 2500.

- Vaja 3

Ko se dodajo tri zaporedne neparne številke, dobimo 237. Kakšne so številke?

Rešitev

Poimenujmo svojo prvo nenavadno številko, drugi in Z pa tretji, v skladu z izjavo je izpolnjeno:

x + y + z = 237

V algebrskem jeziku lahko v obrazcu 2n +1 zapišete katero koli lirno številko. Naredimo našo prvo nenavadno številko:

x = 2n +1

Dodamo 2, da dobimo naslednje osebo:

y = x + 2 = (2n + 1) + 2 = 2n + 3

In končno je spet dodan 2, da dobimo tretjo liho:

Z = (2n +3) + 2 = 2n + 5

Vse to dodaja:

2n + 1 + 2n + 3 + 2n + 5 = 237

6n + 9 = 237

To ima za posledico preprosto linearno enačbo, katere rešitev je:

n = 38

In zdaj z vrednostjo n = 38 obstajajo tri naročila:

x = (2 × 38) + 1 = 77

Sledijo nedvomne zaporedne:

y = 79

Z = 81

In bralec zlahka preveri, ali je vsota treh 237.

Reference

1. Baldor, a. 1986. Aritmetika. Codex izdaje in distribucije.
2. Soseske, l. Neparne številke in moči naravnih številk. Pridobljeno od: sinewton.org.
3. Briljantno. Celo in neparne številke. Okreval od: briljantno.org.
4. Matematika 18. Operacije nenavadnih številk. Pridobljeno iz: matematika18.com.
5. Wikipedija. Celo in neparne številke. Okrevano od: je.Wikipedija.org.