Eulerjeva številka ali številka e, koliko je vredno, lastnosti, aplikacije

On Eulerjeva številka ali številka E To je dobro znana matematična konstanta, ki se pogosto pojavlja v številnih znanstvenih in ekonomskih aplikacijah, skupaj s številom π in drugimi pomembnimi številkami v matematiki.

Znanstveni kalkulator vrže naslednjo vrednost za številko E:

Slika 1. Eulerjeva številka se pogosto pojavlja v znanosti. Vir: f. Zapata.

E = 2.718281828…

Toda na primer je znanih še veliko decimalk:

E = 2.71828182845904523536…

In sodobni računalniki so do številke E omogočili decimalni trilijon.

To je številka iracionalno, kar pomeni, da ima neskončno količino decimalk brez kakršnega koli ponavljajočega se vzorca (zaporedje 1828 se na začetku pojavi dvakrat in se ne ponovi več).

In to pomeni tudi, da številke E ni mogoče dobiti kot količnik dveh celotnih številk.

[TOC]

Zgodovina

Število in Znanstvenik Jacques Bernoulli ga je identificiral leta 1683, ko je preučeval problem sestavljenega zanimanja, prej pa se je posredno pojavil v delih škotskega matematika Johna Napierja, ki je izumil logaritme za 1618.

Vendar mu je Leonhard Euler leta 1727 dal ime številke E in intenzivno preučeval njegove lastnosti. Zato je znan tudi kot Eulerjeva številka in tudi kot naravna podlaga za neperijske logaritme (eksponent).

Koliko je vredna številka E?

Številka E Vale:

E = 2.71828182845904523536…

Suspenzivne točke pomenijo, da obstaja neskončna količina decimalk in v resnici jih milijoni znanih s trenutnimi računalniki.

Reprezentacije številke E

Obstaja več načinov za določitev E, ki jih opisujemo spodaj:

Številka E kot meja

Eden od različnih načinov, kako se izraža številka E, je tisti, ki ga je znanstvenik Bernoulli našel pri svojem delu na sestavljenem interesu:

V katerem morate narediti vrednost n Zelo veliko število.

S pomočjo kalkulatorja je enostavno preveriti, kdaj n Je zelo velik, prejšnji izraz se nagiba k vrednosti in dano zgoraj.

Lahko vam služi: bijjektivna funkcija: kaj je to, kako je to, primeri, vaje

Seveda se lahko vprašamo, kako veliko je mogoče storiti n, Tako poskusimo z okroglimi številkami, kot so na primer:

n = 1000; 10.000 ali 100.000

V prvem primeru dobite E = 2.7169239… . V drugem E = 2.7181459… in v tretjem je veliko bolj blizu vrednosti in: 2.7182682. To se lahko že zdimo z n = 1.000.000 ali večji, pristop bo še boljši.

V matematičnem jeziku, postopek izdelave n Se bliža in bolj zelo veliki vrednosti, imenuje se omejitev na neskončnost In je označeno tako:

Za označevanje neskončnosti se uporablja simbol "∞".

Številka E kot vsota

S to operacijo je mogoče določiti tudi številko E:

Številke, ki se pojavljajo v imenovalcu: 1, 2, 6, 24, 120 ... ustrezajo operaciji n!, kje:

n! = n. (N-1).(N-2). (N-3) ..

In po definiciji 0! = 1.

Enostavno je preveriti, ali več ko se dodajo dodatki, večja je dosežena številka in.

Naredimo nekaj testov s kalkulatorjem in dodamo vse pogostejše dodatke:

1 +1+ (1/2) + (1/6) = 2.71667

1 +1+ (1/2) + (1/6) + (1/24) = 2.75833

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) = 2.76667

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) + (1/720) = 2.71806

Več izrazov so dodani v znesek, bolj je rezultat podoben in.

Matematiki so za te vsote zasnovali kompaktni zapis, ki vključujejo številne izraze z uporabo simbola vsote σ:

Ta izraz se bere kot "vsota n = 0 do neskončnosti 1 med n faktorial".

Številka E z geometrijskega vidika

Številka E ima grafični prikaz, povezan z območjem pod grafom krivulje:

y = 1/x

Ko so vrednosti X med 1 in E, je to območje vredno 1, kot je prikazano na naslednji sliki:

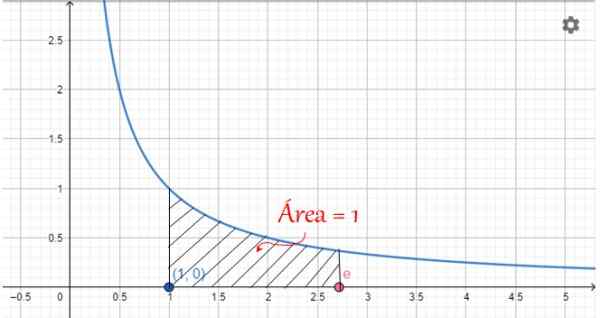Slika 2. Grafični prikaz številke E: Območje pod krivuljo 1/x, med x = 1 in x = e. Vir: f. Zapata.

Lastnosti številke E

Nekatere lastnosti številke E so:

Lahko vam služi: Graščanje funkcije: Kako jo prepoznati, primeri, vaje

-Z drugimi besedami je iracionalen, ni mogoče dobiti preprosto z delitvijo dveh celotnih številk.

-Število in Je tudi a Transcendentna številka, kar to pomeni in Ni rešitev nobene polinomne enačbe.

-Povezana je s štirimi drugimi znanimi številkami na področju matematike, in sicer: π, i, 1 in 0, skozi identiteto Eulerja:

in^πi + 1 = 0

-Klici zapletene številke se lahko izrazi z e.

-Je osnova naravnih ali neperijskih logaritmov danes (prvotna definicija Johna Napierja se nekoliko razlikuje).

-To je edina številka, tako da je njen neperijski logaritem vreden 1, to je:

 ln e = 1

Prijave

Statistika

Številka E se zelo pogosto pojavlja na področju verjetnosti in statistike, ki se pojavlja v različnih porazdelitvah, kot sta običajna ali Gaussova, številka Poissona in drugih.

Inženiring

Pri inženirstvu je pogosta, saj eksponentna funkcija y = e^x Na primer je prisoten v mehaniki in elektromagnetizmu. Med številnimi aplikacijami lahko navajamo:

-Kabel ali veriga, ki se visi na koncih, sprejme obliko krivulje, ki jo daje:

y = (e^x + in^-x) /2

-Kondenzator C je sprva izpuščen, ki se zaporedno povezuje z uporom R in napetostnim virom V za obremenitev, pridobi določeno obremenitev Q, odvisno od časa t, ki ga daje:

Q (t) = cv (1-e^-T/RC)

biologija

Eksponentna funkcija y = a.in^Bx, S konstanto A in B se uporablja za modeliranje rasti celic in rasti bakterij.

Fizično

V jedrski fiziki radioaktivno razpadanje in določitev starosti modeliramo z radiokarbonom.

Ekonomija

Pri izračunu sestavljenih interesov se število E nastaja naravno.

Recimo, da imate določeno količino denarja Str_tudi, investirati po letni obrestni meri.

Če denar ostane eno leto, boste po tem času imeli:

P (1 leto) = P_tudi + Str_tudi.i = p_tudi (1+ i)

Po drugem letu, ne da bi se ga dotaknili, boste imeli:

Vam lahko služi: teoretična verjetnost: kako jo izvleči, primeri, vaje

P (2 leti) = P_tudi + Str_tudi.i + (str_tudi + Str_tudi .i) i = P_tudi +2 p_tudi.i + p_tudi.Yo²  = PO (1+i)²

In na ta način n leta:

P = p_tudi (1+i)ⁿ

Zdaj se spomnite ene od definicij E:

Nekoliko izgleda kot izraz za p, zato mora obstajati odnos.

Razdelili bomo nominalno obrestno mero Yo v n Časovna obdobja, na ta način bo sestavljena obrestna mera I/N:

P = p_tudi [1+ (I/N)]ⁿ

Ta izraz je o naši meji malo bolj videti, vendar še ni povsem enak.

Vendar pa je po nekaterih algebrskih manipulacijah mogoče pokazati, da je ta sprememba spremenljivke:

h = n/i → i = n/h

Naš denar p postane:

P = p_tudi [1+ (1/h)]^Živjo = Str_tudi [1+ (1/h)]^hYo

In kaj je med tipkami, tudi če je napisano s pismom h, Je enak argumentu meje, ki definira številko E, manjka pa le za prevzem meje.

Naredimo  h → ∞ in tisto, kar je med tipkami, se spremeni v številko in. To ne pomeni, da moramo počakati neskončno velik čas, da umaknemo svoj denar.

Če smo videti dobro, ko to počnemo H = n/i In nagibanje k ∞, kar smo v resnici storili, je, da obrestno mero distribuiramo v zelo, zelo majhnih obdobjih: zelo majhno:

I = n/h

To se imenuje Neprekinjena kapitalizacija. V tem primeru se znesek denarja enostavno izračuna na naslednji način:

P = p_tudi .in^Yo

Kjer sem letna obrestna mera. Na primer, z deponiranjem od 12 do 9 % na leto z neprekinjeno kapitalizacijo po enem letu imate:

P = 12 x e^{0.09 × 1} € = 13.13 €

Z dobičkom 1.13 €.

Reference

1. Uživajte v matematiki. Sestavni interes: periodična sestava. Okrevano od: Uživajte.com.
2. Figuera, j. 2000. Matematika 1. Raznovrstno. Co-Bo izdaje.
3. Garcia, m. Številka E v osnovnem izračunu. Okrevano od: matematika.CIENS.UCV.pojdi.
4. Jiménez, r. 2008. Algebra. Dvorana Prentice.
5. Larson, r. 2010. Izračun spremenljivke. 9na. Izdaja. McGraw Hill.