Matematika

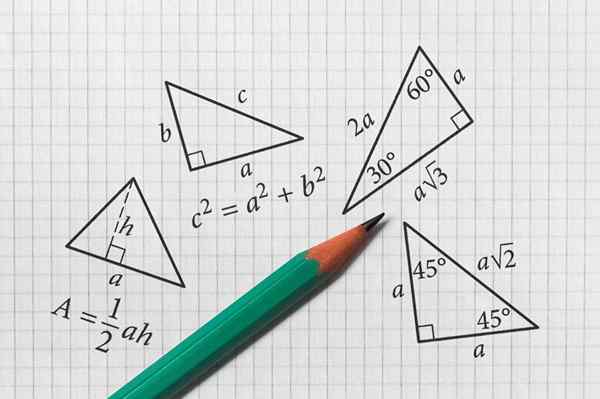
Koti in trikotniki

Koti in trikotniki
Koti in trikotniki so del ravne geometrije. Shuttersock

Kaj so koti in trikotniki?

A kot To je območje letala, ki ga je dva polčasnik, ki ima skupno izvorno točko. Ta točka je znana kot Vertex, Medtem ko se kličejo pol -utrip strani. Po drugi strani pa a Trikotnik Gre.

Najprej se bomo pogovarjali o kotih.

Koti

Obstaja več načinov za označevanje kotov: z grškimi črkami, kot so α, β, γ, ki jim lahko dodamo naglas obkrožanja; z velikimi črkami oblazinjene ali male črke, A, B, C, A, B, C; številke, na primer 1, 2, 3 ... ali uporaba simbola kota ∠.

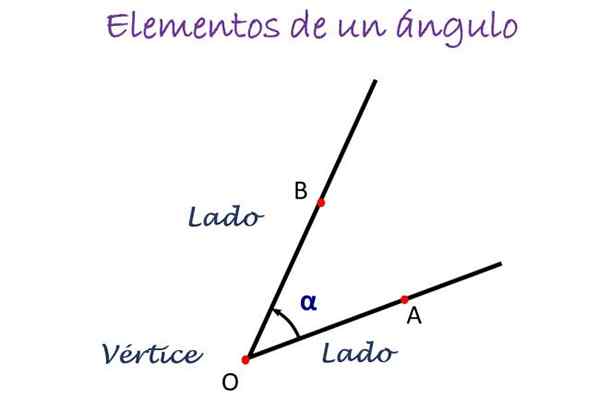Glavni elementi kota. Vir: f. Zapata

Na zgornji sliki se kot se meri od strani A do B, označen s smerjo puščice, na sredini pa je črka, ki označuje točko. Kot je nato označen kot ∠ aob.

Ko se kot meri v antihorarijskem smislu, se a +znak avovorično dodeljuje in če se meri v urniku.

Ukrep kotov se izvaja s prevoznikom, ki je sestavljen iz polkrožne plastične pločevine, kot je tisti, prikazan spodaj. Polkrog je razdeljen na 180 enakih delov, vsak klic stopinja.

Za merjenje je vrha kota sovpada z osrednjo točko transporterja, označeno s puščico, in začetno stranjo z enim od robov, notranjih ali zunanjih. Končna stran seka nekatere oznake transporterja, pri čemer je ta ukrep kot.

Vam lahko služi: empirično pravilo: kako ga uporabiti, za kaj je, rešene vaje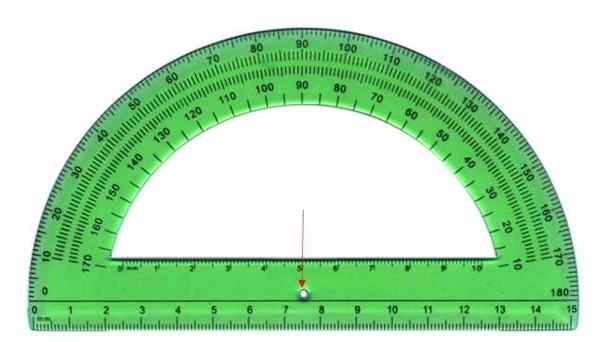Transporter je instrument za merjenje kotov. Vir: Wikimedia Commons

Vrste kotov

Eno najbolj uporabljenih meril za razvrščanje kotov je v skladu z njegovim ukrepom. Zato je lahko kot:

  • Nič, Ukrepi 0 °.
  • Ostro, katerega ukrep je med 0 in 90 °.
  • Naravnost, Meri natančno 90 °.
  • Obtuse, Je večji od 90 ° in manj kot 180 °.
  • Stanovanje, Njen ukrep je enak 180 °.
  • Dokončati, predstavlja popoln zavoj in meri 360 °.
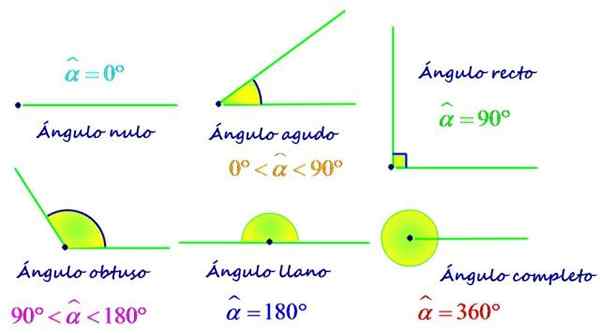Vrste kotov glede na vaš ukrep. Vir: f. Zapata.

Glede na razmerje med njegovim ukrepom in ravnim kotom, ki je 180 °, lahko kote razvrstimo tudi kot:

  • Konkavno, Če meri manj kot 180 °. Zato so akutni, ravni in obtujeni koti konkavni, saj je njegov ukrep vedno manjši od 180 ° (glej zgornjo sliko).
  • Konveksna, Če je vaš ukrep večji od 180 °, kot koti 270 ° in 360 °.

Koti glede na vsoto njihovih ukrepov in glede na položaj njihovih strani

Dva kota ∠ A in ∠ B sta lahko:

  • Komplementarno, Če je vsota njegovih ukrepov enaka 90 °.
  • Dopolnilno, Pri dodajanju ustreznih ukrepov dobimo 180 °.
  • Konjugirano, Če je ta vsota enaka 360 °.
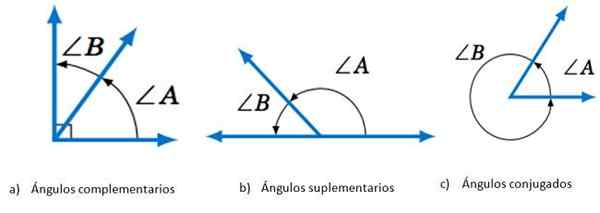Koti glede na vsoto njegovih ukrepov. Vir: matematika librettexts.

Kar zadeva položaj njihovih strani, sta lahko dva kota:

  • Zaporedoma, Ko imata skupna točka in ena od strani.
  • V bližini, Če so zaporedne, vendar so stranice, ki niso v nasprotju s.
  • Nasproti točke, Ko imajo skupno točko in se strani kotov podaljšajo v nasprotni smeri.
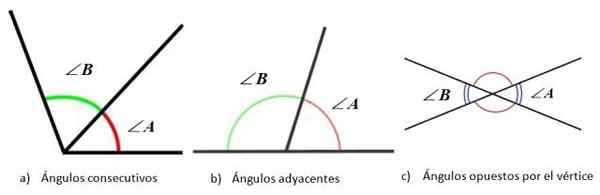Koti glede na relativni položaj med stranicami. Vir: f. Zapata

Trikotniki

Trikotnik je ravna in zaprta geometrijska figura, ki pripada družini poligonov, s tremi stranmi, sestavljenimi iz linij, ki so razrezane dve do dve, ustvarijo tri kote.

Lahko vam služi: bijjektivna funkcija: kaj je to, kako je to, primeri, vaje

Njeni osnovni elementi so:

  • Točke, ki so točke presečišča prej omenjenih linij.
  • Strani, Skupaj 3 in ki so sestavljene iz segmentov linij, ki se povezujejo z vrhovi.
  • Notranji koti, Tudi v številu 3, katerih vsota je vedno enaka 180 °.

Na splošno so stranice označene z malimi črkami latinskih črk, vrhovi z velikimi črkami in koti z malimi črkami, vendar so možni tudi drugi zapisi.

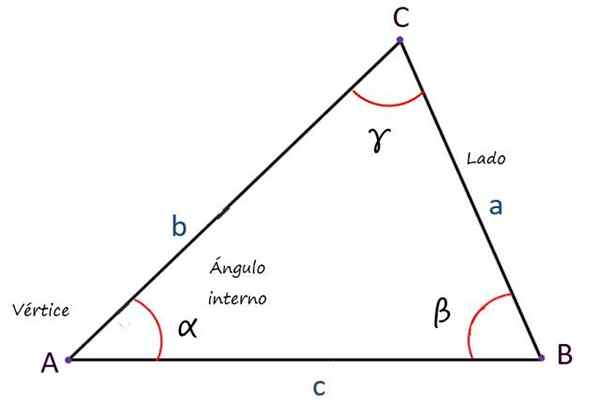Glavni elementi trikotnika. Vir: f. Zapata

Vrste trikotnikov

Trikotniki glede na obliko svojih strani

V skladu s tem kriterijem so lahko trikotniki:

  • Enakostranski, Če imajo tri strani enak ukrep.
  • Izosceles, Kadar imata samo dve strani enako mero, medtem ko je tretja drugačna.
  • Scalene, Če so tri strani različne velikosti.
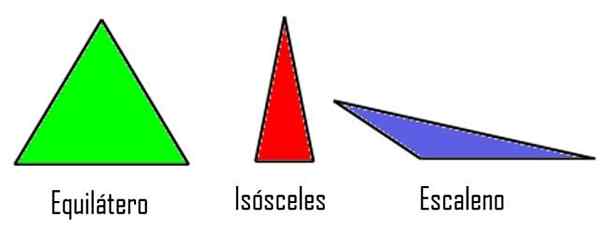Trikotniki glede na njihove strani. Spremenjeni Wikimedia Commons

Trikotniki glede na svoje notranje kote

To merilo temelji na notranjih kotnih vrstah trikotnika. V skladu s tem je lahko trikotnik:

  • Akutant, Ko so trije notranji koti trikotnika akutni.
  • Pravokotnik, Če ima trikotnik notranjega merskega kota, ki je enak 90 °.
  • Obtuse, Eden od notranjega kota trikotnika je prisrčen.
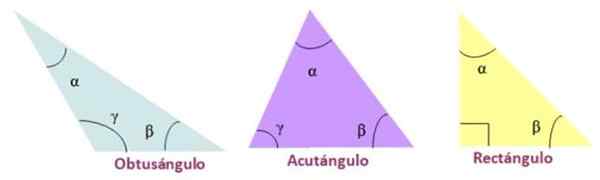Vrste trikotnika glede na svoje notranje kote. Vir: f. Zapata

Pomembni segmenti trikotnika

Med pomembnimi segmenti katerega koli trikotnika imajo:

  • Mediana, segment, usmerjen iz vrha, neposredno na nasprotno stran.
  • Mediatrix, Gre.
  • Bisektor, segment, ki deli notranji kot na dva enaka dela, in sega do nasprotne strani do kota.
  • Višina, segment pravokoten na stran, ki sega do nasprotnega vrha.
Vam lahko služi: interpolacija LaGrange

Tri srednje, tri mediatrice je mogoče zaslediti in tako naprej.

Trikotni centri

V katerem koli trikotniku izstopajo naslednje točke (glej naslednjo sliko):

  • Baricentro g, včasih tudi poklicani Centroid trikotnika je točka presečišča medianov in je vedno v notranjosti trikotnika.
  • Ortocenter h, točka, v kateri se sekajo tri višine.
  • OCCENTRO oz, Je točka presečišča mediatrics. Najdemo ga zunaj trikotnika, če je to nejas.
  • Spodbuda, presečišče za trikotnike.
  • Euler naravnost, naravnost, ki združuje baricenter, ortocenter in cenovnico, v katerem koli trikotniku, ki ni enakostraničen. Vedno je izpolnjeno, da je dolžina segmenta HG dvakrat večja od segmenta GO.
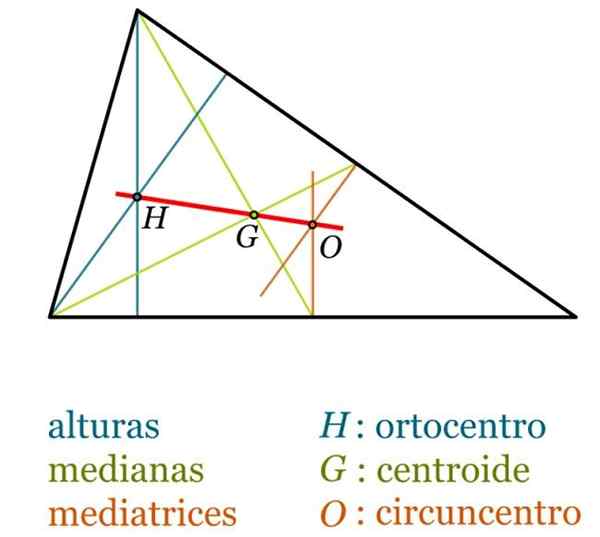Pomembne točke in segmenti trikotnika. Vir: Wikimedia Commons

Območje trikotnika

Za izračun območja A trikotnika se uporablja naslednja formula splošne narave:

A = osnova × višina / 2

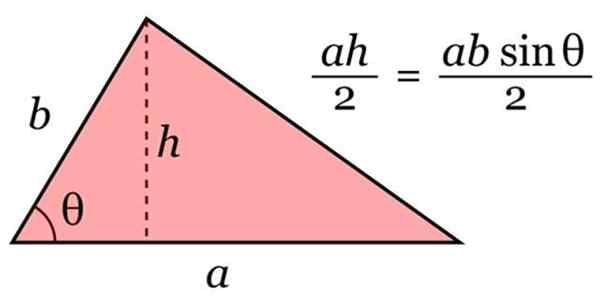Območje trikotnika. Vir: Wikimedia Commons

Herónova formula

Poznavanje dolžine vseh strani trikotnika, naslednja formula, znana kot Herónova formula, Vam omogoča iskanje območja A:

Tu so stranice trikotnika A, B in C, medtem ko je Sstr Je on polperimeter, to je polovica oboda p = a + b + c.

Reference

  1. Aleksander, d. 2013. Geometrija. 5. Izdaja. Cengage učenje.
  2. Koti. Matematika librettexts. Okrevano od: matematika.Librettexts.org.
  3. Jiménez, René. 2010. Matematika II (geometrija in trigonometrija). 2. mesto. Izdaja. Pearson.
  4. Formule vesolja. Trikotnik. Okrevano od: univerzeformulas.com.
  5. Zapata, f. Trikotniki: Zgodovina, elementi, klasifikacija, lastnosti. Pridobljeno iz: Lifer.com.