Dodatni koti, ki so, izračun, primeri, vaje

Dva ali več sta dodatni koti Če vsota njegovih ukrepov ustreza merilu ravnega kota. Ukrep ravnega kota, imenovanega tudi ploski kot, v stopinjah je 180 ° in v radianesu je π.

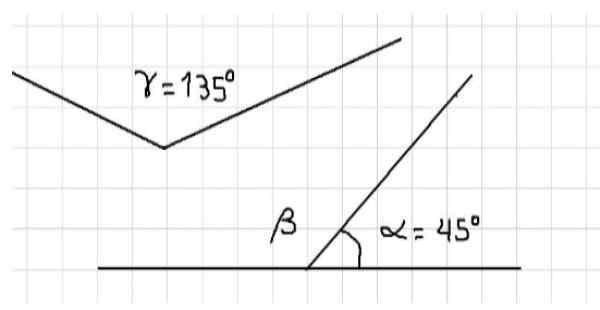
Na primer, ugotavljamo, da so trije notranji koti trikotnika dopolnili, saj je vsota njegovih ukrepov 180 °. Trije koti so prikazani na sliki 1. Iz zgoraj navedenega izhaja, da sta α in β dopolnita, saj sta sosednja in njihova polna vsota raven kot.

Slika 1: α in β sta dopolnita. α in γ sta dopolnita. Vir: f. Zapata.

Tudi na isti sliki obstajajo koti α in γ, ki sta tudi dopolnjena, ker je vsota njihovih ukrepov enaka obsegu ravnega kota, torej 180 °. Ne moremo reči, da sta kota β in γ dopolnilna, ker sta oba obtase kota, ki sta njihovi ukrepi večji od 90 °, zato njegova vsota presega 180 °.

Vir: Lafer.com

Po drugi strani lahko rečemo, da je merilo kota β enaka meri kota γ, saj je, če je β dopolnil α in γ, dopolnil α, potem β = γ = 135 °.

[TOC]

Primeri

V naslednjih primerih je treba najti neznane kote, navedene z zasliševanjem na sliki 2. Segajo od najpreprostejših primerov do nekoliko bolj izpopolnjene, kot bi moral biti bralec bolj previden.

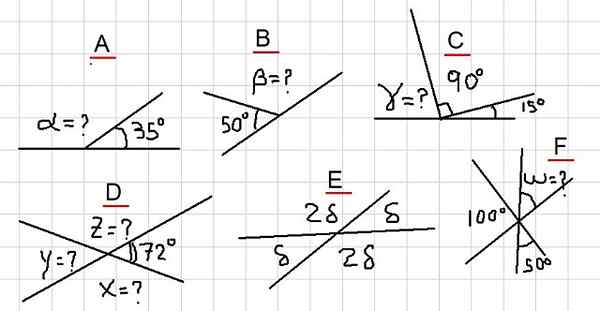Slika 2. Različni primeri dodatnih kotov. Vir: f. Zapata.

Primer a

Na sliki imamo, da sosednji koti α in 35 ° dodajata raven kot. To pomeni, da je α + 35 ° = 180 ° in zato je izpolnjeno: α = 180 °- 35 ° = 145 °.

Primer b

Ker je β dopolnil s kotom 50 °, potem sledimo, da je β = 180 ° - 50 ° = 130 °.

Vam lahko služi: kakšni so elementi prispodobe? (Deli)

Primer c

Na sliki 2C opazimo naslednjo vsoto: γ + 90 ° + 15 ° = 180 °. To pomeni, da je γ dodaten s kotom 105 ° = 90 ° + 15 °. Takrat je sklenjeno, da: 

γ = 180 °- 105 ° = 75 °

Primer d

Ker je x dopolnil z 72 °, sledi, da je x = 180 ° - 72 ° = 108 °. Poleg tega je dodatna z x, potem y = 180 ° - 108 ° = 72 °.

In končno je z dodaten z 72 °, torej z = 180 ° - 72 ° = 108 °.

Primer e

Kota Δ in 2δ sta dodatna, torej Δ + 2Δ = 180 °. Kar pomeni, da 3Δ = 180 ° in to omogoča pisanje: Δ = 180 ° / 3 = 60 °.

Primer f

Če pokličemo kot med 100 ° in 50 °, je treba do njih dopolniti.

Sledi, da u = 150 °. Ker U nasprotuje točki W, potem w = u = 150 °.

Vaje

Spodaj so predlagane tri vaje, pri vseh pa je treba vrednost kotov A in B najti v stopinjah, tako da so razmerja, prikazana na sliki 3, izpolnjena. Koncept dodatnih kotov se uporablja pri ločljivosti vseh.

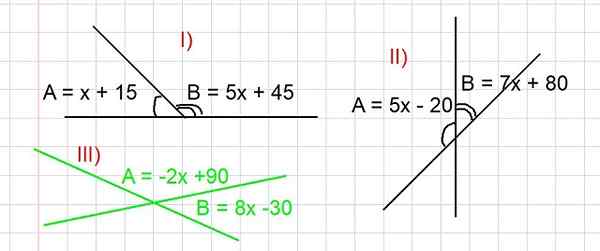Slika 3. Slika za reševanje vaj I, II in III pod dodatnimi koti. Vsi koti so izraženi v stopinjah. Vir: f. Zapata.

- Vaja I

Določite vrednosti kotov A in B dela I) slike 3.

Rešitev

A in B sta dodatna, kjer je treba nadomestiti A + B = 180 stopinj, nato pa se izraz A in B nadomestimo kot funkcija X, kot se pojavlja na sliki:

(x + 15) + (5x + 45) = 180

Dobimo linearno enačbo prve naročila. Za reševanje se izrazi vržejo: izrazi:

6 x + 60 = 180

Vam lahko služi: resnične številke: zgodovina, primeri, lastnosti, operacije

Delitev obeh članov med 6 sta::

x + 10 = 30

In končno čiščenje, sledi, da je x vreden 20 °.

Zdaj je treba vrednost x zamenjati, da najdete urejene kote. Od tam morate kotno a: a = 20 +15 = 35 °.

In s svojega dela je kot B B = 5*20 + 45 = 145 °.

- Vaja II

Poiščite vrednosti kotov A in B dela II) slike 3.

Rešitev

Kot a in b sta dopolnilni koti, a + b = 180 stopinj. Zamenjava izraza A in B kot funkcije X, ki je navedena v delu II) slike 3 je:

(-2x + 90) + (8x - 30) = 180

Spet se dobi enačba prve stopnje, za katero morajo biti izrazi priročno skupinsko:

6 x + 60 = 180

Delitev obeh članov med 6 sta::

x + 10 = 30

Kjer sledi, da je x vreden 20 °.

To pomeni, da je kot A = -2*20 + 90 = 50 °. Medtem ko kota B = 8*20-30 = 130.

- Vaja III

Določite vrednosti kotov A in B dela III) slike 3 (v zeleni barvi).

Rešitev

Kot a in b sta dopolnilni koti, a + b = 180 stopinj. Izraz A in B je treba nadomestiti kot funkcijo X, ki je navedena na sliki 3, ki jo imate:

(5x - 20) + (7x + 80) = 180

12 x + 60 = 180

Obe člani delimo za 12, da očistite vrednost x, imate:

x + 5 = 15

Končno je ugotovljeno, da je x vreden 10 stopinj.

Zdaj nadaljujte z zamenjavo, da najdete kot A: A = 5*10 -20 = 30 °. In za kota B: B = 7*10 + 80 = 150 °

Vam lahko služi: kakšen je obseg statistike? (S primeri)

Dopolnilni koti v dveh vzporednicah, ki jih razreže secat

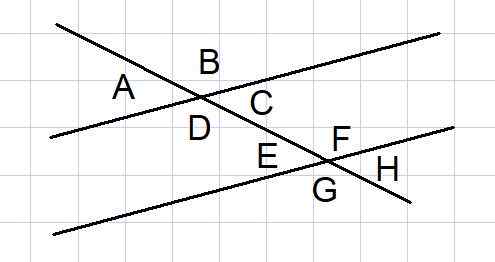Slika 4. Koti med dvema vzporednicama, ki sta jih razrezala secat. Vir: f. Zapata.

Dve vzporedni črti, ki jih sekat razrežeta, je običajna geometrijska konstrukcija v nekaterih težavah. Med takimi črtami se tvori 8 kotov, kot je prikazano na sliki 4.

Od teh 8 kotov so nekateri pari kotov dopolnili, ki jih navajamo spodaj:

1. Zunanji koti do in B, zunanjost G in H
2. Notranje kote d in c ter notranjost e in f
3. Zunanji koti A in G ter zunanji B in H
4. Notranje kote D in E ter zapornika C in F

Popolnost se imenujejo tudi enaki koti:

1. Notranje izmeničnosti: d = f in c = e
2. Zunanje izmeničnosti: a = h in b = g
3. Ustrezni: a = e in c = h
4. Nasprotja z Vertex A = C in E = H
5. Ustrezni: b = f in d = g
6. Nasprotja z vrhovnim b = d in f = g

- Vaja IV

V zvezi s sliko 4, v kateri se koti prikazujejo med dvema vzporednima črtama, ki jih razrežeta sekat, določite vrednost vseh kotov v radianih, vedoč, da je kot A = π/6 radianov.

Rešitev

A in B sta dodatna zunanja kota torej b = π - a = π - π/6 = 5π/6

A = e = c = h = π/6

B = f = d = g = 5π/6

Reference

1. Baldor, j. Do. 1973.Ravna in vesoljska geometrija. Srednjeameriška kulturna. 
2. Matematični zakoni in formule. Sistemi za merjenje kotov. Pridobljeno od: Ingemecanica.com.
3. Wentworth, g. Geometrija planeta. Okreval od: Gutenberg.org.
4. Wikipedija. Dodatni koti. Okrevano od: je.Wikipedija.com
5. Wikipedija. Transporter. Okrevano od: je.Wikipedija.com
6. Zapata f. Goniometer: Zgodovina, deli, delovanje. Pridobljeno iz: Lifer.com