Nasproti kotov z vrhom (z rešeno vajo)

The Nasproti kotov z vrhom So tisti, ki izpolnjujejo naslednje: strani ene od njih so podaljšanje strani drugega kota. On Temeljni teorem Od nasprotnih kotov z vrhom pravi: Dva kota, ki mu nasprotujeta nasprotujeta, imata enak ukrep.

Velikokrat je jezik zlorabljen z besedami, da so koti, ki jih nasprotuje vrhovi, enaki, kar ni pravilno. Dejstvo, da imata dva kota enak ukrep, še ne pomeni, da sta enaki. Kot bi rekli, da sta dva otroka, ki imata enako višino.

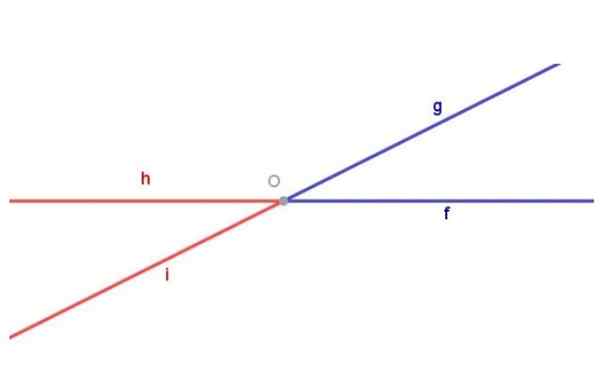
Slika 1. Nasproti kotov z vrhom. Pripravil: Fanny Zapata.

Spomnimo se, da je kot opredeljen kot geometrijska figura, sestavljena iz dveh pol -utripov z istim izvorom.

Slika 1 prikazuje kot Megla (Modra), sestavljeno iz polrearevalne [Od) in pol -utrip [OG) skupnega izvora Tudi. Slika 1 prikazuje tudi kot Hoi (rdeča), sestavljena iz polrearevalne [Slišal sem) in pol -utrip [OH) oba z izvorom Tudi. 

Dva nasprotna kota z vrhom sta dve različni geometrijski figuri. Če želite to poudariti, je na sliki 1 obarvan kot Megla Modra, medtem ko Hoi Obarval je rdečo. 

Modri ​​in rdeči koti slike 1 nasprotuje točki, ker: polčas [Od) modrega kota je podaljšanje polčasnega [OH) rdečega kota in polčasnega [OG) modrega kota je podaljšanje polčasnega [Slišal sem) rdečega kota.

[TOC]

Pomembni koncepti o kotih

Strani in točke kota

Geometrijska figura, sestavljena iz dveh pol -utripov s skupnim izvorom, je kot. Naslednja slika prikazuje kot Poq tvorita dva polčasnega [OP) in [OQ) skupnega izvora Eno:

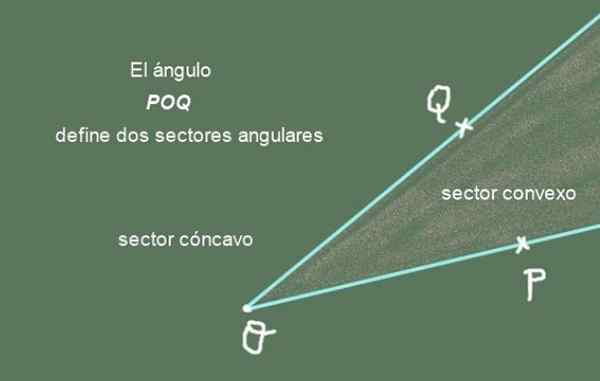Slika 2. Kot POQ določa dva kotna sektorja. Pripravil: F. Zapata.

Pol -utrip [OP) in [OQ) so strani kota Poq, Medtem ko je skupna točka ali se imenuje Vértice kota.

Vam lahko služi: Sturges pravilo

Kotni sektor: Kot deli ravnino, ki ga vsebuje v dva kotna sektor. Eden od njih je konveksni kotni sektor, drugi pa konkavni kotni sektor. Zveza obeh sektorjev daje popolno letalo.

Slika 2 prikazuje pod kotom Poq in njegova dva kotna sektor. Konveksni kotni sektor je tisti, ki ima koničasto obliko, konkavni pa kotni sektor ravnine, ki manjka konveksnega sektorja.

Koti, ki jih tvorita dve vrstici, ki sta razrezani

Dve vrstici ravnine, ki sta prestrežena, tvorita štiri kote in ravnino razdelita na štiri kotne sektorje.

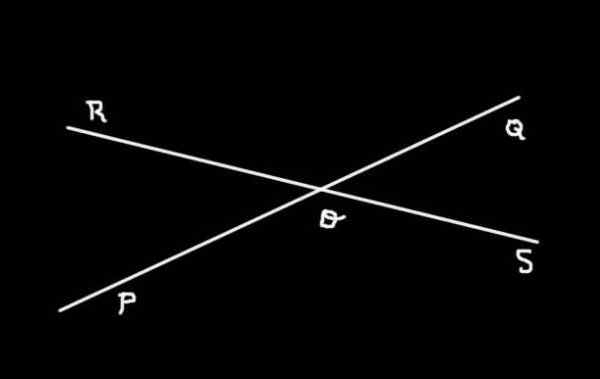Slika 3. Vrstice (PQ) in (Rs) so prestrežene v kotih O in obrazca 4. Pripravil: F. Zapata.

Slika 3 prikazuje dve vrstici (PQ) in (Rs) prestreženo Tudi. Tam lahko vidite, da so določeni štirje koti:

-Soq, Qor, Rop in Pos

Koti Soq in Qor, Qor in Rop, Rop in Pos, Pos in Soq so  sosednji koti med seboj, medtem ko Soq in Rop Nasprotujejo jim vrhovi. Tudi oni Nasproti kotov z vrhom Koti Qor in Pos.

Pravokotne črte in ravni kot

Dve sušilni črti (ravne črte sekajo) sta Pravokotne ravne črte Če določijo štiri kotne sektorje enakega merila. Če je vsak od štirih sektorjev simetričen s sosednjim kotnim sektorjem, potem ima enak ukrep.

Vsak od kotov, ki določata obe pravokotni črti, se imenuje pravi kot. Vsi ravni koti imajo enak ukrep.

Pol -utrip na isti črti in ravnem kotu

Glede na črto in točko, sta definirana dva polčas. Ta dva pol -ustra definirata dva Ravni koti.

Na sliki 3 je mogoče opaziti črto (Rs) in točka Tudi ki pripada (Rs). Kot Sor Je raven kot. Prav tako je mogoče potrditi, da je kot Ros Je raven kot. Vsi ravni koti imajo enak ukrep.

Vam lahko služi: klasurativna lastnina

Ničelni kot in polni kot

En sam pol -rearetional določa dva kota: eden od njih v konveksnem kotnem sektorju je ničelni kot In drugi, konkavni kotni sektor je Popoln kot. Na sliki 3 ničelni kot Sos in Popoln kot Sos. 

Meritev 

Obstajata dva numerična sistema, ki se pogosto uporabljata za merjenje kota. 

Eden od njih je sistem SexageSimal, torej na podlagi številke 60. Gre za dediščino starodavnih mezopotamskih kultur. Drugi merilni sistem kotov je sistem Radián, ki temelji na številu π (PI) in je zapuščina starogrških modrecev, ki so razvili geometrijo.

SexagesImalni sistem

Ničelni kot: V sistemu SexageSimal NULL kot meri 0 ° (nič stopinj).

Popoln kot: Ukrep 360 ° je dodeljen (tristo šestdeset stopinj).

Ravni kot: V sistemu SexageSimal Ravni kot meri 180 ° (sto osemdeset stopinj).

Pravi kot: Dve pravokotni črti razdelita ravnino na štiri kote enakega merila, imenovane ravne kote. Ukrep desnega kota je četrtina celotnega kota, to je 90 ° (devetdeset stopinj).

Transporter ali goniometer

Transporter je instrument, ki se uporablja za merjenje kotov. Sestavljen je iz polkroga (običajno prozorne plastike), razdeljen na 180 kotnih odsekov. Ker polkrog tvori raven kot, je ukrep med dvema zaporednima odsekoma 1.

Goniometer je podoben transporterju in je sestavljen iz kroga, razdeljenega na 360 kotnih odsekov.

Kot, katerega stranice se začnejo od središča goniometra, prestrežejo dva sektorja in merilo tega kota v stopinjah je enak številu N odsekov med obema prestreljenimi sektorji, v tem primeru bo ukrep štEne stopinje”).

Lahko vam služi: kvadratni centimetri do kvadratnih metrov (cm² do m²)

Izrek nasprotnih kotov z vrhom

Formalno je na ta način naveden teorem:

Če dva kota nasprotujeta točki, potem imata enak ukrep.

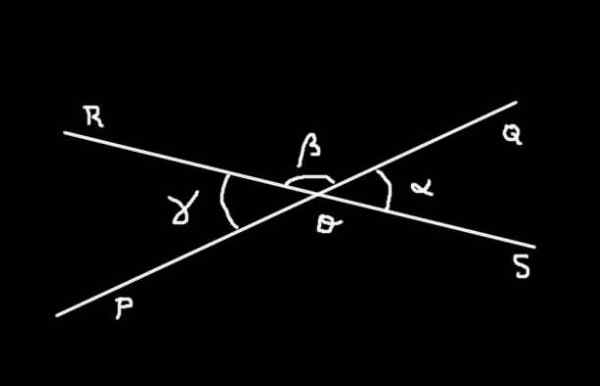Slika 4. α, β in γ so ukrepi kotov SOQ, QOR in ROP. Pripravil: F. Zapata.

Demonstracija

Kot Soq Ima α merilo; kot Qor Ima β merilo in kot Rop Ima γ merilo. Vsota kota Soq več njega Qor tvori ploščat kot Sor ukrepa 180 °.

To je:

α + β = 180 °

Na drugi strani in uporaba istega sklepanja z koti Qor in Rop Imaš:

β + γ = 180 °

Če opazimo dve prejšnji enačbi, je edini način, da sta oba izpolnjena, ta, da je α enak γ.

Kot Soq Ima α ukrep in nasprotuje vrhovi Rop ukrepa γ in kot α = γ sklepamo, da imajo koti, ki jim nasprotujejo vrhovi.

Vaja rešena

V zvezi s sliko 4: predpostavimo, da je β = 2 α. Poiščite mero kotov Soq, Qor in Rop Pri seksualnih stopnjah.

Rešitev

Kot vsota kota Soq več njega Qor tvori ploščat kot Sor Imaš:

α + β = 180 °

Vendar nam povedo, da je β = 2 α. Če zamenjamo to vrednost β, ostanemo:

α + 2 α = 180 °

To pomeni:

3 α = 180 °

Kar pomeni, da je α tretji del 180 °:

α = (180 ° / 3) = 60 °

Nato merilo Soq je α = 60 °. Merilo Qor je β = 2 α = 2*60º = 120 °. Končno kot Rop nasprotuje vrhovi Soq potem je glede na teorem dokazal, da imajo enak ukrep. To je merilo Rop je γ = α = 60 °. 

Reference

1. Baldor, j. Do. 1973.Ravna in vesoljska geometrija. Srednjeameriška kulturna. 
2. Matematični zakoni in formule. Sistemi za merjenje kotov. Pridobljeno od: Ingemecanica.com.
3. Wikipedija. Nasproti kotov z vrhom. Okrevano od: je.Wikipedija.com
4. Wikipedija. Transporter. Okrevano od: je.Wikipedija.com
5. Zapata f. Goniometer: Zgodovina, deli, delovanje. Pridobljeno iz: Lifer.com