Naključna metodologija vzorčenja, prednosti, slabosti, primeri

On naključno vzorčenje To je način, kako iz izbire statistično reprezentativnega vzorca iz določene populacije. Del načela, da mora imeti vsak element vzorca enako verjetnost, da bo izbran.

Žrebanje je primer naključnega vzorčenja, v katerem je dodeljen vsakemu članu prebivalstva udeležencev. Izbrati številke, ki ustrezajo nagradnim nagradam (vzorcem), se uporablja nekaj naključne tehnike, na primer izvleček iz nabiralnika številk, ki so bile ocenjene na enakih karticah.

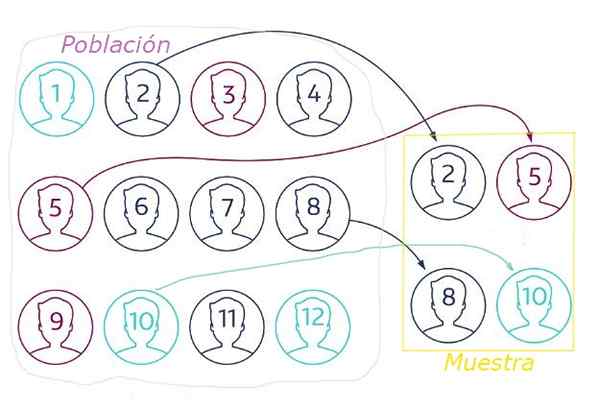Slika 1. V naključnem vzorčenju se vzorec pridobiva iz naključne populacije z neko tehniko, ki zagotavlja, da imajo vsi elementi enako verjetnost, da bodo izbrani. Vir: NetQuest.com.

Pri naključnem vzorčenju je bistvenega pomena.

[TOC]

Velikost vzorca

Obstajajo formule za določitev ustrezne velikosti vzorca. Najpomembnejši dejavnik, ki ga je treba upoštevati, je, ali je znana velikost prebivalstva. Oglejmo si formule, da določimo velikost vzorca:

Primer 1: Velikost prebivalstva ni znana

Ko velikost prebivalstva ni znana, je mogoče izbrati ustrezen n vzorca, da ugotovite, ali je določena hipoteza resnična ali napačna.

Za to se uporablja naslednja formula:

n = (z² P q)/(e²)

Kje:

-P je verjetnost, da je hipoteza resnična.

-Q je verjetnost, da ni, torej q = 1 - p.

-E je relativna meja napake, na primer 5 -odstotna napaka ima marža E = 0,05. 

-Z je povezan s stopnjo zaupanja, ki jo zahteva študija.

Vam lahko služi: normalna porazdelitev: formula, značilnosti, primer, vadba

V normalni porazdelitvi (ali normalizirani) ima 90 -odstotna stopnja zaupanja z = 1.645, ker je verjetnost, da je rezultat med -1,645σ in +1,645σ 90%, kjer je σ standardni odklon.

Ravni zaupanja in ustrezne vrednosti z 

1.- 50 -odstotna stopnja zaupanja ustreza z = 0,675.

2.- 68.3% stopnja zaupanja ustreza z = 1.

3.- 90 -odstotna raven zaupanja, enakovredna z = 1.645.

4.- 95 -odstotna stopnja zaupanja ustreza z = 1,96

5.- 95,5% stopnja zaupanja ustreza z = 2.

6.- 99,7% stopnja zaupanja je enakovredna z = 3.

Primer, v katerem je mogoče uporabiti to formulo, bi bil v raziskavi za določitev povprečne teže kamenčkov plaže.

Očitno ni mogoče študirati in tehtati vseh kamenčkov plaže, zato je priročno.

Slika 2. Za preučevanje značilnosti kamenčkov plaže je treba izbrati naključni vzorec z reprezentativnim številom. (Vir: Pixabay)

Primer 2: Velikost prebivalstva je znana

Ko je znano število n elementov, ki sestavljajo določeno populacijo (ali vesolje), če želite izbrati s preprostim naključnim vzorčenjem statistično pomembnega vzorčnega vzorca, je to formula: 

n = (z²p q n)/(n e² + Z²P Q)

Kje:

-Z je koeficient, povezan s stopnjo zaupanja.

-P je verjetnost uspeha hipoteze.

-Q je verjetnost odpovedi v hipotezi, p + q = 1.

-N je velikost celotne populacije.

-E je relativna napaka rezultata študije.

Primeri

Metodologija za pridobivanje vzorcev je veliko odvisna od vrste študije, ki je potrebna. Zato ima naključno vzorčenje nešteto aplikacij:

Vam lahko služi: znaki združevanja

Ankete in vprašalnike

Na primer v telefonskih anketah se ljudje odločijo za posvetovanje s pomočjo generatorja naključnih številk, ki velja za regijo v študiji.

Če želite za zaposlene v velikem podjetju uporabiti vprašalnik, se lahko izbor anketirancev uporablja prek številke zaposlene ali številke osebne izkaznice.

To številko je treba izbrati tudi naključno z uporabo generatorja naključnih številk.

Slika 3. Vprašalnik je mogoče uporabiti naključno izbiro udeležencev. Vir: Pixabay.

QA

V primeru, da je študija na delih, ki jih izdeluje stroj, mora biti dele izbran naključno, vendar za sklope, narejene v različnih obdobjih dneva ali v različnih dneh ali tednih.

Prednosti

Preprosto naključno vzorčenje:

- Omogoča zmanjšanje stroškov statistične študije, saj ni treba preučiti celotne populacije, da bi dosegli statistično zanesljive rezultate, z želeno stopnjo zaupanja in stopnjo napak, potrebne v študiji.

- Izogibajte se pristranskosti: Ker je izbira elementov, ki jih je treba preučiti, popolnoma naključna, študija zvesto odraža značilnosti populacije, čeprav je bil le del istega preučeno.

Slabosti

- Metoda ni ustrezna v primerih, ki jih želite vedeti v različnih skupinah ali slojih populacije.

V tem primeru je zaželeno predhodno določiti skupine ali segmente, na katerih je študija opravljena. Ko so sloji ali skupine definirani, potem, če je primerno, da vsak od njih uporabi naključno vzorčenje.

- Zelo malo verjetno je, da se pridobijo informacije o manjšinskih sektorjih, od katerih je včasih treba vedeti njihove značilnosti.

Lahko vam služi: pravilo Simpsona: formula, demonstracije, primeri, vaje

Na primer, če gre za kampanjo dragega izdelka, je treba vedeti preference najbogatejših manjšinskih sektorjev.

Vaja rešena

Želimo preučiti preferenco populacije tako, kot je Cola of Cola, vendar v tej populaciji ni predhodne študije, o kateri njena velikost ni znana.

Po drugi strani mora biti vzorec reprezentativen z najnižjo stopnjo zaupanja 90%, sklepi pa morajo imeti odstotno napako v višini 2%.

-Kako določiti velikost S vzorca?

-Kakšna bi bila velikost vzorca, če je stopnja napake do 5%?

Rešitev

Ker velikost populacije ni znana, za določitev velikosti vzorca se uporablja zgoraj navedena formula:

n = (z²P q)/(e²)

Domnevamo, da obstaja enaka verjetnost preferenc (p) z našo osvežitvijo, ki ni bila non -norca (q), potem je p = q = 0,5.

Po drugi strani pa mora imeti rezultat študije odstotek napake manj kot 2%, potem bo relativna napaka 0,02.

Končno vrednost z = 1.645 ustvari 90 -odstotno stopnjo zaupanja.

Skratka, imate naslednje vrednosti:

Z = 1.645

P = 0,5

Q = 0,5

E = 0,02

S temi podatki se izračuna minimalna velikost vzorca:

N = (1.645² 0,5 0,5)/(0,02²) = 1691.3

To pomeni, da mora študija z merom potrebnih napak in z izbrano stopnjo samozavesti mora imeti vzorec anketirancev vsaj 1692 posameznikov, izbranih s preprostim naključnim vzorčenjem.

Če greste od stopnje napake od 2% do 5%, potem je nova velikost vzorca:

N = (1.645² 0,5 0,5)/(0,05²) = 271

Kar je bistveno manjše število posameznikov. Za zaključek je velikost vzorca zelo občutljiva na želeni rob v študiji.

Reference

1. Berenson, m. 1985.Statistika za administracijo in gospodarstvo, koncepte in aplikacije. Interameriški uvodnik.
2. Statistika. Naključno vzorčenje. Vzet iz: enciklopediaeconomica.com.
3. Statistika. Vzorčenje. Iztegnjeno od: statistike.Podstavek.USON.mx.
4. Raziskovalno. Naključno vzorčenje. Okrevano od: Raziskovalno.com.
5. Moore, d. 2005. Uporabljena osnovna statistika. 2. mesto. Izdaja.
6. Netquest. Naključno vzorčenje. Okrevano od: NetQuest.com.
7. Wikipedija. Statistično vzorčenje. Pridobljeno iz: v.Wikipedija.org