Primeri metode paralelograma, rešene vaje

On Metoda paralelograma To je grafična metoda za dodajanje dveh vektorjev v ravnino. Pogosto se uporablja za iskanje rezultata dveh sil, ki se nanašajo na telo ali dve hitrosti, kot v primeru plavalca, ki namerava pravokotno prečkati reko in ga preusmeri tok tok.

Za izgradnjo paralelograma se mora izvor vektorjev, ki jih je treba dodati, narisati v obsegu.

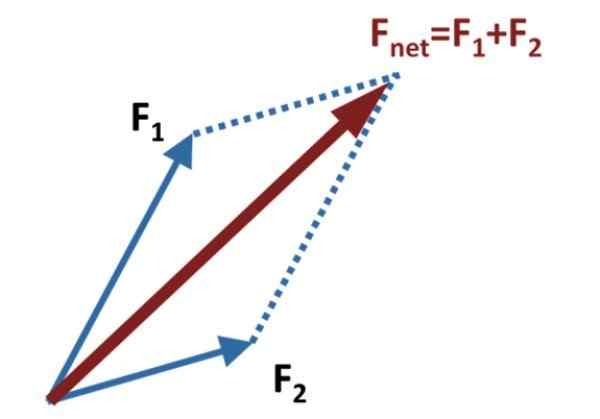
Slika 1. Metoda paralelograma za dodajanje dveh vektorjev. Vir: Wikimedia Commons.

Nato se pomožne črte potegnejo vzporedno z vsakim vektorjem, ki dosežejo konec drugega, kot je prikazano na zgornji sliki.

Dodajanje ali posledično vektor, imenovan tudi net Force, je vektor F_mreža, to dobimo z risanjem vektorja, ki sega iz skupnega izvora F₁ in F₂, do točke, ko se pomožne vzporedne črte sekajo. V diagramu slike so predstavljene s pikčastimi črtami.

Metoda prejme svoje ime na sliki, ki je nastala z odvisniki in pomožnimi črtami, kar je natančno paralelogram. Glavna diagonala paralelograma je vektor vsote.

Zelo pomembno je poudariti, da vrstni red, v katerem so nameščeni dodatni vektorji.

[TOC]

Primer metode paralelograma korak za korakom

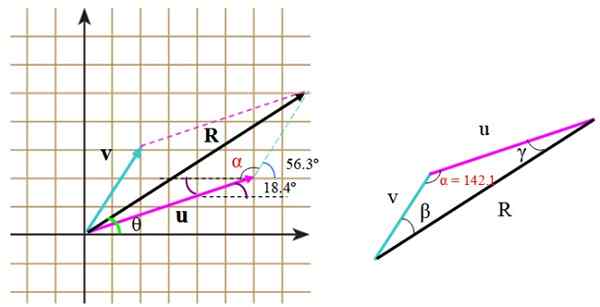
Naslednja slika prikazuje vektorje v in ali V poljubnih enotah. Vektor v Ukrepi 3.61 enot in tvori kot 56.3. z vodoravnim ali Ukrepi 6.32 enot in kot 18.4 ° glede te referenčne vrstice.

Vam lahko služi: Naključna napaka: formula in enačbe, izračun, primeri, vaje

Najdimo, da vaš vektor doda prek metode paralelograma.

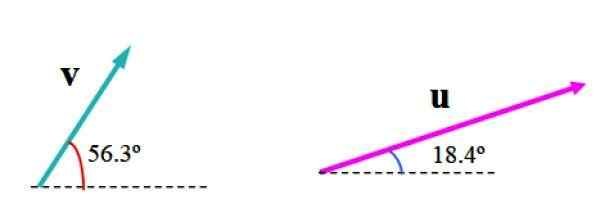Slika 2. Vsaka dva vektorja v ravnini, od katerih želimo najti dobljeni vektor. Vir: f. Zapata

Izbrati je treba ustrezno lestvico, na primer tisto, prikazano na naslednji sliki, v kateri je bila ravnina razdeljena z mrežo. Širina kvadrata predstavlja eno (1) enoto.

Ker se vektorji ne spreminjajo, ko se prenesejo, so nameščeni tako, da njihov izvor sovpada z izvorom koordinatnega sistema (slika levice).

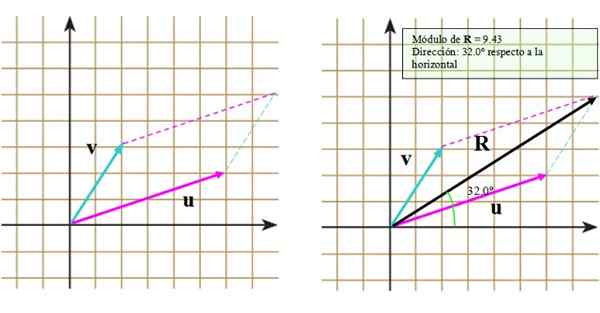Slika 3. Vsota vektorjev po metodi paralelograma. Vir: f. Zapata.

Zdaj pa sledimo tem korakom:

1. Vektor konec vektorja v Segmentirana črta, ki je vzporedna z vektorjem ali.
2. Ponovite postopek, vendar tokrat s koncem vektorja ali.
3. Narišite glavno diagonalo, ki sega od skupnega izvora do točke presečišča segmentiranih linij.

Rezultat je mogoče videti na pravi sliki, v kateri se pojavi nastali vektor R.

Če želimo vedeti velikost R, Lahko izmerimo njegovo dolžino in jo primerjamo z lestvico, ki jo imamo. In kar zadeva njihovo smer, lahko na primer uporabimo vodoravno osi ali navpično os, na primer kot reference.

Z uporabo vodoravne osi ali osi x, kot R Obrazec s to osi se meri s transporterjem in na ta način poznamo naslov R.

Tudi velikost in smer R Izračunamo jih lahko s teoremi kosinusa in dojke, saj lahko nastali paralelogram razdelimo na dva skladna trikotnika, katerih stranice so moduli vektorjev ali, v in R. Glej primer Rešen 1.

Vam lahko služi: trenutna hitrost: definicija, formula, izračun in vaje

Poseben primer: vsota pravokotnih vektorjev

Ko so vektorji pravokotni drug na drugega, je oblikovana figura pravokotnik. Nastali vektorski modul ustreza dolžini diagonale, ki jo je mogoče enostavno izračunati s teoremom Pythagoras.

Slika 4. Vsota dveh pravokotnih vektorjev z uporabo metode paralelograma. Vir: f. Zapata.

Rešene vaje

- Vaja 1

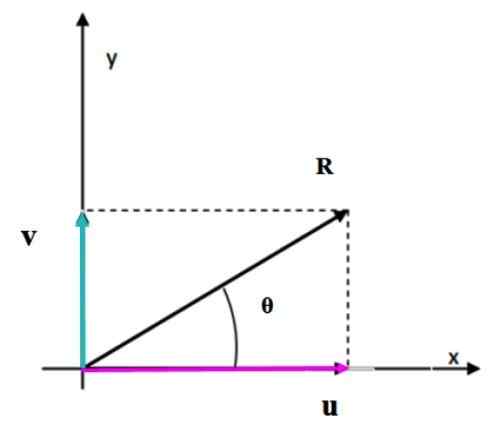
Imate vektor v, ki meri 3.61 enot in tvori kot 56.3. z vodoravnim in vektorjem ali, čigar ukrep je 6.32 enot in tvori kot 18.4. (slika 2). Določite nastali vektorski modul R = ali + v in smer, ki tvori omenjeni vektor z vodoravno osi.

Rešitev

Metoda paralelograma se uporablja v skladu z zgoraj opisanimi koraki, da dobimo vektor R. Kot je navedeno doslej, če se vektorji skrbno narišejo po lestvici in uporabljajo pravilo in transporter, velikost in smer R Se merijo neposredno na risbi.

Slika 5.- Izračun obsega in smeri nastalega vektorja. Vir: f. Zapata.

Izračunamo jih lahko tudi neposredno, s pomočjo trigonometrije in lastnosti kotov. Ko tvori trikotnik ni pravokotnik, kot v tem primeru, se za iskanje manjkajoče strani nanese teorem za kosinus.

V desnem trikotniku strani merijo U, V in R. Za nanašanje kosinusnega teorema je treba poznati kot med v in ali, da lahko najdemo s pomočjo omrežja in pravilno nameščeno kote, ki jih dobavlja izjava.

Ta kot je α in je sestavljen iz:

α = (90–56.3.) + 90 ° +18.4. = 142.1

Vam lahko služi: rdeči pritlikavec

Glede na teorem Coseno:

R² = v² + ali² - 2u⋅v⋅cos α = 3.61² + 6.32² - 23.61 × 6.32 × cos 142.1st = 88.98

R = 9.43 enot.

Končno, kot med R In vodoravna os je θ = 18.4 º + γ. Kot γ najdemo s teoremom dojk:

sin α / r = sen γ / u

Zato:

sin γ = v (sin α / r) = 3.61 x (Sen 142.1. / 9.43)

γ = 13.6

θ = 18.4 º + 13.6 ° = 32 °

- Vaja 2

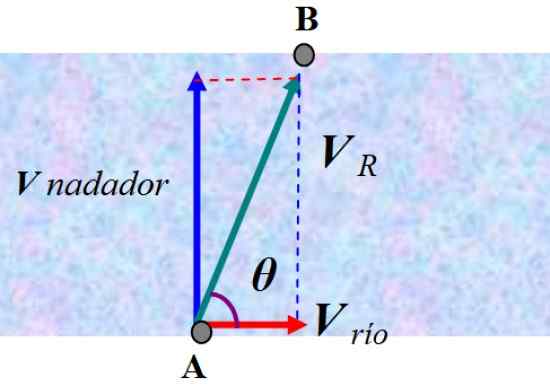
Plavalec se pripravlja na prečkanje reke, ki plava pravokotno na tok s konstantno hitrostjo 2.0 m/s. Plavalec se začne od A, vendar se konča v B, spodnja točka, zaradi toka, ki ga je preusmeril.

Če je hitrost toka 0.8 m/s in vse hitrosti naj bi našli hitrost plavalca, kot jo vidi opazovalec, ki stoji na obali.

Rešitev

Slika 6. Vsota hitrosti po metodi paralelograma. Vir: f. Zapata.

Opazovalec, ki stoji na obali, bi videl, kako se plavalec preusmeri glede na nastalo hitrost V_R. Če želite najti odgovor, moramo dodati hitrost plavalca in hitrost toka, ki jo pokličemo V _reka:

V _R = V _plavalec + V _reka

Na sliki, ki ni v obsegu, smo dodali vektorje, da smo dobili V _R. V tem primeru lahko za pridobitev njegovega obsega uporabimo teorem pitagore:

V_R² = 2.0² + 0.8² = 4.64

V_R = 2.15 m/s

Naslov, v katerem se plavalec pravokotne smeri zlahka izračuna in opazi, da:

θ = arctg (2/0.8) = 68.2. mesto

Potem plavalec odstopa 90 ° - 68.2. = 27.2. vašega prvotnega naslova.

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
2. Bedford, 2000. Do. Mehanika za inženiring: statična. Addison Wesley.
3. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika. Uredil Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fizika. 2. mesto. Ed. McGraw Hill.
5. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1.