Vsota grafične metode vektorjev, primeri, rešenih vaj

The vsota vektorjev To je dodatna operacija med vektorji, ki ima za posledico drug vektor. Za vektorje je značilno, da imajo velikost ter tudi smer in pomen. Zato jih na splošno ni mogoče dodati, kot bi to storili s skalarnimi količinami, torej dodajanje številk.

Vektor, pridobljen iz vsote več vektorjev, se imenuje posledično vektor. V mehaniki govorimo o posledična sila, ki je vektorska vsota vseh sil na telesu. Ta rezultat je enak naboru ali sistemu sil.

Če želite v celoti določiti vektor vsote, je treba navesti velikost in enotnost, smer in pomen.

Pomembno je poudariti, da morajo z dodajanjem vektorjev predstavljati enako fizično velikost, zato je vektorska vsota homogena operacija. To pomeni, da lahko z drugo dodamo eno silo, vendar ne s silo z premikom, saj je rezultat nesmiselno.

Na voljo je več metod za iskanje dobljenega vektorja: grafika in analitika. Če želite najti vektorske vsote z grafičnimi metodami, temelji na preprosti predstavitvi za vektor, in sicer na segmentno usmerjeno ali puščico, kot je ta:

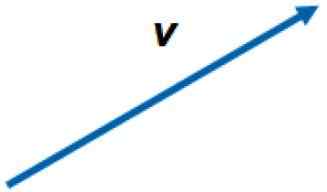Grafični prikaz vektorja v ravnini. Vir: f. Zapata.

Vektorji so označeni s črnimi črkami v tiskanem besedilu ali s puščico nad črko, da jih ločimo od njihovih velikosti ali od skalarnih količin. Na primer obseg vektorja v Preprosto je v.

[TOC]

Grafična metoda za dodajanje vektorjev

Za dodajanje več kot dveh vektorjev, Metoda poligona tudi poligon, ki sestavljajo prenos na vsakega od naslovljenih vektorjev. Značilnost vektorjev je, da so invariantni glede prevoda, zato bomo to lastnost uporabili za vzpostavitev vsote.

Vam lahko služi: toplotna dilatacija

Začne se s katerim koli od vektorjev, saj je dodajanje vektorja komutativen in vrstni red dodatkov ne spremeni vsote. Drugi vektor se premakne spodaj in ustreza svojemu izvoru s koncem prvega.

Nato ga pripeljemo do naslednjega vektorja in nato damo isti postopek, ki naj bi se ujemal s poreklom s koncem prejšnjega. Nadaljujemo na ta način, da postavimo zadnji vektor.

Nastali vektor je tisti, ki se pridruži izvoru prvega s prostim koncem zadnjega. Ime te metode izvira iz slike, ki ima za posledico: poligon.

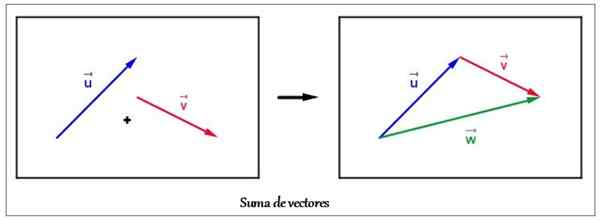
Primer

Primer dveh vektorjev v ravnini z grafično metodo. Vir: Wikimedia Commons

Vzemimo kot primer vsota dveh vektorjev ali in v ki je prikazan na zgornji sliki.

Začenši z vektorjem ali, Preselil se je v vektor v Da se svoj izvor ujema s koncem prvega. Nastali vektor W Izvišeno je iz izvora ali do konca v, tvori tristransko figuro: trikotnik. Zato se v tem posebnem primeru imenuje postopek Metoda trikotnika.

Upoštevajte, da je pomembna podrobnost, velikost ali modul nastalega vektorja ni vsota modulov dodatnih vektorjev. Pravzaprav je skoraj vedno manj, razen če so vektorji vzporedni.

Poglejmo spodaj, kaj se zgodi v tem primeru.

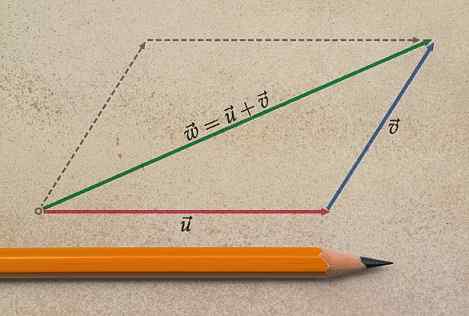
Poseben primer: vsota vzporednih vektorjev

Opisano metodo je mogoče uporabiti tudi za poseben primer, v katerem so vektorji vzporedni. Razmislite o naslednjem primeru:

Vam lahko služi: Boltzmann Constant: Zgodovina, enačbe, izračun, vajeVsota vzporednih vektorjev. Vir: f. Zapata.

Vektor je ostal v V prvotnem položaju in se premakne v vektor ali na tak način, da se njen izvor strinja s koncem  v. Zdaj je iz izvora iz izvora v In konec ali.

To je dobljeni vektor W in njegova velikost je vsota velikosti oglasov. Smer in smer treh vektorjev je enaka.

Nastali vektor ima največji modul, če dodatki tvorijo kot 0 °, na primer tisti primera. Če vektorji med seboj tvorijo kot 180 °, potem ima dobljeni vektor minimalni modul.

Primeri vsote vektorjev

- Premiki

Kolesar potuje najprej 3 km proti severu in nato 4 km zahodno. Vaš premik, ki ga imenujemo R, Z lahkoto ga najdemo z metodo trikotnika in referenčnim sistemom, kjer so kardinalne točke označene:

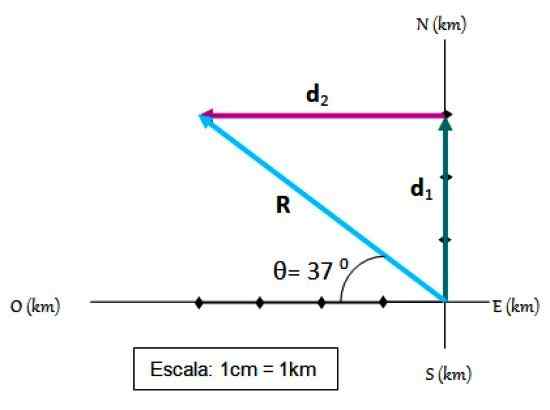Ki je posledica dveh premikov. Vir: f. Zapata.

Koraki za dodajanje vektorja

-Izhodišče sovpada z izvorom referenčnega sistema.

-Na koordinatnih osi je izbrana lestvica, ki je v tem primeru 1 cm = 1 km

-Prvi premik je narisan na lestvici d_1.

-Potem a d₁ Drugi premik je narisan d₂, Tudi v obsegu.

-Posledično premik R Je vektor, ki sega od izvora do konca d₂.

-Velikost R Meri se s postopnim pravilom, enostavno je preveriti, ali je r = 5.

-Končno kot, ki R Obrazec z vodoravno se meri s pomočjo transporterja in se izkaže za θ = 37 ⁰

- Posledična hitrost

Plavalec želi prečkati reko in za to nič s hitrostjo 6 km/h, pravokotno na obalo, vendar tok, ki nosi hitrost 4 km/h, odstopa.

Lahko vam služi: ohm: Odpornost, primeri in rešeni vaja

Če želite vedeti, da je nastala hitrost, se dodajo vektorji plavalcev, ki so bili narisani navpični in tok, kar je vodoravno.

Po grafični metodi dobimo nastalo hitrost v_R:

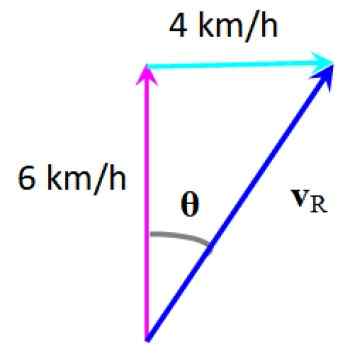Posledična hitrost. Vir: f. Zapata.

Odstopanje, ki ga doživlja plavalec, lahko izračunamo z:

θ = arctg (4/6) = 33.7. desno od začetnega naslova

Obseg njegove hitrosti se poveča, ker hitrost reke dodaja vektorsko. Lestvico lahko najdete previdno, kot v prejšnjem primeru.

Ali s pomočjo trigonometričnih razlogov 33.7. mesto:

Sen 33.7. = 4/v_R

v_R = 4/ greh 33.7. = 7.21 km/h

Vaja rešena

Na delcu delujejo naslednje sile, katerih velikosti so navedene spodaj:

F₁= 2.5 n; F₂= 3 n; F₃= 4 n; F₄= 2.5 n

Poiščite nastalo silo.

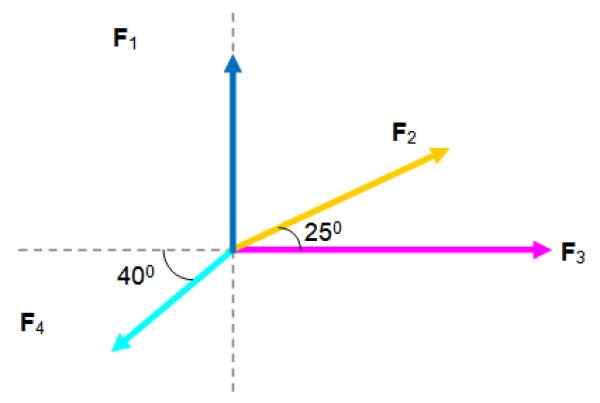Sistem koplanarnih sil. Vir: f. Zapata.

Rešitev

Lahko dodamo grafično začenši s katerim koli vektorjem, saj je vektorska vsota komutativna.

Na sliki A se je začel z F₁. Vzpostavitev lestvice in s pomočjo pravila in oddelkov se drugi vektorji prenesejo, da jih postavijo drug za drugim.

Vektor F_R je usmerjen iz izvora F₁ do konca F₄. Njegova velikost je 5.2 n in tvori kot 26.5. glede na vodoravno.

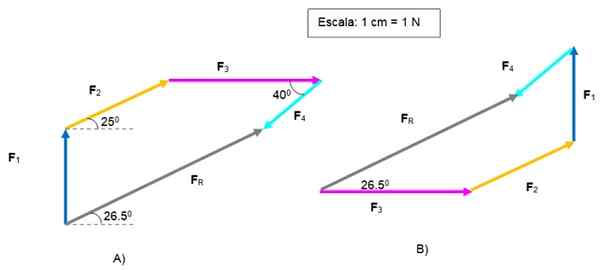Vektorska grafična vsota. Vir: f. Zapata.

Na sliki B je bil rešen isti problem, začenši z F₃ in konča z F₄, Da bi dobili isto F_R .

Poligoni so različni, vendar je rezultat enak. Bralec lahko ponovno preizkusi vrstni red vektorjev.

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
2. Bedford, 2000. Do. Mehanika za inženiring: statična. Addison Wesley.
3. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika. Uredil Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fizika. 2. mesto. Ed. McGraw Hill.
5. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1.