Značilnosti minimalnih stroškov, prednosti, slabosti

On Metoda minimalnih stroškov Gre za postopek, ki se uporablja za pridobitev začetne izvedljive rešitve za prevoz. Uporablja se, kadar je prednostna naloga zmanjšanje stroškov distribucije izdelkov.

Metoda minimalnih stroškov želi doseči najnižje stroške prevoza med več centri povpraševanja (destinacije) in več oskrbovalnih centrov (viri).

Vir: Pixabay.com

Proizvodna zmogljivost ali dobava vsakega vira ter zahteva ali zahteva vsakega cilja so znana in fiksna.

Stroški prevoza enote izdelka so znani tudi od vsakega vira do vsakega cilja.

Izdelek je treba prepeljati iz več virov na različne destinacije tako, da zadosti povpraševanju vsakega cilja in hkrati zmanjšati skupne stroške prevoza.

Druge metode je mogoče uporabiti, če je prioriteta prihranek časa, namesto da bi prihranili stroške.

[TOC]

Značilnosti

Optimalna razporeditev izdelka iz različnih virov na različne destinacije se imenuje Problem prometa.

- Prevozni modeli se ukvarjajo z izdelkom, izdelanim v različnih rastlinah ali tovarnah (viri dobave) v več skladiščih (destinacije povpraševanja).

- Cilj je izpolniti zahteve destinacij v okviru omejitev proizvodne zmogljivosti rastlin, na minimalne stroške prevoza.

Koraki metode minimalnih stroškov

Korak 1

Izbrana je celica, ki vsebuje najnižje stroške transporta celotne tabele. Ta celica je dodeljena čim več enot. Ta znesek je mogoče omejiti z omejitvami ponudb in zahtev.

V primeru, da ima več celic najnižje stroške, bo celica izbrana tam, kjer je mogoče doseči največjo dodelitev.

Vam lahko služi: analitični postopek (računovodstvo)

Nato nadaljujemo s prilagajanjem ponudbe in povpraševanja, ki je v vrstici in stolpcu. Prilagodimo ga tako, da odštejemo količino, dodeljeno celici.

2. korak

Vrstica ali stolpec, v kateri je (bodisi nič) izčrpana, dobava ali povpraševanje se odpravi.

V primeru, da obe vrednosti, ponudba in povpraševanje, bodisi enaka nič, lahko katero koli vrstico ali stolpec odpravimo, poljubno odpravljeno.

Korak 3

Prejšnji koraki se ponovijo z naslednjimi nižjimi stroški in se nadaljujejo, dokler celotna ponudba, ki je na voljo v različnih virih, ali vso povpraševanje po različnih destinacijah.

Prijave

- Zmanjšajte stroške prevoza tovarn na skladišča ali skladišča v maloprodajnih trgovinah.

- Določite lokacijo minimalnih stroškov nove tovarne, skladišča ali prodajne pisarne.

- Določite časovni načrt proizvodnje minimalnih stroškov, ki ustreza povpraševanju podjetja z omejitvami proizvodnje.

Prednosti

Šteje se, da metoda minimalnih stroškov daje natančnejše in optimalne rezultate v primerjavi z metodo severozahodnega vogala.

To je zato, ker metoda severozahodnega vogala samo daje pomembnosti za zahtevo po ponudbi in razpoložljivosti, zgornji levi kot, pri čemer je začetna naloga, ne glede na stroške pošiljanja.

Po drugi strani pa najmanjša metoda stroškov vključuje stroške prevoza, medtem ko so naloge opravljene.

- Za razliko od metode Northwest Corner, ta metoda ponuja natančno rešitev, saj upošteva stroške prevoza pri izvajanju dodelitve.

- Metoda minimalnih stroškov je zelo preprosta metoda uporabe.

Lahko vam služi: organizacijski grafikon komercialnega podjetja: položaji in funkcije

- Zelo preprosto in enostavno je izračunati optimalno rešitev s to metodo.

- Metoda minimalnih stroškov je zelo enostavna za razumevanje.

Slabosti

- Za pridobitev optimalne rešitve je treba upoštevati določena pravila. Vendar metoda minimalnih stroškov ne sledi korak za korakom.

- Metoda minimalnih stroškov ne sledi nobenemu sistematičnemu pravilu, kadar je povezava z minimalnimi stroški.

- Metoda minimalnih stroškov omogoča izbiro z opazovanjem osebja, kar bi lahko ustvarilo nesporazume za pridobitev optimalne rešitve.

- Nima možnosti zagotoviti kakršnih koli meril, da bi lahko ugotovili, ali je rešitev, dosežena s to metodo.

- Količine ponudb in zahtev so vedno enake, saj se sčasoma ne razlikujejo.

- Ne upošteva drugih vrst dejavnikov, ki jih je treba dodeliti, ampak le stroške prevoza.

Primer

Koncept metode minimalnih stroškov lahko razumete z naslednjim problemom:

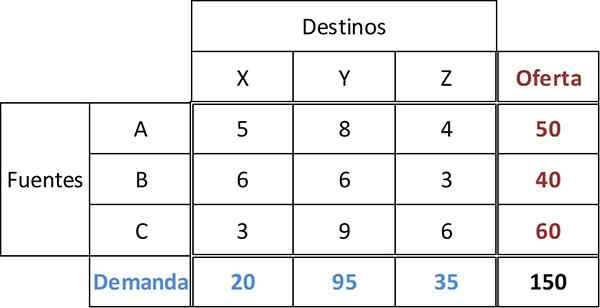
V tej tabeli je ponudba vsakega vira A, B, C 50, 40 in 60 enot. Povpraševanje treh maloprodajnih X, Y, Z, je 20, 95 oziroma 35 enot. Za vse poti se pojavijo stroški prevoza.

Najmanjše stroške prevoza lahko dobite po spodnjih korakih:

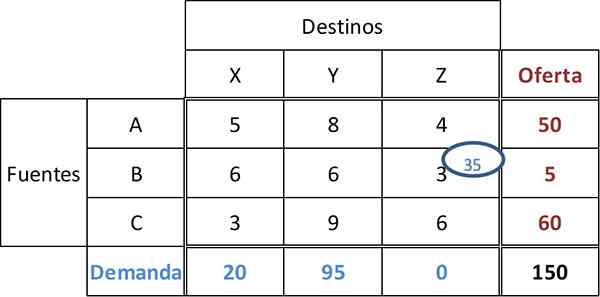
Najnižji stroški v tabeli so 3, s kravato v celicah BZ in CX. Na splošno lahko za pridobitev najboljše začetne rešitve stroške izberete tam, kjer je mogoče dodeliti največji znesek.

Vam lahko služi: plačljivi dokumenti

Zato bo 35 enot dodeljenih celici BZ. Tako je povpraševanje po maloprodaji Z zadovoljno, v Fuente B pa 5 enot pusti.

Pojasnilo metode

Spet so minimalni stroški 3. Zato bo v celični CX dodeljenih 20 enot. Tako je izpolnjena povpraševanje po maloprodaji X, pri čemer je 40 enot v Fuenteu.

Naslednji minimalni stroški so 4. Vendar je povpraševanje po Z že zaključeno. Gre na naslednje minimalne stroške, kar je 5. Tudi povpraševanje po X je bilo že zaključeno.

Naslednji minimalni stroški so 6, z risbo med tremi celicami. Vendar enot ni mogoče dodeliti celicam BX in Cz, ker je povpraševanje po maloprodajni x in z. Potem je 5 enot dodeljenih v celico. Tako je dobava vira B dokončana.

Naslednji minimalni stroški so 8, ki dodelijo 50 enot Cell AY in dopolnjujejo oskrbo z virom.

Naslednji minimalni stroški so 9. 40 enot je dodeljenih v CY celico, s čimer se dokonča povpraševanje in ponudbo vseh destinacij in virov. Rezultat končne naloge je:

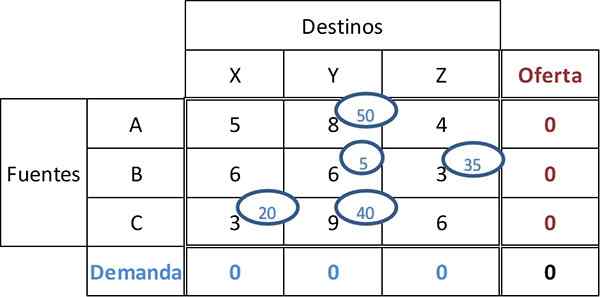
Skupne stroške je mogoče izračunati tako, da pomnožimo zneske, ki jih dodelijo stroški ustreznih celic: Skupni stroški = 50*8 + 5*6 + 35*3 + 20*3 + 40*9 = 955.

Reference

1. Poslovni žargoni (2019). Metoda najmanjših stroškov. Vzeto od: BusinessJargons.com.
2. Svetovanje o nalogah (2019). Pomoč pri dodelitvi metod najmanj stroškov. Vzeto od: AslinmentConsultulty.com.
3. Upravljanje podjetij (2015). Problem prevoza. Vzeto iz: inženirske bachelors.com.
4. Josefina Pacheco (2019). Kakšna je metoda minimalnih stroškov? Splet in podjetja. Vzeto od: Webyempresas.com.
5. Atozmath (2019). Primer metode najmanjših stroškov. Vzet iz: cbom.Atozmath.com.