Eulerjeva metoda za uporabo postopka in vaj

On Eulerjeva metoda Je najosnovnejši in preprost postopki, ki se uporabljajo za iskanje približnih numeričnih rešitev za navadno diferencialno enačbo prvega reda, pod pogojem, da je znan njegov začetni pogoj.

Navadna diferencialna enačba (Edo) je enačba, ki z njegovimi derivati ​​nanaša neznano funkcijo ene same neodvisne spremenljivke.

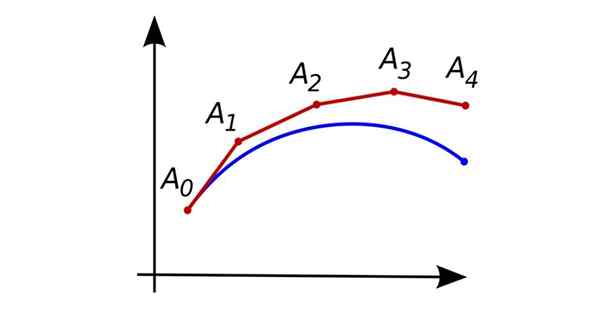
Zaporedni pristopi po Eulerjevi metodi. Vir: Oleg Alexandrov [javna domena]

Če je največji derivat, ki se pojavi v enačbi, ena stopnja, potem je navadna diferencialna enačba prve stopnje.

Najbolj splošen način pisanja enačbe prve stopnje je:

z začetnim pogojem:

x = x₀

y = y₀

[TOC]

Kaj je Eulerjeva metoda?

Ideja Eulerjeve metode je najti numerično rešitev diferencialne enačbe v intervalu med x₀ in x_F .

Prvič, interval v N+1 točkah se ne strinja:

x₀, x₁, x₂, x₃…, X_n

Ki so pridobljeni tako:
x_Yo= x₀+Ih

Kjer je H širina ali korak podintralov:

Večja je število n Rezultat bo natančnejši, vendar bo potrebno večje število točk, da pokrijemo interval, kjer iščemo rešitev in čas računalništva raste.

Z začetnim pogojem je mogoče tudi na začetku poznati derivat:

in '(x_tudi) = f (x_tudi, in_tudi)

Ta derivat predstavlja naklon črte tangenta do krivulje funkcije y (x) natančno na točki:

Ao = (x_tudi, in_tudi)

Nato je na naslednji točki narejena približno napoved vrednosti funkcije y (x):

in (x₁) ≈ in₁

in_1 = in_tudi +(x₁- x_tudi) f (x_tudi, in_tudi) = y_{tudi +} H F (x_tudi, in_tudi)

Naslednja približna točka rešitve, ki bi ustrezala:

Do₁ = (x₁, in₁)

Postopek se ponovi za pridobitev zaporednih točk

Vam lahko služi: logaritmična funkcija: lastnosti, primeri, vaje

Do₂, Do₃…, X_n

Na sliki, prikazani na začetku, modra krivulja predstavlja natančno rešitev diferencialne enačbe, rdeča.

Rešene vaje

Vaja 1

Yo) Bodi diferencialna enačba:

Z začetnim pogojem x = a = 0; in_do= 1

Z uporabo metode Eulerja dobite približno rešitev in V koordinati x = b = 0.5, delitev intervala [a, b] pri n = 5 deli.

Rešitev

Številčni rezultati so povzeti na naslednji način:

Kjer je sklenjeno, da je rešitev in za vrednost 0.5 je 1.4851.

Opomba: Za realizacijo izračunov, ki so bili uporabljeni STATH STUDIO, Brezplačni program brezplačne uporabe.

Vaja 2

Ii) Nadaljevanje z diferencialno enačbo vadbe i) poiščite natančno rešitev in jo primerjajte z rezultatom, pridobljenim z Eulerjevo metodo. Poiščite napako ali razliko med natančnim rezultatom in približnim.

Rešitev

Z začetnim pogojem x = a = 0; in_do= 1
Natančne rešitve ni zelo težko najti. Znano je, da je derivat funkcije sen (x) funkcija cos (x). Zato bo rešitev y (x):

in (x) = sin x + c

Če želite izpolniti začetni pogoj in (0) = 1, mora biti konstanta C vredna 1. Nato natančen rezultat primerjamo s približno:

Ugotovljeno je, da ima v izračunanem intervalu pristop tri pomembne številke natančnosti.

Vaja 3

Iii) Razmislite o diferencialni enačbi in njegovih začetnih pogojih spodaj:

in '(x) =- y²

Z začetnim pogojem x₀ = 0; in₀ = 1

Uporabite metodo Eulerja, da najdete približne vrednosti rešitve in (x) V intervalu x = [0, 1.5. Uporaba koraka H = 0.1.

Rešitev

Eulerjeva metoda je zelo označena za uporabo s preglednico. V tem primeru bomo uporabili preglednico Geogebra, Brezplačni in brezplačni program.

Lahko vam služi: sestavljena sorazmernost: razlaga, tri sestavljene pravila, vaje

V preglednici slike so prikazani trije stolpci (a, b, c) x , Drugi stolpec predstavlja spremenljivko in, in tretji stolpec izpeljan in.

Vrstica 2 vsebuje začetne vrednosti X, In, In .

Vrednost vrednosti 0.1 je postavljena v absolutno pozicijsko celico ($ D $ 4).

Začetna vrednost Y0 je v celici B2 in Y1 v celici B3. Za izračun in₁ Uporablja se formula:

in_1 = in_tudi +(x₁- x_tudi) f (x_tudi, in_tudi) = y_{tudi +} H F (x_tudi, in_tudi)

Ta formula preglednice bi bila številka B3: = B2 + $ D $ 4 * C3.

Podobno bi bil Y2 v celici B4 in njegova formula je prikazana na naslednji sliki:

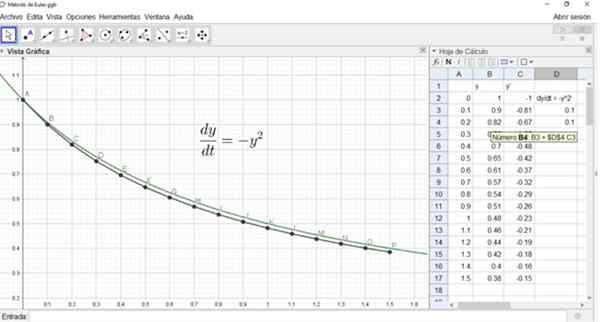
Slika prikazuje tudi graf natančne rešitve in točke A, B, ..., P približne rešitve s pomočjo Eulerjeve metode.

Newton Dynamics in Eulerjeva metoda

Klasično dinamiko je razvil Isaac Newton (1643 - 1727). Prvotna motivacija Leonarda Eulerja (1707 - 1783) za razvoj njegove metode je bila natančno reševanje enačbe Newtonovega drugega zakona v različnih fizičnih situacijah.

Newtonov drugi zakon je pogosto izražen kot sekundarna diferencialna enačba:

Kje x trenutno predstavlja položaj predmeta t. Ta predmet ima maso m in je podvržen sili F. Funkcija F Povezana je z močjo in maso na naslednji način:

 Čeprav je bila načeloma Eulerjeva metoda zasnovana za reševanje diferencialnih enačb prve stopnje, je zlahka razširjena na primer drugega stopnje, saj je enakovredna sistemu dveh prvih enačb enačb.

Lahko vam služi: analitična geometrija

Za uporabo metode Eule so potrebne začetne časovne vrednosti t, hitrost v in položaj x.

Naslednja tabela pojasnjuje, kako lahko v trenutku T2 = T1+ΔT, kjer Δt, v ​​trenutku T2 = T1+ΔT, kjer Δt predstavlja majhno povečanje in ustreza koraku v metodi Eulerja.

Vaja 4

Iv) Eden temeljnih težav pri mehaniki je blok mase M, vezan na vzmet (ali vzmet) elastične konstante K.

Newtonov drugi zakon za to težavo bi bil tak:

V tem primeru bo za poenostavitev vzeta M = 1 in K = 1. Poiščite približne rešitve položaja x In hitrost v Po Eulerjevi metodi v časovnem intervalu [0, π/2], ki razdeli interval v 12 delih.

Vzemite 0 kot začetni trenutek, začetna hitrost 0 in začetni položaj 1.

Rešitev

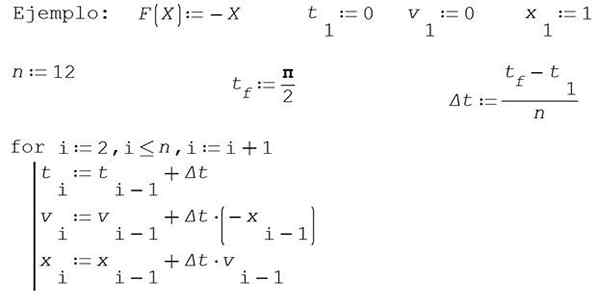
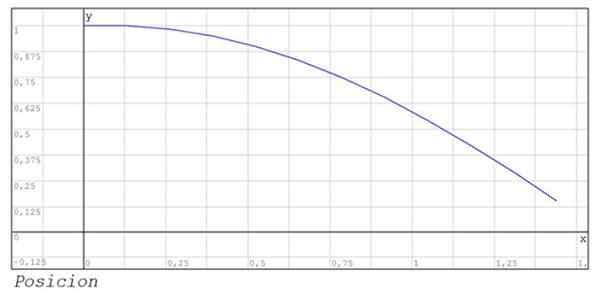
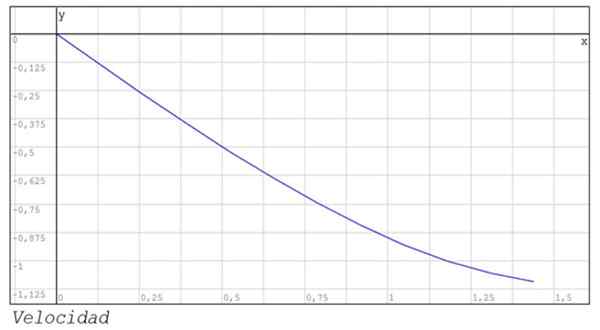
Številčni rezultati so prikazani v naslednji tabeli:

Prikazana sta tudi grafika položaja in hitrost med instami 0 in 1.44.

Predlagane vaje za dom

Vaja 1

Uporabite preglednico za določitev približne rešitve z uporabo Eulerjeve metode za diferencialno enačbo:

in '= -exp (-y) z začetnimi pogoji x = 0, y = -1 v intervalu x = [0, 1]

Začnite s korakom 0,1. Grafirajte rezultat.

Vaja 2

Z uporabo preglednice poiščite numerične rešitve za naslednjo enačbo druge stopnje, kjer in je funkcija neodvisne spremenljivke t.

in "= - 1/y² z začetnim pogojem t = 0; y (0) = 0,5; in '(0) = 0

Poiščite raztopino v intervalu [0,5; 1.0] z uporabo koraka 0,05.

Grafirajte rezultat: in vs t; in 'vs t

Reference

1. Eurlerjeva metoda.Vzeti iz Wikipedije.org
2. Euler Solver. Odvzet od.Smath.com